Логарифмические характеристики. ЛХ звеньев. Логарифмические характеристики основных типовых элементарных звеньев

• Название: Логарифмические характеристики основных типовых элементарных звеньев
• Анкор: Логарифмические характеристики
• Дата: 09.04.2022
• Размер: 132.73 Kb.
• Имя файла: ЛХ звеньев.docx
• Тип: Задача; #457053

Логарифмические характеристики основных типовых элементарных звеньев.

1 . Усилительное звено

ПФ и частотные характеристики усилительного звена: Wр(jω)=K; P(ω)=K; Q(ω)=0; φ(ω)=0.

Wр(jω)=K; P(ω)=K; Q(ω)=0; φ(ω)=0.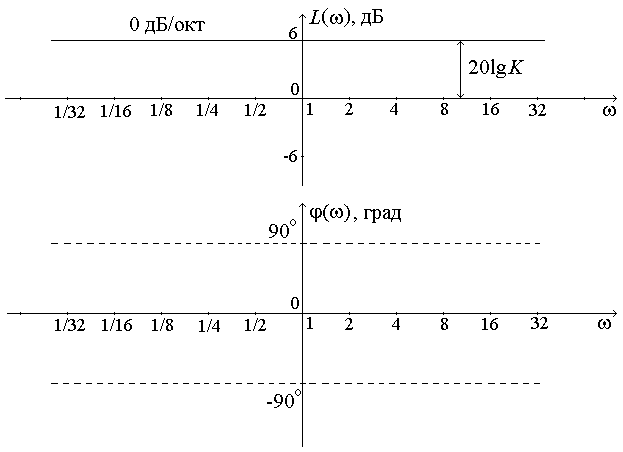





2 . Интегрирующее звено

ПФ и частотные характеристики интегрирующего звена: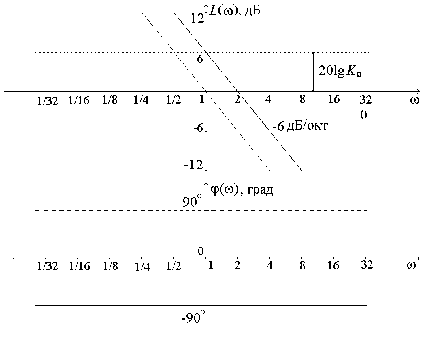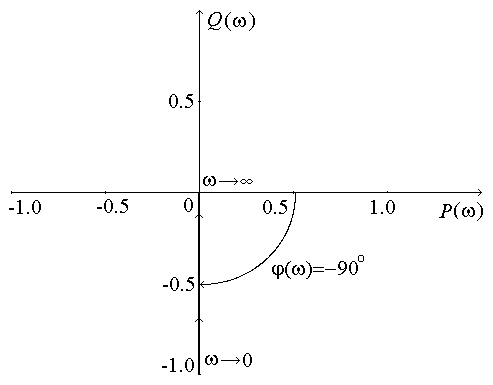



P(ω)=0; φ(ω)=-90.

3. Дифференцирующее звено

ПФ и частотные характеристики дифференцирующего звена:

W_р(jω)=K_дjω; P(ω)=0; Q(ω)= K_дω; φ(ω)=90.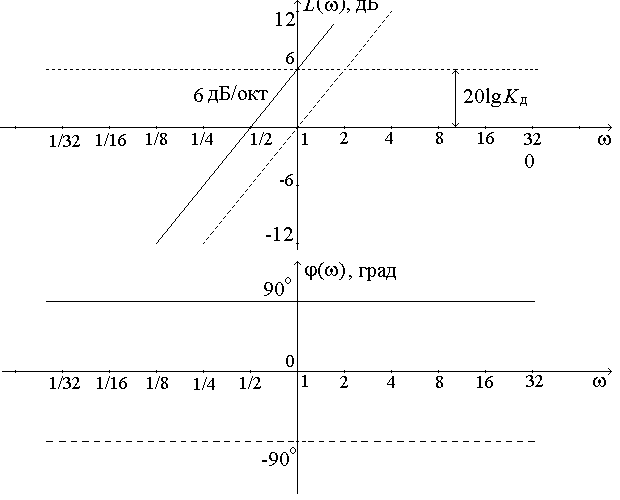





4 . Апериодическое звено

ПФ и частотные характеристики апериодического звена: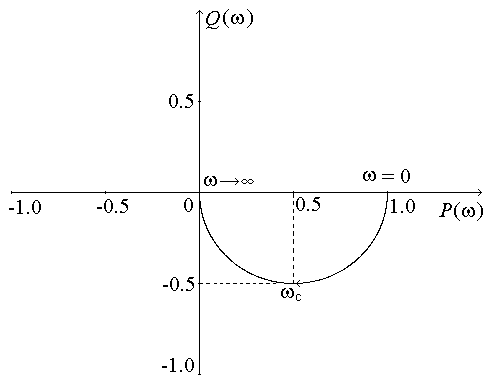








Обе асимптоты пересекаются в точке ω = ω_с = 1/T, где T – постоянная времени апериодического звена. Величина, обратная постоянной времени, – частота сопряжения.

5 . Форсирующее звено

ПФ и частотные характеристики форсирующего звена: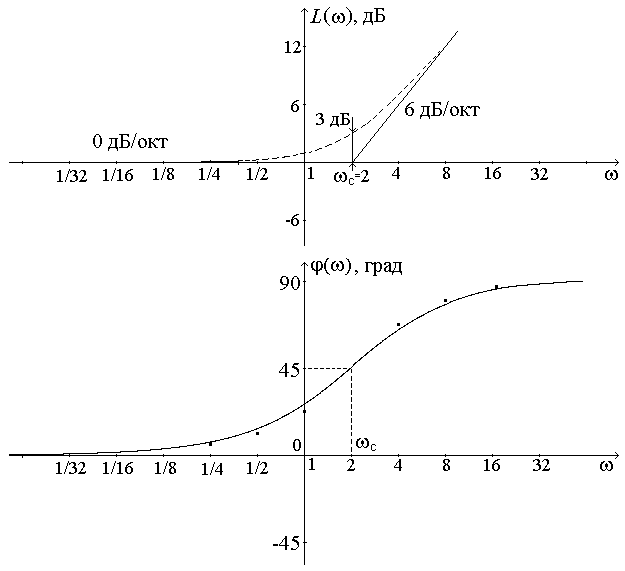







Годограф форсирующего звена похож на годограф дифференцирующего звена, но смещён по Re оси на 1.

6 . Колебательное звено



T – постоянная времени,
ω_о=1/T – частота собственных колебаний звена,
ξ – коэффициент затухания.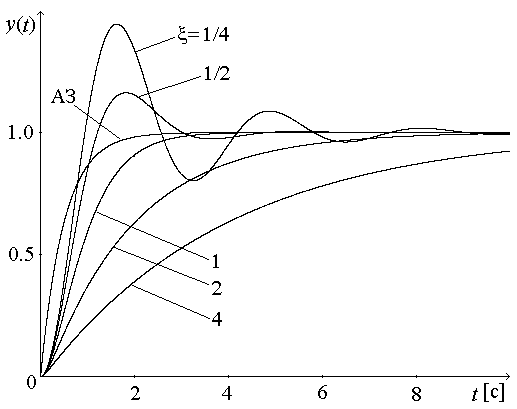


Переходные процессы в колебательном звене (T=0,5с)

Соединение звеньев САР.

Задача по заданной структурной схеме найти передаточную функцию.
Общий метод решения – использование вспомогательных переменных.

1. Последовательное (а)
f(p) – вспомогательная переменная.




2. Параллельное (б)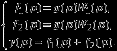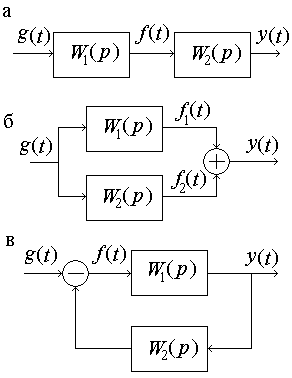



3. Включение звена в цепи отрицательной обратной связи (в)




Если ОС будет положительной, то в знаменателе знак «+» поменяется на знак «–».

Обобщенная структурная схема: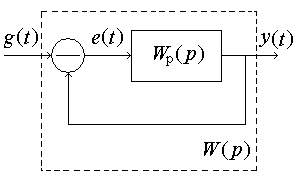



ПФ разомкнутой САР (для построения логарифмических характеристик, а также для анализа качества переходных процессов):



ПФ по ошибке (для анализа точности системы, хотя любая ПФ содержит в себе полную информацию о САР):



ПФ замкнутой САР (для анализа устойчивости и помехоустойчивости):


Уравнения САР: