лекция. Лекция по математике тема_ _Логарифмические уравнения_. Логарифмические уравнения
 Скачать 55.37 Kb. Скачать 55.37 Kb.
|
|
Лекция Тема: Логарифмические уравнения План 1. Определение логарифмического уравнения 2. Решение простейших уравнений 3. Потенцирование. 4. Cведение уравнений к виду log a f(x) = log a g(x) с помощью свойств логарифмов по одному основанию. 5.Уравнения вида Alog a f(x) + Blog b g(x) + C = 0. 6. Введение новой переменной Определение логарифмического уравнения Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Простейшим примером логарифмического уравнения служит уравнение вида loga x = b (где а>0, и а ≠1). Функция у=log a x является возрастающей (или убывающей) на промежутке (0; +∞) и принимает на этом промежутке все действительные значения. По теореме о корне) для любого b это уравнение имеет корень, и только один. Решение простейших уравнений Простейшими логарифмическими уравнениями будем называть уравнения следующих видов: log a x = b, a > 0, a 1. log a f(x) = b, a > 0, a 1. logf(x)b = c,b> 0. Эти уравнения решаются на основании определения логарифма: если logb a = c, то a = bc. Пример 2.1. Решение. Область определения уравнения x > 0. По определению логарифма x = 23, x = 8 принадлежит области определения уравнения. Ответ: x = 8. Уравнения вида logaf(x) = b, a> 0, a ≠ 1. Уравнения данного вида решаются по определению логарифма с учётом области определения функции f(x). Уравнение равносильно следующей системе Обычно область определения находится отдельно, и после решения уравнения f(x) = ab проверяется, принадлежат ли его корни области определения уравнения. Пример 2.2. log3(5х – 1) = 2. Решение: ОДЗ: 5х – 1 > 0; х > 1/5. log3(5х– 1) = 2, log3(5х – 1) = log332, 5х - 1 =9, х = 2. Ответ: 2. Пример 2.3. Решение. Область определения уравнения находится из неравенства 2х2 – 2х – 1 > 0. Воспользуемся определением логарифма:  Применим правила действий со степенями, получим 2х2 – 2х – 1 = 3. Это уравнение имеет два корня х = –1; х = 2. Оба полученные значения неизвестной удовлетворяют неравенству 2х2 – 2х – 1 > 0, т.е. принадлежат области определения данного уравнения, и, значит, являются его корнями. Ответ. х1 = –1, х2 = 2. Уравнения вида logf(x) b = с, b> 0. Уравнения этого вида решаются по определению логарифма с учётом области определения уравнения. Данное уравнение равносильно следующей системе  Чаще всего, область определения логарифмического уравнения находится отдельно, и после решения уравнения (f(x))c = b или равносильного уравнения проверяется, принадлежат ли его корни найденной области. Пример 2.4. logx–19 = 2. Решение. Данное уравнение равносильно системе  Ответ. x = 4. Ответ. x = 4.Потенцирование. Суть метода заключается в переходе от уравнения log a f(x) = log a g(x) к уравнению f(x) = g(x), которое обычно не равносильно исходному. Уравнения вида logaf(x) = logag(x) , а > 0, а 1. На основании свойства монотонности логарифмической функции заключаем, что f(x) = g(x). Переход от уравнения logaf(x) = logag(x) к уравнению f(x) = g(x) называется потенцированием. Нужно отметить, что при таком переходе может нарушиться равносильность уравнения. В данном уравнении f(x) > 0, g(x) > 0, а в полученном после потенцирования эти функции могут быть как положительными, так и отрицательными. Поэтому из найденных корней уравнения f(x) = g(x) нужно отобрать те, которые принадлежат области определения данного уравнения. Остальные корни будут посторонними. Пример 3.1 log3 (x2 – 3x – 5) = log3 (7 – 2x). Решение. Область определения уравнения найдётся из системы неравенств Потенцируя данное уравнение, получаем х2 – 3х – 5 = 7 – 2х, х2 – х – 12 = 0, откуда х1 = –3, х2 = 4. Число 4 не удовлетворяет системе неравенств. Ответ. х = –3. Cведение уравнений к виду log a f(x) = log a g(x) с помощью свойств логарифмов по одному основанию. Если уравнение содержит логарифмы по одному основанию, то для приведения их к виду log a f(x) = log a g(x) используются следующие свойства логарифмов: logb a + logb c = logb (ac), где a > 0; c > 0; b > 0, b 1, logb a – logb c = logb (a/c), где a > 0; c > 0; b > 0, b 1, m logb a = logb a m, где a > 0; b > 0, b 1; mR. Пример 4. 1. log6 (x – 1) = 2 – log6 (5x + 3). Решение. Найдём область определения уравнения из системы неравенств Применяя преобразования, приходим к уравнению log6 (x – 1) + log6 (5x + 3) = 2, log6 ((x – 1)(5x + 3)) = 2, далее, потенцированием, к уравнению (х – 1)(5х + 3) = 36, имеющему два корня х = –2,6; х = 3. Учитывая область определения уравнения, х = 3. Ответ. х = 3. Пример 4.2. Решение. Найдём область определения уравнения, решив неравенство (3x – 1)(x + 3) > 0 методом интервалов. Учитывая, что разность логарифмов равна логарифму частного, получим уравнение log5 (x + 3) 2 = 0. По определению логарифма (х + 3) 2 = 1, х = –4, х = –2. Число х = –2 посторонний корень. Ответ. х = –4. Пример 4. 3. log2 (6 – x) = 2log6 x. Решение. На области определения 0 < x < 6 исходное уравнение равносильно уравнению 6 – x = x2, откуда х = –3, х = 2. Число х = –3 посторонний корень. Ответ. х = 2. Уравнения вида Alog a f(x) + Blog b g(x) + C = 0. Метод потенцирования применяется в том случае, если все логарифмы, входящие в уравнение, имеют одинаковое основание. Для приведения логарифмов к общему основанию используются формулы: Пример 5.1. Решение. Область определения уравнения 1 < x < 2. Используя формулу (3), получим Так как 3 = log28, то на области определения получим равносильное уравнение (2–x)/(x–1) = 8, откуда x = 10/9. Ответ. x = 10/9. Пример 5.2.  Решение. Область определения уравнения x > 1. Приведём логарифмы к основанию 3, используя формулу (4). Пример 5. 3. Решение. Область определения уравнения x > –1, x 0. Приведём логарифмы к основанию 3, используя формулу (2). Умножим обе части уравнения на log 3(x + 1) 0 и перенесем все слагаемые в левую часть уравнения. Получим (log 3(x + 1)–1)2 = 0, откуда log 3(x + 1) = 1 и x= 2. Ответ. x= 2.. Введение новой переменной Рассмотрим два вида логарифмических уравнений, которые введением новой переменной приводятся к квадратным. Уравнения вида Пусть t= logaf(x), tR. Уравнение примет вид t2 + Bt + C = 0. Решив его, найдём х из подстановки t= logaf(x). Учитывая область определения, выберем только те значения x, которые удовлетворяют неравенствуf(x) > 0. Пример 6. 1. lg 2 x – lg x – 6 = 0. Решение. Область определения уравнения – интервал (0; ).Введём новую переменную t = lg x, tR. Уравнение примет вид t 2 – t – 6 = 0. Его корни t1 = –2,t2 = 3. Вернёмся к первоначальной переменной lg x = –2 или lg x = 3, х = 10 –2 или х = 10 3. Оба значения x удовлетворяют области определения данного уравнения (х > 0).Ответ. х = 0,01; х = 1000. Пример 6. 2. Решение. Найдём область определения уравнения  Применив формулу логарифма степени, получим уравнение Так как х < 0, то | x | = –x и следовательно Введём новую переменную t = log3 (–x), tR. Квадратное уравнение t 2 – 4t + 4 = 0имеет два равных корня t1,2 = 2. Вернёмся к первоначальной переменной log3 (–x) = 2, отсюда –х = 9, х = –9. Значение неизвестной принадлежит области определения уравнения. Ответ. х = –9. Уравнения вида Уравнения данного вида приводятся к квадратным умножением обеих частей его на logaf(x) 0. Учитывая, что logaf(x) logf(x)a=1 (свойство logba= 1/ logab), получим уравнение Замена logaf(x)=t, tRприводит его к квадратному At2 + Ct + B = 0. Из уравнений logaf(x)=t1 , logbf(x)=t2 найдем значения x и выберем среди них принадлежащие области определения уравнения: f(x) > 0, f(x) 1. Пример.6.3 Решение. Область определения уравнения находим из условий x+2>0, x+2 1, т.е. x >–2, x –1.Умножим обе части уравнения на log5(x+2) 0, получим Возвращаемся к первоначальной переменной: log5(x+2) = –1, x+2 = 1/5, x = –9/5, log5(x+2) = 2, x+2 = 25, x = 23. Оба корня принадлежат области определения уравнения. Ответ: x= –9/5, x= 23. Упражнения для закрепления материала Решить уравнения 1) 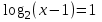 ; 2) ; 2)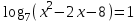 ; 3) ; 3)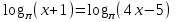 ; ;4) 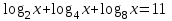 ; 5) ; 5)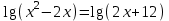 ; ; Контрольные вопросы 1. Сформулировать определение логарифмического уравнения. 2. Назвать основные методы решения логарифмических уравнений Литература 1.Ш.А.Алимов, стр.105-111 2 О.Н.Афанасьева, стор.2753-279 3.А.Г.Мерзляк, стор.202-2 |
