курсовая по теории чисел. Курсовая по теории чисел Магические квадраты. Магические квадраты
 Скачать 327.05 Kb. Скачать 327.05 Kb.
|
§1. Элементарное построение магических квадратов при N = 3; 4П.1.1. Построение магического квадрата при N = 3Из чисел ряда подбираем группы. В каждой группе по n чисел (здесь по 3 числа). Сумма чисел каждой группы должна равняться 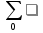 (здесь (здесь 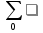 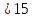 ). ).Готовые группы нужно так разместить в клетках квадрата, чтобы числа группы располагались прямыми рядами: по строкам, по столбцам и по диагоналям. Из 9 чисел натурального ряда можно составить только 8 групп: 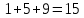 (в этой группе есть пара: (в этой группе есть пара: 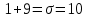 ) )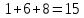 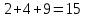 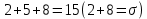 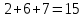 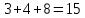 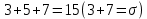 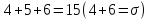 Число 5 входит в 4 группы. Это значит, что клетка для числа 5 находится на пересечении четырех прямых рядов. В квадрате 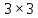 клетки есть только одна такая клетка - средняя (рис. 1.1, а). клетки есть только одна такая клетка - средняя (рис. 1.1, а). Рис. 1.1. а) средняя клетка; б) угловая клетка; в) средняя клетка с края Следовательно, число 5 должно находиться только в центре квадрата и нигде более. Каждые два числа, находящиеся в одной группе и в одном ряду с числом 5, составляют пару. Эти пары располагаются симметрично по отношению к центру квадрата. Поэтому внутренняя структура будет обладать полной центральной симметрией. Каждое четное число ряда встречается в трех группах. Это значит, что четные числа находятся на пересечении трех прямых рядов, то есть в угловых клетках (рис.1.1, б). Каждое из четырех оставшихся нечетных чисел - 1, 3, 7, 9 - входит только в 2 группы. Их место - в средних клетках по краям квадрата (рис. 1.1, в). Если для записи единицы из четырех пригодных клеток выбрать среднюю клетку верхней строки, то для числа 9 оказывается пригодной только одна клетка - средняя на нижней строке. Теперь можно заполнить всю первую строку: 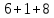 или или 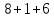 . Это не два варианта, а только вариант и его невариант. . Это не два варианта, а только вариант и его невариант.Числа в нижних угловых клетках определяются диагоналями: 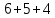 и и 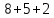 . .Последние два числа 7 и 3 занимают свои места так, как подсказывают группы "5" и "6" (рис. 1.2).  Рис. 1.2. Построение магического квадрата П.1.2. Построение магического квадрата при N = 4Начнём построение магических квадратов 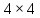 с преобразования немагического квадрата такого же размера, заполненного числами от 1 до 16 в их естественном порядке. Задача решается (в одном только варианте), если поменять местами числа четырех пар: 2 и 15, 3 и 14, 5 и 12, 8 и 9 (рис. 1. 3). с преобразования немагического квадрата такого же размера, заполненного числами от 1 до 16 в их естественном порядке. Задача решается (в одном только варианте), если поменять местами числа четырех пар: 2 и 15, 3 и 14, 5 и 12, 8 и 9 (рис. 1. 3).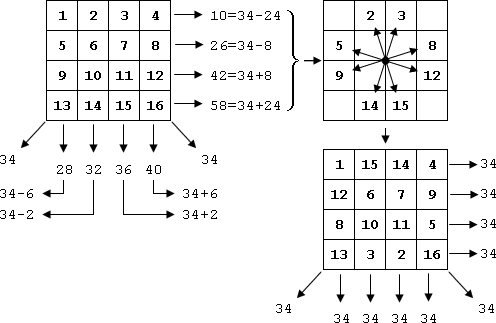 Рис. 1.3. Построение магического квадрата. Полученный таким способом квадрат оказывается магическим, а сам способ известен ещё со времён Дюрера §2. Линейный алгоритм построения магических квадратов нечетного порядкаЛинейный метод построения магических квадратов порядка n имеет вид: 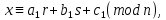 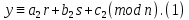 Если 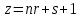 и и 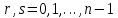 , то , то 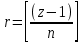 , где []- знак целой части, и , где []- знак целой части, и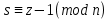 . .Поэтому, формулы (1) можно записать в следующем виде: 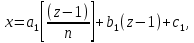 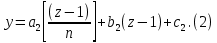 Подставляя в равенства (2) числа 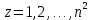 , получаем координаты ряда клеток, часть из которых будет лежать вне основного квадрата. Затем в каждую клетку надо вписать соответствующее число z, заменяя одновременно клетки, лежащие вне основного квадрата, эквивалентными клетками этого квадрата. В результате получим некоторое заполнение клеток основного квадрата числами от 1 до , получаем координаты ряда клеток, часть из которых будет лежать вне основного квадрата. Затем в каждую клетку надо вписать соответствующее число z, заменяя одновременно клетки, лежащие вне основного квадрата, эквивалентными клетками этого квадрата. В результате получим некоторое заполнение клеток основного квадрата числами от 1 до 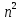 , которое и будет магическим квадратом . , которое и будет магическим квадратом . |
