курсовая по теории чисел. Курсовая по теории чисел Магические квадраты. Магические квадраты
 Скачать 327.05 Kb. Скачать 327.05 Kb.
|
§4. Классические алгоритмы построения магических квадратов нечетного порядкаП.4.1.Индийский (сиамский) методПравила построения магических квадратов произвольного нечетного порядка 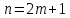 : :Числа от 1 до 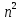 поочередно вписываются в клетки основного квадрата. поочередно вписываются в клетки основного квадрата.Если некоторое правило требует вписать данное число в клетку, лежащую вне основного квадрата, то вместо этого рассматриваемое число вписывается в эквивалентную клетку основного квадрата. Число 1 вписывается в среднюю клетку верхнего ряда, то есть в клетку с координатами 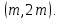 Если число z вписано в клетку с координатами 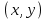 , то следующее число , то следующее число 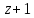 вписывается в клетку с координатами вписывается в клетку с координатами 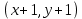 , то есть в клетку, смежную с клеткой , то есть в клетку, смежную с клеткой 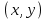 , в направлении восходящей диагонали, при условии, что эта последняя клетка еще свободна от чисел. , в направлении восходящей диагонали, при условии, что эта последняя клетка еще свободна от чисел.Если клетка с координатами 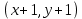 уже занята некоторым числом, то число z+1 вписывается в клетку с координатами уже занята некоторым числом, то число z+1 вписывается в клетку с координатами 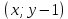 , то есть в клетку, непосредственно примыкающую снизу к клетке , то есть в клетку, непосредственно примыкающую снизу к клетке 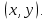 Рассмотрим такой магический квадрат третьего порядка (рис.3.1). Число 1 вписано на основании правил 1 и 3, число 2- на основании правил 4 и 2, число 3- на основании правил 4 и 2, число 4- на основании правил 5 и 2, число 6- на основании правила 4, число 7- на основании правил 5 и 2, число 8-на основании правил 4 и 2, число 9- на основании правил 4 и 2. 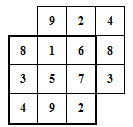 Рис. 3.1. Построение магического квадрата индийским методом З а м е ч а н и е. Из полученного по индийскому методу магического квадрата третьего порядка можно поворотами около центра и отражениями в сторонах получить еще семь других магических квадратов. Без труда проверяется, что этими восемью магическими квадратами исчерпываются все магические квадраты третьего порядка. Сущность индийского метода лучше всего уясняется, если не обращать внимания на правило 2, т. е. если не заменять внешних клеток эквивалентными. При таком упрощении применение алгоритма сводится к заполнению клетки 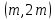 числом 1 и следующих за ней вверх по диагонали клеток числом 1 и следующих за ней вверх по диагонали клеток 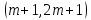 , ,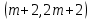 , …, , …,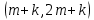 ... числами ... числами 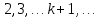 до тех пор, пока не встретится клетка, эквивалентная клетке до тех пор, пока не встретится клетка, эквивалентная клетке 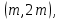 что, очевидно, произойдет при что, очевидно, произойдет при 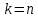 . Под последней из заполненных клеток (это будет клетка . Под последней из заполненных клеток (это будет клетка 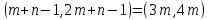 с числом n), т. е. в клетке с числом n), т. е. в клетке 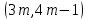 , помещается число , помещается число 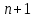 , и с этой клетки начинается новый диагональный ряд, который, как легко видеть, кончится на числе , и с этой клетки начинается новый диагональный ряд, который, как легко видеть, кончится на числе 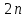 , так что число , так что число 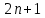 помещается под клеткой с числом помещается под клеткой с числом 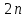 . Следующий диагональный ряд кончится на числе . Следующий диагональный ряд кончится на числе 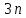 , и т. д. Этот процесс остановится, когда мы дойдем до числа , и т. д. Этот процесс остановится, когда мы дойдем до числа 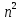 . В результате мы получим n диагональных рядов чисел по n чисел в ряду, составляющих своеобразную "лесенку" (см. рис. 3.2 для n = 3 и n = 5). . В результате мы получим n диагональных рядов чисел по n чисел в ряду, составляющих своеобразную "лесенку" (см. рис. 3.2 для n = 3 и n = 5). Рис. 3.2. Покажем теперь, что клетка построенной "лесенки", содержащая некоторое число 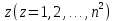 , имеет координаты , имеет координаты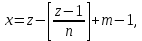 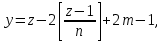 (1) (1)где 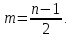 Действительно, для чисел 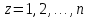 первого диагонального ряда эти формулы дают правильные координаты первого диагонального ряда эти формулы дают правильные координаты 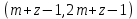 соответствующих клеток (см. выше). Пусть формулы (1) уже доказаны для чисел соответствующих клеток (см. выше). Пусть формулы (1) уже доказаны для чисел 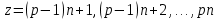 , составляющих , составляющих 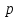 -й диагональный ряд. Тогда, согласно этим формулам, число -й диагональный ряд. Тогда, согласно этим формулам, число 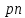 помещается в клетке помещается в клетке 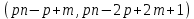 и, следовательно, согласно правилам построения "лесенки", число и, следовательно, согласно правилам построения "лесенки", число 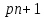 помещается в клетке помещается в клетке 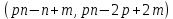 , число , число 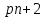 — в клетке — в клетке 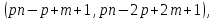 вообще число вообще число 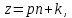 где где 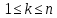 , —в клетке , —в клетке 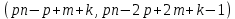 , т. е. в клетке , т. е. в клетке 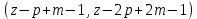 . Поскольку при . Поскольку при 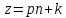 имеет место равенство имеет место равенство 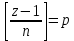 , тем самым доказано, что формулы (1) справедливы и для чисел , тем самым доказано, что формулы (1) справедливы и для чисел 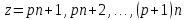 , составляющих , составляющих 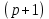 -й ряд. Поэтому, согласно принципу полной математической индукции, формулы (1) справедливы для чисел любого ряда, т. е. для всех чисел от 1 до -й ряд. Поэтому, согласно принципу полной математической индукции, формулы (1) справедливы для чисел любого ряда, т. е. для всех чисел от 1 до 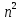 . .Сравнивая доказанные формулы (1) с формулами (2) из п. 2 гл. 1, мы немедленно получаем, что индийский метод является линейным методом с коэффициентами 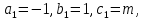 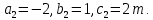 Определитель 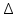 индийского метода равен, очевидно, единице, так что этот метод для любого n удовлетворяет условию M1. Ясно также, что для любого нечетного n он удовлетворяет и условию М2. Далее, так как индийского метода равен, очевидно, единице, так что этот метод для любого n удовлетворяет условию M1. Ясно также, что для любого нечетного n он удовлетворяет и условию М2. Далее, так как 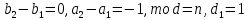 и поэтому условие МЗ сводится к сравнению и поэтому условие МЗ сводится к сравнению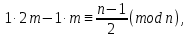 которое очевидным образом удовлетворяется. Наконец, так как 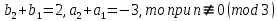 имеет место даже условие М4', а при имеет место даже условие М4', а при 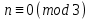 условие М4 сводится к очевидному сравнению условие М4 сводится к очевидному сравнению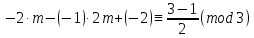 и поэтому также выполнено. Тем самым доказано, что для любого нечетного n индийский метод правилен, т. е. его применение приводит к некоторому магическому квадрату. Индийский метод, не оставляя желать ничего лучшего в отношении простоты и легкости применения, страдает тем недостатком, что для каждого нечетного n он дает лишь один, вполне определенный, магический квадрат. Однако, как мы сейчас покажем, несколько обобщив этот метод, можно получить метод, приводящий, вообще говоря, к n квадратам. П.4.2. Обобщенный индийский методСущество индийского метода состоит в правилах 4, 5, обеспечивающих построение "лесенки". Что же касается правила 3, т. е. требования начинать построение обязательно с клетки 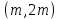 , то оно отнюдь не обязательно. , то оно отнюдь не обязательно.Подставляя в формулы (1) п. 2 общего линейного метода координаты 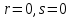 числа 1, мы немедленно получим, что коэффициенты числа 1, мы немедленно получим, что коэффициенты 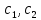 представляют собой координаты клетки, в которую вписано число 1. представляют собой координаты клетки, в которую вписано число 1.Следовательно, варьируя числа 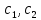 , мы будем менять место числа 1 в квадрате. Сохраняя при этом остальные коэффициенты , мы будем менять место числа 1 в квадрате. Сохраняя при этом остальные коэффициенты 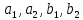 неизменными, мы оставим метод по существу тем же самым. неизменными, мы оставим метод по существу тем же самым.Таким образом, желая исследовать вопрос о возможном обобщении правила 3. индийского метода, мы должны рассмотреть метод вида 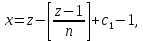 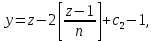 (1) (1)и найти все значения коэффициентов 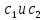 , для которых этот метод правилен. Алгоритм для построения магических квадратов по этому методу состоит из тех же правил 1-5, что и алгоритм индийского метода, с тем лишь отличием, что правило 3 заменяется следующим: , для которых этот метод правилен. Алгоритм для построения магических квадратов по этому методу состоит из тех же правил 1-5, что и алгоритм индийского метода, с тем лишь отличием, что правило 3 заменяется следующим:3'. Число 1 вписывается в клетку с координатами ( 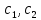 ). ).Метод (1), очевидно, удовлетворяет условиям M1 и М2. Что же касается условия МЗ, то, поскольку 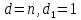 , оно сводится к сравнению , оно сводится к сравнению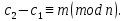 (2) (2)Этому сравнению удовлетворяют n клеток основного квадрата, эквивалентных клеткам "восходящего" диагонального ряда, проходящего через среднюю клетку верхнего ряда. Наконец, если 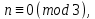 то выполнено условие М4'. Если же то выполнено условие М4'. Если же 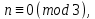 то то 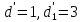 И поэтому условие М4 сводится к сравнению И поэтому условие М4 сводится к сравнению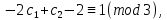 т. е. к сравнению 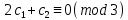 . (3) . (3)С другой стороны, при 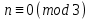 (а значит, при (а значит, при 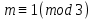 ) из сравнения (2) вытекает сравнение ) из сравнения (2) вытекает сравнение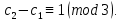 Отсюда и из сравнения (3) следует, что 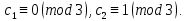 Таким образом, мы получаем следующий окончательный результат: в алгоритме индийского метода начальную клетку, в которую вписывается число 1, можно при 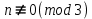 произвольно выбирать среди п клеток, эквивалентным клеткам "восходящего" диагонального ряда, проходящего через среднюю клетку верхнего горизонтального ряда; если же произвольно выбирать среди п клеток, эквивалентным клеткам "восходящего" диагонального ряда, проходящего через среднюю клетку верхнего горизонтального ряда; если же 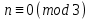 , то эта клетка должна дополнительно обладать тем свойством, что ее первая координата делится на 3 (и тогда вторая при делении на 3 обязательно даст остаток 1 ). , то эта клетка должна дополнительно обладать тем свойством, что ее первая координата делится на 3 (и тогда вторая при делении на 3 обязательно даст остаток 1 ).В частности, за начальную клетку индийского метода можно всегда выбрать среднюю клетку левого вертикального ряда, имеющую координаты 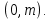 Это видоизменение индийского метода было предложено Лалюбером. Это видоизменение индийского метода было предложено Лалюбером.С помощью обобщенного индийского метода мы получаем либо п квадратов (при 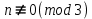 , либо , либо 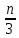 квадратов (при квадратов (при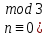 )). )).П.4.3. Метод Москопула (метод коня)Алгоритм последовательного заполнения клеток основного квадрата числами от 1 до 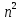 : :Числа от 1 до 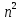 поочередно вписываются в клетки основного квадрата. поочередно вписываются в клетки основного квадрата.Если некоторое правило требует вписать данное число в клетку, лежащую вне основного квадрата, то вместо этого рассматриваемое число вписывается в эквивалентную клетку основного квадрата. Если 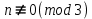 , то начальная клетка, в которую вписывается число 1, выбирается произвольно, если же , то начальная клетка, в которую вписывается число 1, выбирается произвольно, если же 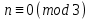 , то за эту клетку принимается средняя клетка нижнего горизонтального ряда, то есть клетка с координатами , то за эту клетку принимается средняя клетка нижнего горизонтального ряда, то есть клетка с координатами 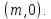 Если некоторое число z вписано в клетку с координатами 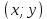 , то число , то число 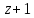 вписывается в клетку с координатами вписывается в клетку с координатами 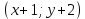 при условии, что эта клетка еще свободна от чисел. магический квадрат линейный четный при условии, что эта клетка еще свободна от чисел. магический квадрат линейный четныйЕсли клетка с координатами 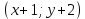 уже занята некоторым числом, то число уже занята некоторым числом, то число 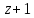 вписывается в клетку с координатами вписывается в клетку с координатами 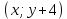 , то есть в клетку, расположенную в том же вертикальном ряду, что и клетка с числом z, но находящуюся на четыре клетки выше. , то есть в клетку, расположенную в том же вертикальном ряду, что и клетка с числом z, но находящуюся на четыре клетки выше.Рассмотрим магический квадрат пятого порядка, построенный по данному методу (рис.3.3). Для изучения метода Москопула мы, как и раньше, отвлечемся от правила 2, т. е. не будем заменять внешние клетки эквивалентными им клетками основного квадрата. Тогда, если мы вписали число 1 в клетку 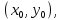 то число 2 мы должны вписать в клетку то число 2 мы должны вписать в клетку 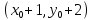 , число 3 — в клетку , число 3 — в клетку 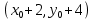 и вообще число и вообще число 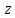 - в клетку - в клетку 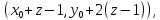 и так до тех пор, пока не встретим клетку, эквивалентную уже занятой. Очевидно, что это произойдет при и так до тех пор, пока не встретим клетку, эквивалентную уже занятой. Очевидно, что это произойдет при 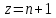 . Поэтому, вписав число n в клетку . Поэтому, вписав число n в клетку 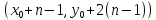 , мы число , мы число 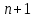 должны вписать в клетку должны вписать в клетку 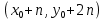 , эквивалентную исходной клетке , эквивалентную исходной клетке 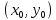 , а - в соответствии с правилом 5 - в клетку , а - в соответствии с правилом 5 - в клетку 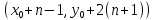 . Дальнейшие вписывания мы должны опять производить по "ходу коня", пока снова не натолкнемся на клетку, эквивалентную уже занятой, что, как легко видеть, произойдет при . Дальнейшие вписывания мы должны опять производить по "ходу коня", пока снова не натолкнемся на клетку, эквивалентную уже занятой, что, как легко видеть, произойдет при 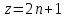 , после чего мы должны совершить "скачек вверх" и т. д. , после чего мы должны совершить "скачек вверх" и т. д.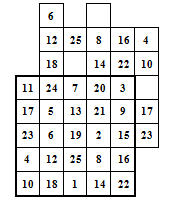 Рис. 3.3. Построение магического квадрата методом Москопула Простой индукцией без труда показывается, что при этом построении число 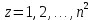 попадает в клетку с координатами попадает в клетку с координатами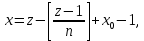 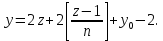 Тем самым доказано, что метод Москопула является линейным методом с коэффициентами 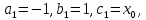 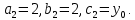 Для этого метода 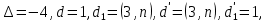 откуда следует, что при 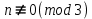 этот метод правилен. Что же касается случая этот метод правилен. Что же касается случая 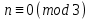 , то для правильности метода должны удовлетворятся сравнения , то для правильности метода должны удовлетворятся сравнения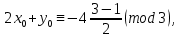 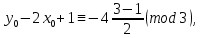 из которых следует, что 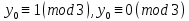 . (1) . (1)Поскольку координаты 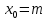 и и 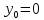 средней клетки нижнего горизонтального ряда удовлетворяют этим соотношениям, то метод Москопула правилен для любого нечетного n. средней клетки нижнего горизонтального ряда удовлетворяют этим соотношениям, то метод Москопула правилен для любого нечетного n.Одновременно мы получаем, что, как и индийский метод, метод Москопула допускает обобщение. Именно, при 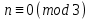 начальную клетку начальную клетку 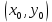 можно выбирать произвольно, лишь бы удовлетворялись сравнения (1). можно выбирать произвольно, лишь бы удовлетворялись сравнения (1).При помощи этого метода получаются 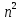 магических квадратов, если магических квадратов, если 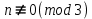 , и , и 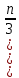 таких квадратов, если таких квадратов, если 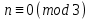 . .При 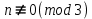 метод Москопула можно видоизменить, заменяя в нем правило 5 правилом 5 индийского метода. метод Москопула можно видоизменить, заменяя в нем правило 5 правилом 5 индийского метода. П.4.4. Метод альфилаПравила построения магического квадрата: Числа от 1 до 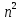 поочередно вписываются в клетки основного квадрата. поочередно вписываются в клетки основного квадрата.Если некоторое правило требует вписать данное число в клетку, лежащую вне основного квадрата, то вместо этого рассматриваемое число вписывается в эквивалентную клетку основного квадрата. Число 1 вписывается в клетку с координатами 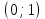 . .Если число z вписано в клетку с координатами 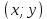 , то число , то число 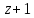 вписывается в клетку с координатами вписывается в клетку с координатами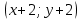 при условии, что эта клетка еще свободна от чисел. при условии, что эта клетка еще свободна от чисел.Если клетка 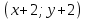 уже занята, то число уже занята, то число 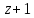 вписывается в клетку с координатами вписывается в клетку с координатами 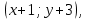 то есть в клетку, получающуюся из клетки z «удлиненным ходом коня». то есть в клетку, получающуюся из клетки z «удлиненным ходом коня».Пример построения магического квадрата пятого порядка (рис.3.4). 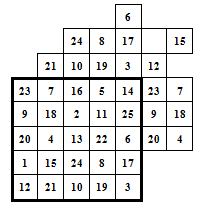 Рис. 3.4. Построение магического квадрата по методу альфила Без труда проверяется (см. аналогичные рассуждения для индийского метода и метода Москопула), что аналитически метод альфила записывается формулами 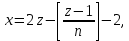 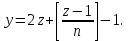 откуда следует, что метод альфила является линейным методом с коэффициентами 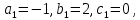 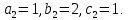 П.4.5. Метод Баше (метод террас)Для построения магического квадрата следует выбрать на плоскости n соседних диагональных рядов, содержащих по n клеток и таких, что средняя клетка каждого ряда принадлежит нисходящей диагонали основного квадрата. Клетки левого верхнего ряда заполняются снизу вверх числами  . Клетки p-го ряда, где . Клетки p-го ряда, где 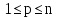 , заполняются числами , заполняются числами 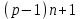 , , 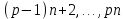 (для (для 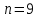 рис.3.5). рис.3.5).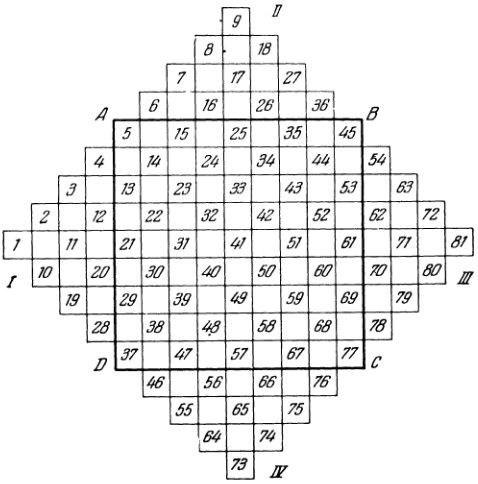 Рис. 3.5. Заполнение магического квадрата по методу Баше Заполненные таким образом клетки частью расположены внутри основного квадрата, частью- вне его, причем внешние клетки образуют по бокам основного квадрата четыре совершенно одинаковых выступа или террасы. Легко видеть, что каждая пустая клетка основного квадрата эквивалентна одной и только одной клетке некоторой террасы. Следовательно, Перенеся клетки террас в основной квадрат, заполним весь основной квадрат числами от 1 до 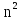 . Оказывается, что получающийся таким образом числовой квадрат является магическим. . Оказывается, что получающийся таким образом числовой квадрат является магическим.На рис. 3.5 образовавшиеся при заполнении клеток террасы обозначены римскими цифрами I, II, III и IV. Для построения магического квадрата террасу I следует передвинуть параллельно самой себе так, чтобы линия AD совпала с линией ВС, террасу II передвинуть так, чтобы линия АВ совпала с линией DC, террасу III -так, чтобы линия ВС совпала с линией AD и, наконец, террасу IV - так, чтобы линия DC совпала с линией АВ. Получающийся в результате магический квадрат изображен на рис. 3.6. 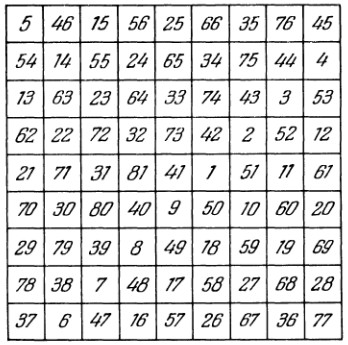 Рис. 3.6. Магический квадрат по методу Баше Для доказательства правильности метода Баше мы сдвинем второй сверху диагональный ряд вдоль его направления на п клеток вверх. Ясно, что при этом каждая клетка ряда заменится ей эквивалентной. Далее подобным же образом сдвинем третий ряд на 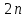 клеток вверх и вообще клеток вверх и вообще 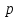 -й ряд, где -й ряд, где 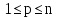 , сдвинем на , сдвинем на 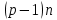 клеток вверх. Без труда проверяется, что получившаяся таким образом система клеток аналитически определяется формулами клеток вверх. Без труда проверяется, что получившаяся таким образом система клеток аналитически определяется формулами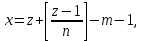 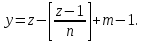 Отсюда вытекает, что метод Баше является линейным методом с коэффициентами 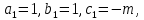 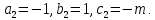 Для этого метода 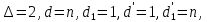 Следовательно, проверки требует лишь первое сравнение условия МЗ и второе сравнение условия М4. В данном случае эти сравнения имеют вид 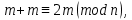 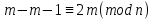 и очевидным образом справедливы. Тем самым доказано, что метод Баше правилен для любого нечетного n. По форме алгоритм метода Баше отличается от ранее рассмотренных алгоритмов (индийского, Москопула и альфила). Однако, как легко видеть, он приводит к тому же магическому квадрату, что и алгоритм, для которого правила 1, 2 и 4 совпадают с правилами индийского метода, а правила 3 и 5 формулируются следующим образом: 3. Число 1 вписывается в клетку с координатами 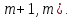 5. Если клетка с координатами 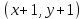 уже заполнена, то число уже заполнена, то число 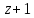 вписывается в клетку, имеющую координаты 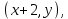 т. е. в клетку, сдвинутую на две клетки вправо. т. е. в клетку, сдвинутую на две клетки вправо.Таким образом, метод Баше принадлежит к тому же типу алгоритмических методов, что и рассмотренные ранее методы. П.4.6. Классические алгоритмические методы с общей точки зренияВсе рассмотренные алгоритмические методы имеют друг с другом много общего. Все они описываются пятью правилами, из которых первые два для всех методов одинаковы, третье описывает возможные координаты 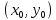 начальной клетки, в которую вписывается число 1, четвертое указывает координаты начальной клетки, в которую вписывается число 1, четвертое указывает координаты 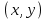 клетки, в которую вписывается число клетки, в которую вписывается число 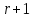 , при условии, что число , при условии, что число 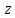 вписано в клетку вписано в клетку 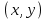 и что клетка и что клетка 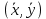 еще свободна от чисел, и, наконец, пятое правило указывает координаты еще свободна от чисел, и, наконец, пятое правило указывает координаты 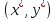 клетки, в которую вписывается число клетки, в которую вписывается число 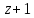 , если клетка , если клетка 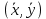 уже оказалась занятой. При этом для любых уже оказалась занятой. При этом для любых 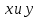 величины величины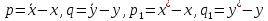 имеют одно и то же постоянное значение. Такого рода алгоритмы построения магических квадратов мы будем называть классическими, а числа 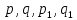 - параметрами данного классического алгоритма. - параметрами данного классического алгоритма.Для индийского метода 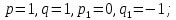 для метода Москопула 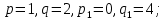 для метода альфила 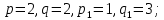 для метода Баше 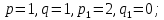 По индукции легко проверяется (см. аналогичные рассуждения для конкретных методов), что классический метод с параметрами 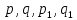 аналитически выражается формулами аналитически выражается формулами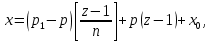 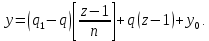 Таким образом, любой классический алгоритмический метод построения магических квадратов равносилен линейному методу с коэффициентами (1) 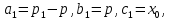 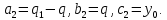 (1) (1)Обратно, любой линейный метод равносилен классическому алгоритмическому методу с параметрами 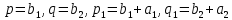 и начальной клеткой 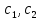 . .Подставляя выражения (1) в условия M1-М4 правильности общего линейного метода, мы получим следующие условия: А1. Число 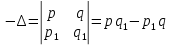 взаимно просто с n. А2. Числа 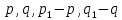 взаимно просты с n. взаимно просты с n.A3. Имеют место сравнения 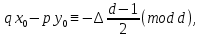 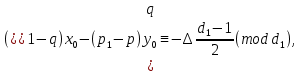 где 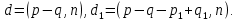 A4. Имеют место сравнения 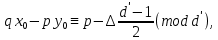 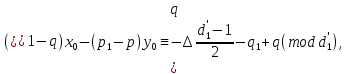 где 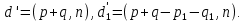 Аналогично условия МЗ' и М4' переходят в условия: A3'. Числа 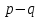 и и 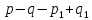 взаимно просты с n. взаимно просты с n.А4'. Числа 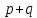 и и 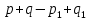 взаимно просты с n. взаимно просты с n.Из всего сказанного следует, что для правильности классического алгоритмического метода с параметрами 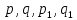 достаточно выполнение условий A1, А2, A3 (или A3') и А4 (или А4') . достаточно выполнение условий A1, А2, A3 (или A3') и А4 (или А4') .ВыводВ своей работе я занималась исследованием одного из вопросов математики, волновавших многих великих людей, - магических квадратов. Хотя магические квадраты не получили широкого распространения в науке и технике, они вдохновили многих людей на изучение математики и внесли свой вклад в развитие других разделов математики. Ближайшие родственники магических квадратов, латинские квадраты, нашли многочисленные применения как в математике, в шифровании текста. Выполняя эту работу, я многое узнала о магических квадратах, но все же, есть еще много, нерассмотренного мною. Я получила огромное удовольствие от этой работы и считаю, что еще слишком рано ставить "точку" в моей работе, и я буду искать дальнейшие исследования того, как заполнить магические квадраты. Список литературыГуревич Е.Я. Тайна древнего талисмана. – М.: Наука, 1969. -150 с. Постников М.М. Магические квадраты. – М.: Наука, 1964. - 84 с. http://xreferat.ru/54/540-1-magicheskie-kvadraty.html http://nsportal.ru/ap/drugoe/magicheskie-kvadraty http://bigor.bmstu.ru |
