курсовая по теории чисел. Курсовая по теории чисел Магические квадраты. Магические квадраты
 Скачать 327.05 Kb. Скачать 327.05 Kb.
|
§3. Условия правильности линейного методаЧтобы линейный метод, выраженный формулами (1) п. 2, был правильным, необходимо в первую очередь, чтобы эти формулы устанавливали взаимно однозначное соответствие между координатами 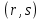 чисел от 1 до чисел от 1 до 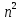 и координатами и координатами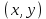 клеток основного квадрата, т. е. чтобы для любых координат клеток основного квадрата, т. е. чтобы для любых координат 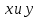 из этих формул можно было однозначно найти соответствующие координаты из этих формул можно было однозначно найти соответствующие координаты 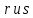 . Но решая по известным правилам сравнения (1) п. 2 относительно . Но решая по известным правилам сравнения (1) п. 2 относительно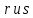 , мы получим сравнения , мы получим сравнения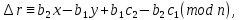 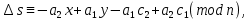 (1) (1)где 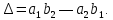 Пусть выполнено следующее условие: M1. Определитель 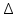 взаимно прост с n. взаимно прост с n.Тогда для любых х и у сравнения (1) однозначно определяют координаты 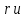 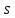 (следует иметь ввиду, что, по определению, эти координаты принадлежат полной системе (2) п. 1 наименьших неотрицательных вычетов по модулю n). Таким образом, при выполнении условия M1. формулы (1) п.2 устанавливают взаимно однозначное соответствие между числами от 1 до (следует иметь ввиду, что, по определению, эти координаты принадлежат полной системе (2) п. 1 наименьших неотрицательных вычетов по модулю n). Таким образом, при выполнении условия M1. формулы (1) п.2 устанавливают взаимно однозначное соответствие между числами от 1 до 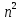 и клетками основного квадрата. и клетками основного квадрата.Рассмотрим теперь следующее условие: М2. Коэффициенты 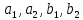 взаимно просты с n. взаимно просты с n.Оказывается, что при выполнении условия М2 требование магичности выполняется по отношению ко всем вертикальным и горизонтальным рядам, т. е. сумма чисел каждого вертикального и каждого горизонтального ряда равна 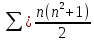 Действительно, для всех клеток некоторого, скажем, горизонтального ряда координата 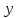 одна и та же, а координата х пробегает полную систему вычетов по модулю n. Так как числа одна и та же, а координата х пробегает полную систему вычетов по модулю n. Так как числа 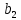 и и 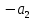 по условию взаимно просты с n, то левые части сравнений (1), каждая в отдельности, также пробегают полную систему вычетов. Поэтому полную систему вычетов будут пробегать как координата r, так и координата s (ибо по условию М1 определитель по условию взаимно просты с n, то левые части сравнений (1), каждая в отдельности, также пробегают полную систему вычетов. Поэтому полную систему вычетов будут пробегать как координата r, так и координата s (ибо по условию М1 определитель 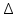 взаимно прост с n). Таким образом, для чисел рассматриваемого ряда координаты г и s принимают по одному разу каждое из значений взаимно прост с n). Таким образом, для чисел рассматриваемого ряда координаты г и s принимают по одному разу каждое из значений 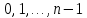 . Следовательно, суммы R и S этих координат равны каждая числу . Следовательно, суммы R и S этих координат равны каждая числу 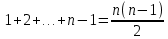 . C другой стороны, сумма всех чисел данного ряда равна, очевидно, числу . C другой стороны, сумма всех чисел данного ряда равна, очевидно, числу 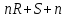 . Поэтому для завершения доказательства остается лишь заметить, что . Поэтому для завершения доказательства остается лишь заметить, что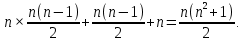 Для вертикальных рядов рассуждение аналогично (меняется координата у, а координата х остается постоянной). Таким образом, остается найти лишь условия магичности обеих диагоналей ("восходящей", соединяющей левый нижний угол с правым верхним, и "нисходящей", соединяющей левый верхний угол с правым нижним). Для клеток восходящей диагонали имеет место равенство 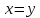 , и поэтому , и поэтомукоординаты чисел, находящихся в клетках этой диагонали, определяются из сравнений 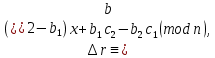 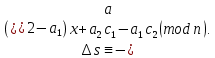 Так как число 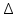 взаимно просто с n, то существует такое число взаимно просто с n, то существует такое число 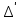 , что , что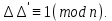 Умножая выписанные выше сравнения на это число, мы получим, что 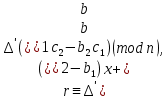 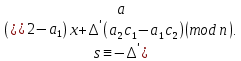 (2) (2)Таким образом, координаты r и s чисел восходящей диагонали представляют собой вычеты значений, принимаемых левыми частями сравнений (2), когда х пробегает полную систему вычетов 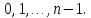 Следовательно, суммы R и S этих координат выражаются формулами Следовательно, суммы R и S этих координат выражаются формулами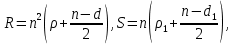 где 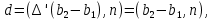 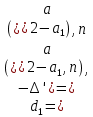 а 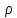 и и 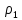 представляют собой наименьшие неотрицательные вычеты чисел представляют собой наименьшие неотрицательные вычеты чисел 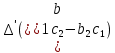 и и 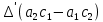 по модулям по модулям 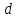 и и 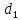 соответственно. соответственно.Требование магичности заключается в том, что сумма 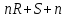 всех чисел всех чиселвосходящей диагонали равна 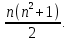 Следовательно, должно иметь место равенство Следовательно, должно иметь место равенство 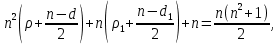 т. е. равенство 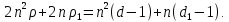 Последнее равенство возможно только при 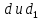 нечетных и, как легко видеть, нечетных и, как легко видеть,будет заведомо выполнено, если 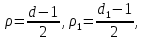 т. е. если будут иметь место сравнения 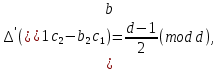 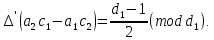 Умножив эти сравнения на 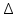 , мы придем к следующему условию: , мы придем к следующему условию:МЗ. Имеют место сравнения 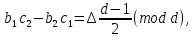 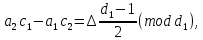 где  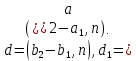 По доказанному при выполнении условия МЗ восходящая диагональ удовлетворяет условию магичности. Заметим, что при 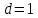 или при или при 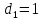 соответствующее сравнение из условия МЗ удовлетворяется автоматически. Отсюда, в частности, следует, что условие МЗ будет заведомо выполнено, если соответствующее сравнение из условия МЗ удовлетворяется автоматически. Отсюда, в частности, следует, что условие МЗ будет заведомо выполнено, если 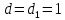 , т. е. если выполнено следующее условие: , т. е. если выполнено следующее условие:МЗ'. Числа 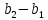 и и 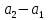 взаимно просты с n. взаимно просты с n.Для нисходящей диагонали 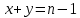 , и поэтому ее клетки заполнены числами, координаты которых определяются из сравнений , и поэтому ее клетки заполнены числами, координаты которых определяются из сравнений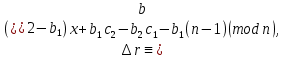 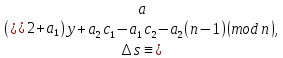 т. е. из сравнений 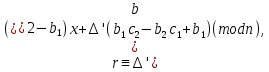 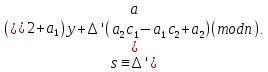 Отсюда, как и выше мы приходим к условию М4 Имеют место сравнения 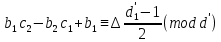 , ,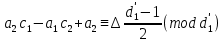 , ,где 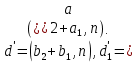 и к следующему утверждению: при выполнении условия М4 нисходящая диагональ удовлетворяет условию магичности. Условие М4 будет заведомо выполнено, если имеет место следующее условие: М4'. Числа 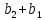 и и 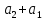 взаимно просты с n. взаимно просты с n.Резюмируя все сказанное, мы получаем окончательный результат: при выполнении условий M1, М2, МЗ (или МЗ') и М4 (или М4') линейный метод (1) п. 2 правилен. Это утверждение дает лишь достаточные условия правильности линейного метода. Заметим в заключение, что условия M1 и М2 непротиворечивы только для нечетного n. Действительно, если n четно, то, согласно условию М2, числа 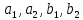 должны быть нечетны, и поэтому определитель 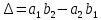 , как разность двух нечетных чисел, должен быть четным, что в силу условия M1 невозможно. , как разность двух нечетных чисел, должен быть четным, что в силу условия M1 невозможно.Таким образом, правильные методы (или по крайней мере методы, удовлетворяющие условиям M1-М4) могут существовать лишь при нечетном n. Примеры таких методов для любого нечетного n я укажу в следующей главе. |
