курсовая по теории чисел. Курсовая по теории чисел Магические квадраты. Магические квадраты
 Скачать 327.05 Kb. Скачать 327.05 Kb.
|
 Министерство просвещения Российской Федерации Федеральное Государственное Образовательное Учреждение Высшего Образования МОСКОВСКИЙ ПЕДАГОГИЧЕСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Институт математики и информатики Курсовая работа по дисциплине «Теория чисел» на тему: «Магические квадраты». Выполнила студентка 3 курса 302 группы Киселева Екатерина Преподаватель: Иконникова Т.К. Оглавление1 Министерство просвещения Российской Федерации 1 Федеральное Государственное Образовательное Учреждение Высшего Образования 1 МОСКОВСКИЙ ПЕДАГОГИЧЕСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ 1 Институт математики и информатики 1 Введение 4 §1. Элементарное построение магических квадратов при N = 3; 4 6 П.1.1. Построение магического квадрата при N = 3 6 П.1.2. Построение магического квадрата при N = 4 8 §2. Линейный алгоритм построения магических квадратов нечетного порядка 8 §3. Условия правильности линейного метода 10 §4. Классические алгоритмы построения магических квадратов нечетного порядка 16 П.4.1.Индийский (сиамский) метод 16 П.4.2. Обобщенный индийский метод 19 П.4.3. Метод Москопула (метод коня) 22 П.4.4. Метод альфила 25 П.4.5. Метод Баше (метод террас) 27 П.4.6. Классические алгоритмические методы с общей точки зрения 30 Вывод 33 Список литературы 34 Введение 3 §1. Элементарное построение магических квадратов при N = 3; 4 5 П.1.1. Построение магического квадрата при N = 3 5 П.1.2. Построение магического квадрата при N = 4 7 §2. Линейный алгоритм построения магических квадратов нечетного порядка 8 §3. Условия правильности линейного метода 9 §4. Классические алгоритмы построения магических квадратов нечетного порядка 14 П.4.1.Индийский (сиамский) метод 14 П.4.2. Обобщенный индийский метод 18 П.4.3. Метод Москопула (метод коня) 20 П.4.4. Метод альфила 23 П.4.5. Метод Баше (метод террас) 25 П.4.6. Классические алгоритмические методы с общей точки зрения 28 Вывод 31 Список литературы 32 ВведениеМагический квадрат — это квадратная таблица 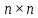 , заполненная , заполненная 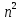 числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный целыми числами от 1 до числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный целыми числами от 1 до 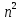 . Магический квадрат называется ассоциативным или симметричным, если сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна . Магический квадрат называется ассоциативным или симметричным, если сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна 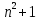 . .Магический квадрат – древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (около 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы (рис. 0.1, а), и эти знаки известны под названием ло-шу и равносильны магическому квадрату (рис. 0.1, б). 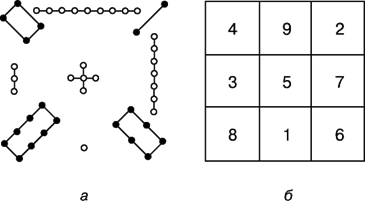 Рис. 0.1. а) таинственные иероглифы на панцире черепахи; б) магический квадрат В XI в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 в. магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера (рис. 0.2), изображенный на его знаменитой гравюре "Меланхолия I".  Рис. 0.2. Магический квадрат А.Дюрера. Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки. Магическим квадратам приписывали различные мистические свойства. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты. В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры. |
