макромодели экономической динамики. Макроэкономические модели равновесной динамики
 Скачать 472.32 Kb. Скачать 472.32 Kb.
|
|
Тема 3. Модели и математические методы анализа микроэкономических процессов и систем. Цель проверки: формирование способности собрать и проанализировать исходные данные, необходимые для расчета экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов (ПК-1). Проверяемые компетенции: ПК-1. Задания реферативного типа. Содержание реферативных заданий 1. Модели поведение потребителей. 2. Модели поведение производителей. 3. Модели взаимодействия потребителей и производителей. Критерии и шкалы оценивания: - оценка «отлично» выставляется, если даны обоснованные, логично выстроенные ответы, отражающие знание обучающегося как основной, так и дополнительной литературы по данной дисциплине; владение обучающегося научной терминологией. Обучающийся демонстрирует умение использовать теоретические знания при трактовке и объяснении практических ситуаций, представлять свою профессиональную позицию; - оценка «хорошо» выставляется, если ответы недостаточно полно обоснованы, отражают знание обучающегося основной литературы по дисциплине, владение обучающегося научной терминологией. Объяснение и трактовка практических ситуаций поверхностны, профессиональная позиция недостаточно ясная; - оценка «удовлетворительно» выставляется, если ответы поверхностные, обучающийся демонстрирует необходимый минимум знаний по дисциплине. Фрагментарное использование теоретических знаний при трактовке и объяснении практических ситуаций, несформированность собственной профессиональной позиции; - оценка «неудовлетворительно» выставляется, если ответы демонстрируют незнание или минимальное знание обучающимся основной литературы по дисциплине. Неумение использовать теоретические знания при трактовке и объяснении практических ситуаций, несформированность собственной профессиональной позиции. Разработка и исследование макромоделей экономической динамики… В условиях равновесия и неравновесия, конкурентной экономики, монополии, олигополии, сочетания различных форм собственности Функции спроса и предложения являются основными составляющими модели рынка товаров, поскольку они - по предположению - представляют собой решения оптимизационных задач, которые возникают перед участниками (покупателями и товаропроизводителями). Пересечение графиков функций спроса и предложения происходит в точке равновесия (рис. 1); соответствующая этой точке цена Р = Ре называется равновесной. Если цена на рынке выше равновесной, то предложение превышает спрос и возникает затоваривание. В этой ситуации товаропроизводители (продавцы) многих видов товаров готовы пойти на снижение цены с целью привлечения большего числа покупателей (например, если речь идет о скоропортящихся продуктах: свежей рыбе и пр.). Следовательно, при значениях цены выше равновесной происходит давление на нее в сторону уменьшения. 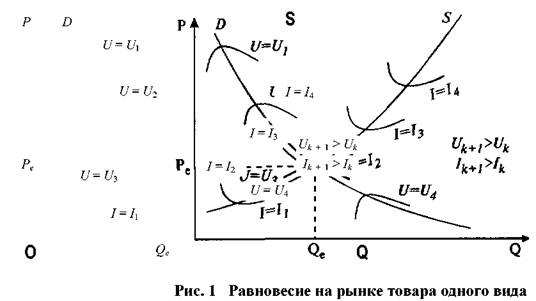 Если же цена на рынке ниже равновесной, то спрос превышает предложение и товар является дефицитным. В этой ситуации часть покупателей готова заплатить за товар более высокую цену, но снизить риск и с уверенностью приобрести товар (например, если покупатели образуют очередь, то стоящие в конце ее могут оказаться без товара). Таким образом, при значениях цены ниже равновесной происходит давление на нее в сторону увеличения. Эти две тенденции приводят к тому, что на рынках многих видов товаров, как правило, устанавливается равновесие, при котором спрос равен предложению. В силу свойств кривых спроса и предложения равновесное решение является устойчивым в том смысле, что если цена строго фиксирована и равна равновесной Р = Ре, то товаропроизводитель, максимизируя прибыль, поставляет на рынок товар в количестве S(Pe) = Qe; одновременно потребитель, стремясь максимизировать полезность, предъявляет спрос D(Pe) = Qe. Итак, при установлении на рынке совершенной конкуренции равновесной цены объем товаров, предлагаемый товаропроизводителем и доставляющий ему максимум прибыли при данной цене, в точности равен спросу потребителя. Равновесные модели различных рынков широко используются при экономическом анализе не только в учебной литературе, но и в практике конкретных экономических исследований. При этом очень часто для обоснования управленческих решений, выводов и рекомендаций, вызванных необходимостью изменения тех или иных условий, служит анализ соответствующего смещения точки равновесия теоретической модели. Отметим, однако, что равновесное решение достигается далеко не всегда и не на всех рынках. По-этому модели процессов установления равновесия (цен, объемов продаж, национального дохода и т.д.) находятся в центре внимания исследователей с начального периода применения формализованных методов в экономике до наших дней. Динамические неравновесные модели рынка используются для анализа изменения переменных (цена, спрос, предложение) во времени в случае, когда цена в начальный момент отличается от равновесной. При этом процесс установления равновесной цены может быть описан различными моделями при использовании одних и тех же функций спроса Q = D(P) и предложения Q = S(P). Различают два подхода – непрерывный, в котором динамика процесса описывается дифференциальным уравнением и дискретный, когда переменные на промежутке времени [t, t + 1) принимаются неизменными (в последнем случае последовательным интервалам времени [t, t + 1) соответствуют значения цены Рt, спроса Dt и предложения St). В зависимости от используемых гипотез в дискретной модели динамики цен происходит либо запаздывание предложения – в этом случае приходим к итерационному процессу либо запаздывание спроса – в этом случае получаем итерационный процесс В обоих случаях при использовании второго подхода соответствующий итерационный процесс час-то изображается на плоскости QOP в виде паутины, которая намотана на кривые спроса и предложения. Поэтому различные дискретные модели динамики цен получили общее название: паутинообразные модели. Значение дискретных паутинообразных моделей указанного выше вида определяется тем, что в них более последовательно, чем в непрерывных моделях, отражаются процедуры принятия решений. 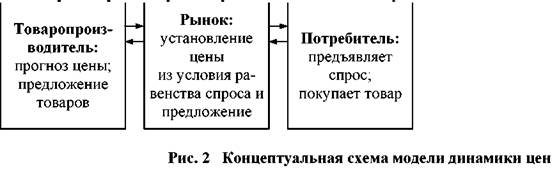 процесса динамики цен включает взаимодействие трех подсистем, которые можно условно назвать товаропроизводитель, потребитель и рынок (рис. 2). Паутинообразная модель (модель А), которая сводится к итерационному процессу, также вписывается в схему 2 (здесь спрос отстает от предложения на один период). Модель А – одна из исторически первых динамических моделей рынка, отражающих поведение участников. Она служит хорошей иллюстрацией применения метода моделирования при анализе экономических процессов. Значение модели А определяется еще и тем, что многие современные модели динамики цен, а также динамические модели макроэкономики приводят к паутинообразному процессу. Рассмотрим гипотезы, которые лежат в основе этой модели. Гипотеза 1. Товаропроизводитель, принимая решение об объеме предложения, ориентируется на цену предыдущего периода. Эта гипотеза означает, что товаропроизводитель прогнозирует цену следующего периода. Правда, прогноз здесь очень примитивный, опирается на такую логическую схему: сегодня цена была Рt; если и завтра она будет равна Рt, то я получу максимальную выгоду при продаже товара в количестве S(Pt). Гипотеза 2. Рынок всегда находится в состоянии локального равновесия. Эту гипотезу можно трактовать, по Вальрасу, следующим образом. Вместо абстрактного, неодушевленного понятия рынок последний выступает в виде некоего человека-аукциониста, распоряжающегося на реальном рынке. Этот аукционист сначала устанавливает произвольные цены на товары, после чего участники рынка совершают условные сделки и сообщают об их результате аукционисту. Если спрос на некоторый товар оказался больше (меньше) предложения, то аукционист меняет первоначальные цены, поднимая (понижая) цену этого товара. Окончательные сделки совершаются лишь после достижения равновесия. Другая трактовка этой гипотезы состоит в том, что задачей аукциониста является установление максимальной цены, при которой весь товар, поставляемый на рынок товаропроизводителем, находит покупателя. Формально эти две гипотезы означают выполнение следующих условий: объем предложения на рынке St + 1 в каждый период времени t + 1 определяется значением цены предыдущего периода при помощи функции предложения St + 1 = S(Pt); на рынке в каждый период t + 1 устанавливается равновесная цена Рt + 1, причем эта цена является решением уравнения D(Pt + 1) = St + 1; потребитель предъявляет спрос, который при цене Рt + 1 в каждый момент времени равен предложению St + 1, вследствие чего потребитель покупает все, что ему предложено. Принятое в модели А взаимодействие подсистем потребитель, товаропроизводитель и рынок может быть представлено в виде блок-схемы, изображенной на рис. 3. Использование монотонных функций спроса и предложения позволяет построить последовательность цен Pt, где t – номер шага во времени. Таким образом, сформулированные две гипотезы приводят к итерационному процессу, где спрос запаздывает от предложения на один период. Динамика цены (а также спроса и предложения) в рамках данной модели может быть изображена в виде кривой, которую называют либо паутиной, либо спиралью. Характер динамики цен зависит в данной модели от отношения угловых коэффициентов функций спроса и предложения. Поэтому теоретически равновесное решение паутинообразной модели может быть и неустойчивым. В основе модели с запаздыванием предложения (модель В, рис. 4) лежат следующие гипотезы. Гипотеза 1. При определении объема предложения в каждый период времени товаропроизводитель ориентируется на спрос в предыдущий период. Эта гипотеза приводит к росту (снижению) предложения в случае, когда спрос больше (меньше) предложения.   Гипотеза 2. Цена предлагаемого товара устанавливается товаропроизводителем на уровне, определяемом в соответствии с функцией предложения. Здесь товаропроизводитель действует формально: он знает, что кривая предложения в некотором смысле оптимальна. Поэтому он полагает, что при определении уровня цен с помощью функции предложения предлагаемый объем товара будет оптимальным. Гипотеза 3. Объем потребления товара не может превосходить ни объема предложения, ни объема спроса. Эта гипотеза означает, что если предложение меньше спроса, то потребление равно предложению. Если же спрос меньше предложения (т.е. имеет место избыточное предложение товара), то потребление равно спросу, а непроданный товар приводит к затовариванию. Таким образом, в данной модели связь между потреблением Сt, спросом Dt и предложением St в каждый период времени t можно представить в виде Ct = min(St , Dt ) . В модели В, в отличие от модели А, динамическая спираль наматывается уже против часовой стрелки. Таким образом, изменение гипотез о поведении потребителя и товаропроизводителя привело к изменению направления движения по спирали на противоположное. Поэтому в модели В при линейных функциях спроса и предложения колебания цен затухают и на рынке достигается равновесие. Изменение гипотез модели А привело не только к смене направления наматывания спирали, но, следовательно, и к изменению условия сходимости итерационного процесса на противоположное. Таким образом, если итерационный процесс динамики цен в одной из рассмотренных моделей (А или В) сходится, то в другой – расходится. Возникшее противоречие не является неразрешимым: сходимость последовательности цен к равновесному значению может быть получена за счет изменения гипотезы о принятии решения об объеме предложения (паутинообразная модель с обучением), в которой товаропроизводитель учитывает характер динамики цен и более точно прогнозирует условия на рынке. Рассмотрим модификацию модели В (модель ВМ), в которой текущее предложение определяется уравнением Данное соотношение означает, что товаропроизводитель при установлении цен и объемов предложения теперь уже ориентируется не на спрос предшествующего периода, а на некоторое среднее значение между спросом и предложением в этот период. Тем самым он учитывает в своих ожиданиях колебания цен, которые обучают его делать более адекватный прогноз предложения. При этом модель В является частным случаем данной динамической модели при r = 0. Это означает, что независимо от соотношения угловых коэффициентов функций спроса и предложения можно всегда подобрать такое значение параметра осреднения r, удовлетворяющее условию при котором итерационный процесс будет сходиться. Рассмотрим теперь модификацию модели А, которая приводит к уравнению с двойным распределенным запаздыванием. В модифицированной модели AM, в отличие от рассмотренной выше модели А, изменена первая гипотеза, которая теперь звучит так. Гипотеза 1m. Товаропроизводитель, принимая решение об объеме предложения, ориентируется на некоторое среднее значение цены за последние два предшествующих периода. Это означает, что товаропроизводитель при прогнозировании цен на рынке и определении соответствующих объемов предложения теперь уже ориентируется не на последнюю по времени цену, а принимает во внимание ее динамику. Колебания цен обучают его делать более адекватный прогноз реального уровня цен на завтра, исходя из информации о ценах сегодня и вчера. Введение в классическую паутинообразную модель (модель А) элементов обучения (т.е. более точного прогнозирования товаропроизводителем предполагаемой цены) улучшает сходимость динамического процесса и повышает устойчивость модели. При определенных значениях параметра осреднения r в паутинообразной модели с обучением (в модели AM) цены стремятся к равновесному значению даже при таких линейных функциях спроса и предложения, при которых колебания цены в классической паутинообразной модели неограниченно возрастают. Это означает, что обучение товаропроизводителя, правильное предвидение им цены (прогнозирование) носит принципиальный характер. Оказывается, что устойчивость равновесного решения определяется в конечном итоге не геометрическими свойствами кривых спроса и предложения (в случае линейных функций – отношением угловых коэффициентов), как это было в модели А, а реакцией экономических агентов на изменение рыночной конъюнктуры (в модели AM – реакцией товаропроизводителей на колебания цен). В случае паутинообразной модели с запаздыванием спроса соответствующая последовательность цен расходится, если последовательность цен в модели с запаздыванием предложения сходится, и наоборот. К этим же выводам приводит и классическая модель адаптации цены вальрасовского типа которая отражает рост (снижение) цен при избыточном спросе (предложении). Здесь r – положительный параметр, определяющий реакцию рынка (экономических участников) на дисбаланс спроса и предложения. В простейшей непрерывной модели рынка одного товара цена растет, если спрос превышает предложение, и падает, если предложение выше спроса [11, 20 и др.]. Сказанное может быть формализовано так: где k – коэффициент реакции цены на дисбаланс спроса и предложения. Пусть функции спроса и предложения линейные, и их уравнения имеют следующий вид: где Ре – значение равновесной цены; Р = P(t) – значение цены в момент времени t ; d и s – заданные положительные числа, определяющие наклон линий спроса и предложения соответственно. Будем считать, что в начальный момент времени t = 0 цена равнялась P(0) = Р0. Динамика цены задается уравнением Из него следует, что P(t) → Ре при t → ∞, т.е. со временем устанавливается равновесная цена. Все рассмотренные выше модели описывают взаимодействие различных экономических участников и предполагают наличие конкуренции. При совершенной конкуренции, когда на рынке действует много продавцов и много покупателей, ни один из них не в состоянии изменить цену. Однако опыт подсказывает, что при увеличении на рынке количества товаров его цена снижается. Это свидетельствует о том, что совершенная конкуренция – понятие достаточно абстрактное. Тем не менее, эта абстракция позволила теоретически обосновать такие важные экономические закономерности, как, например, функция предложения товара и кривая Лаффера. На конкурентном рынке цена растет при превышении спроса над предложением, а при избыточном предложении – падает, то это, в конечном итоге, приводит (при определенных условиях) к достижению рыночного равновесия. Это равновесие устойчиво в том смысле, что при заданной фиксированной структуре цен на рынок поставляется товар в количестве, равном спросу потребителя на этот товар. Исследование паутинообразных моделей позволило показать, что установление равновесия – достаточно сложный процесс, важную роль в котором играют ожидания экономических участников. Было установлено, в частности, что механизмы рыночного саморегулирования, действуя в направлении устойчивого равновесного состояния, далеко не всегда приводят к достижению равновесия на рынке. При, казалось бы, логически правильной реакции экономических агентов на изменение рыночной ситуации рыночные механизмы могут и не приводить к равновесию. Общим выводом из анализа рассмотренных динамических моделей рынка товаров является следующий: равновесие на конкурентном рынке достигается при условии адекватной реакции участников (потребителей и продавцов-товаропроизводителей) на изменение рыночной конъюнктуры. Рассмотрим теперь влияние монополизации на объемы предложения и рыночные цены, используя для этого модели монополии и дуополии, действующие на рынке одного товара. Монополия (монопольный рынок) представляет собой рыночную ситуацию, при которой предложение товаров сосредоточено в руках одного продавца (товаропроизводителя). Это может быть, например, в случае, когда одна фирма является единственным производителем и продавцом продукта, у которого нет близких заменителей. Доступ на рынок других фирм, производящих этот или функционально близкий ему товар, закрыт, конкуренция отсутствует. При этом на рынке действует много покупателей, а их общий спрос на товар падает при увеличении цены товара. В условиях монопольного рынка товаропроизводитель получает возможность повышать цену без улучшения качества продукции, регулировать объемы производства и т.д., стремясь максимизировать свою прибыль на основе использования известной ему информации о поведении потребителя, т.е. о кривой спроса. Это происходит следующим образом. Пусть, например, кривая спроса задается линейной функцией где а и d – положительные постоянные. Тогда для дохода R (выручки от продажи) получаем Поэтому в случае чистой монополии при линейной функции спроса кривая дохода представляет собой параболу, ветви которой направлены вниз (линия 1 на рис. 5). Для определения объема производства и цены в общем случае чистой монополии предположим, что функция издержек монополии задана уравнением С = C(Q). График функции издержек отмечен на рис. 5 цифрой 2. то в силу необходимого условия экстремума получаем R(Q) = C(Q) График функции прибыли I = I(Q) отмечен на рис. 5 цифрой 3. Решение уравнения задает оптимальный объем предложения Q0 и, как следствие, значение цены Р0 = P(Q0), которые устанавливает монополист. Геометрический смысл уравнения заключается в следующем: при Q = Q0 (т.е. в точке максимума прибыли) касательные к графикам функций дохода Y = R(Q) и издержек Y = C(Q) параллельны (рис. 5). Y 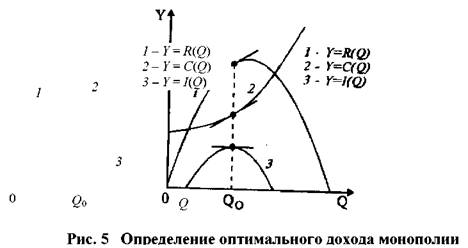 Другая геометрическая интерпретация связана с понятиями предельного дохода и предельных из-держек, поскольку равенство означает, что в точке максимума прибыли они равны: MR(Q0) = MC(Q0). Действительно, предельный доход MR, по определению, равен производной функции полного до-хода: MR(Q) = R(Q). Эта величина показывает, на сколько увеличивается доход при увеличении объема продаж на единицу. Итак, в случае монополии из условия MR(Q) = MC(Q) находим оптимальное (для монополиста) значение объема производства, после чего определяем значение цены товара. Одним из распространенных типов рыночной структуры, характерных для большинства развитых стран, является олигополия. На олигопольном рынке несколько фирм конкурируют друг с другом, и вступление на этот рынок других фирм затруднено. Рассмотрим простейший частный случай олигополии – дуополию, динамическая модель которой также подтверждает сделанные выше выводы об ограниченности стихийной рыночной самоорганизации. По определению, дуополия – рынок товара, который поставляют два продавца. Французский математик О. Курно, заложивший основы теории дуополии, трактовал принцип конкуренции следующим образом: покупатели объявляют цены товаров, а поставщики товаров приспосабливают объем выпуска к этим ценам. Каждый дуополист в модели О. Курно на основе информации о динамике спроса устанавливает объем выпуска продукции, предназначенный на продажу, в предположении, что объем предложения со стороны конкурента остается неизменным. И хотя каждый из продавцов в каждом периоде времени стремится максимизировать свою выгоду, динамика процесса конкуренции двух продавцов приводит к равновесному решению, более выгодному для покупателя, чем решение в случае чистой монополии. В 80-х гг. XIX в. другой французский математик – Ж. Бертран – построил модель дуополии, в которой цены устанавливают продавцы, причем каждый продавец устанавливает свою цену, исходя из того, что цена конкурента, а не объем его выпуска, остается неизменной. В изданной в 1897 г. Теории монополии Ф. Эджуорт сделал следующий шаг в развитии теории дуополии: ввел неопределенность взаимной реакции, в результате чего математическая модель стала недетерминированной. Ниже рассматривается классическая детерминированная модель дуополии в современной трактовке, а также ее модификация, в которой конкуренты изменяют свои решения в направлении их улучшения, не всегда при этом максимизируя эффект, как это делается в классических вариантах модели. В этом случае механизм саморегулирования не всегда приводит к установлению равновесия. Будем считать, что спрос на товар на этом рынке определяется многочисленными, но незначительными (по размеру покупок) потребителями, и что этот спрос снижается при увеличении цены. В модели принято, что объем покупок можно найти при помощи соответствующей функции спроса, которая известна на каждой фирме. Рассмотрим вариант модели дуополии, в котором сделан учет издержек производства. Предположим, что цена товара Р линейно убывает при увеличении общего предложения, т.е. P = a – b(X + Y), где X и Y – объемы товара, предлагаемого на рынке первой и второй монополиями; а и b – положительные постоянные. Предположим, что функция издержек каждой монополии линейна: С1 = k1Х; C2 = k2Y, где k1 и k2 – удельные затраты монополий при производстве единицы продукции. Cтратегия Курно заключается в том, что каждый дуополист поочередно максимизирует свою прибыль на основе известной ему информации об объемах поставок товара конкурентом. Однако всегда ли предприятие способно поставить на рынок товар в количестве, при котором достигается максимум его прибыли? Более реалистичным представляется поведение дуополистов, при котором они на каждом шаге стремятся не максимизировать, а просто увеличивать свою прибыль. В этом случае можно, например, использовать следующую модель динамики поставок товаров: 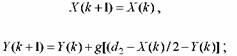 при k = 2n , n =1, 2, ... 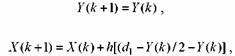 где g и h – положительные постоянные. Этот итерационный процесс в частном случае g – h = 1 совпадает со стратегией Курно, которая описывается системой 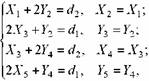 Если же эти постоянные g и h отличны от единицы, то итерационный процесс означает рост объема предложения со стороны каждой фирмы, если первая производная функции прибыли этой фирмы положительна, и наоборот, снижение объема предложения фирмы, если первая производная функции при-были этой фирмы отрицательна. Расчеты модели свидетельствуют о том, что характер динамики переменных в этом варианте модели дуополии зависит от значений параметров реакции дуополистов на отклонение поставок от оптимальных (g и h). При этом возможны не только сходимость к точке Курно, но и образование циклов, а также и расходимость итерационного процесса. В модели дуополии – рынка одного товара, обслуживаемого двумя продавцами (товаропроизводителями) – возможно использование различных стратегий. Если, например, дуополисты объединяются и образуют по сути единую монополию (картель), то это приводит к равновесию, при котором цены велики, а совокупный объем предложения мал. При этом общая прибыль бывших конкурентов достигает наибольшего значения. Развитие монополистической конкуренции, при которой каждое предприятие последовательно осуществляет свой выбор, стремясь достичь максимума собственной прибыли на каждом этапе (стратегия Курно), приводит уже к некооперативному равновесию. При этом происходит снижение рыночных цен, рост предложения и падение суммарной прибыли. В случае дальнейшего усиления конкуренции между товаропроизводителями (стратегия Стакельберга) цены и суммарная прибыль снова падают, а объем предложения на рынке еще более возрастает. В этой ситуации, наиболее выгодной для потребителя из всех рассмотренных, искушенный дуополист оказывается в более выигрышном положении (за счет своего конкурента), чем при использовании им стратегии Курно. Модель дуополии – хорошая иллюстрация тезиса о необходимости государственного регулирования монопольных рынков и введения антимонопольных, антитрестовских законов. Стремление увеличивать прибыль на каждом шаге (модифицированная стратегия Курно) может и не приводить к установлению равновесия на рынке. Оказывается также, что возможность достижения равновесия в модели монополистической конкуренции зависит от реакции дуополистов на отклонение объемов поставок от их оптимальных значений. ОГЛАВЛЕНИЕ ДИССЕРТАЦИИкандидат экономических наук Григорьев, Вячеслав Васильевич Введение |
