логистика. ВКР Логистика. Маршрутизация транспортных средств для доставки продукции группы компаний Транском
 Скачать 309.68 Kb. Скачать 309.68 Kb.
|
|
Глава III. Решение управленческих проблем компании в рамках вопроса маршрутизации транспортных средств. 3.1 Итоговое исследование: поиск кратчайшего пути между офисами компании В статье Смирнова А. А. «Оптимизация доставки готовой продукции и математический аппарат для ее достижения» приведены основные изменения, которые происходят после внедрения системы маршрутизации перевозок в любой компании. Маршрутизация перевозок позволяет уменьшать время выполнения каждого маршрута, снижать транспортные затраты на топливо, минимизировать количество опозданий к выгрузке у клиента и так далее. Автор работы приводит классификацию различных видов маршрутизации, которые зависят от конкретной системы доставки принятой в определенной компании. В классификацию входят: маршрутизация с ограничением по грузоподъемности, маршрутизация с ограничением по времени, маршрутизация с несколькими депо, маршрутизация с доставкой и возвратом товаров, маршрутизация с возвратом товаров и другие. В конце работы Смирнова А. А. приведена другая классификация наиболее часто используемых методов решения задач маршрутизации, которая сформирована исходя из первой классификации видов маршрутизации. В нее вошли следующие основные группы: простейшие методы, точные подходы, эвристические методы и мета-эвристики. Данные группы отличаются точностью решения и скоростью получения решения. Например, полный лексический перебор, входящий в группу простейших методов, является наиболее долгим методом, т.к. необходимо вручную перебрать все допустимые решения, которых может оказаться довольно большое количество. Также мета-эвристические методы дают более точный результат, чем обычные эвристические методы. В статье Зубарева А. К. «Планирование маршрутизации движения транспорта в условиях крупного города» рассматриваются различные методы решения проблем маршрутизации автотранспорта в пределах крупного города. Основная проблема маршрутизации, которую затрагивает автор в данной работе, связана с увеличивающимся количеством транспортных единиц на городских улицах. Транспортная инфраструктура крупных городов не позволяет быстро и с минимальными издержками перемещаться по оптимальному маршруту, т.к. развитие инфраструктуры происходит медленнее, чем увеличение транспорта на дорогах. В таких условиях задача маршрутизации может быть решена с помощью построения кольцевого маршрута. Для его построения могут использоваться линейное программирование и эвристические методы. Основное различие данных методов заключается в том, что линейное программирование дает более точное решение, чем эвристические методы. В основной части работы Зубарев А. К. производит сравнительный анализ шести методов, которые позволяют найти кратчайший путь движения грузовика при условии, что грузовик посетит все точки один раз. В анализ включены следующие методы поиска решений: метод 2-опт, алгоритм имитации отжига, приемлемость предельного значения, алгоритм всемирного потопа, алгоритм разрушения-восстановления и нейронные сети. После проведенного анализа наилучший результат показал алгоритм всемирного потопа, который показал наименьшую длину маршрута во всем диапазоне изменения количества точек. Однако данный метод является эвристическим, поэтому результат может быть занижен относительно других методов. С другой стороны, расчет минимальной протяженности пути занимает меньше времени у эвристического метода по сравнению с точными методами. Профессор технической инженерии университета Арканзаса Хэмди А. Таха в своей работе под названием «Введение в исследование операций» рассматривает основные разделы теории исследования операций: теория принятия решений, математическое программирование (детерминированное и стохастическое, линейное и нелинейное), теория управления запасами, теория игр, имитационное моделирование и теория массового обслуживания. Помимо теории в работе представлены различные типы задач, которые решены с помощью представленных математических моделей. Также большое внимание в работе уделяется специальному классу задач, которые относятся к сетевым моделям целочисленного программирования, а именно: транспортная, распределительная задачи и задача о назначениях. Наиболее общей моделью является распределительная задача. В работе выделена целая глава под сетевые модели, но они не могут быть применимы в рамках поставленной управленческой проблемы, т.к. основная цель модели – определение объемов перевозок из пунктов предложения в пункты спроса с минимальной стоимостью транспортировки. Более того, в сетевой модели нет последовательного посещения точек спроса. В то время как управленческая проблема компании Транском представляет собой классическую задачу маршрутизации перевозок. Данная задача заключается в том, чтобы найти самый выгодный маршрут, удовлетворяющий всем необходимым ограничениям, который проходит последовательно через все точки спроса с последующим возвратом на исходное место. В работе Хэмди А. Таха присутствует раздел целочисленного линейного программирования с разбором решений задачи коммивояжера. В данном разделе изучается применение двух методов к решению задачи коммивояжера: метод ветвей и границ и метод отсекающих плоскостей. Как уже говорилось ранее методы решения задачи коммивояжера могут быть применены только в совокупности с двухфазным алгоритмом решения задачи маршрутизации перевозок, который вводит различные ограничения на транспортировки. В работе Зайцева М.Г. и Варюхина С.Е. «Методы оптимизации управления и принятия решений» рассматриваются основные методы и модели для оптимизации управления и принятия решений. Работа представляет собой набор теоретической информации по различным тематикам исследования операций, а также приемы для решения практических задач. В рамках данного исследования предлагается распределение городов по методу Кларка-Райта в следующем порядке (графическое распределение):
Таблица 1. Распределение городов в рамках расчета по методу Кларка-Райта. Распределенные города не просто представляют собой условные точки, которые обозначены на условном графике. Каждая из этих точек предлагает свой собственный вариант выстраивания кратчайшего пути. Ключевыми точками являются Киев, Минск и Москва. Это точки отправления в условиях нашей задачи. В рамках поиска кратчайшего пути компанию представим все точки на графике, которые были описаны выше. Данное распределение наглядно покажет нам графическое распределение городов: 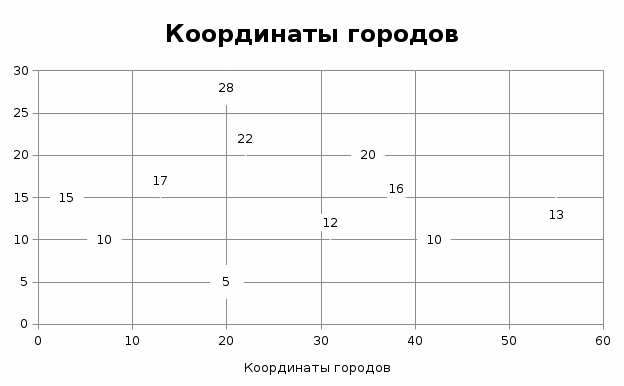 Рис. 2. Распределение городов на графике Также на графике обозначим требуемые от нас точки отправления. 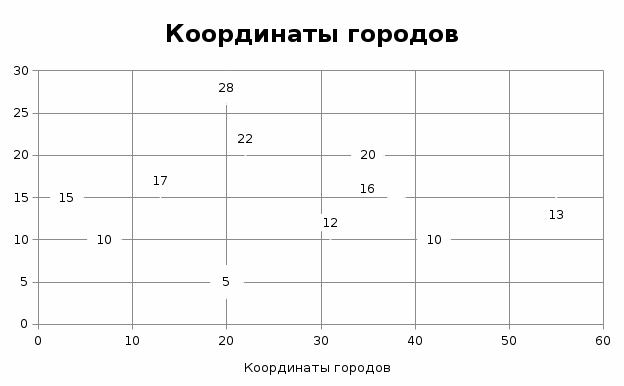 Рис 3. Возможные точки отправления в рамках нашей задачи: Москва, Киев, Минск. Таким образом, начальное распределение нам известно. По факту у нас есть несколько вариантов маршрутов: с начальной точкой в Киеве, Москве или Минске. В рамках предложенных логистических схем стоит выделить все условные маршруты между городами. Они представлены в таблице ниже.
Таблица 2. Все расстояния между городами и расчет кратчайшего пути. Таким образом, мы, задав определенную формулу распределения точек получилось определить длину кратчайшего пути, которая равна 58,5018 в рамках нашего распределения. При этом стоит выделить условные распределения разрешенных маршрутов в рамках нашего расчета в эксель:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
