логистика. ВКР Логистика. Маршрутизация транспортных средств для доставки продукции группы компаний Транском

• Название: Маршрутизация транспортных средств для доставки продукции группы компаний Транском
• Анкор: логистика
• Дата: 13.09.2022
• Размер: 309.68 Kb.
• Имя файла: ВКР Логистика.docx
• Тип: Реферат; #674221
• страница: 2 из 4

Глава II. Анализ задач маршрутизации транспортных средств

2.1 Структура задач маршрутизации транспортных средств

В рамках данного параграфа мы изучим обозначения и структуру задач по маршрутизации. Для полноценного понимания метода во всей главе будут рассмотрены работы, которые предлагают нашему вниманию разный уровень решения управленческой проблемы.

В одной отдельно взятой, условной компании запросы на транспортировку состоят из распределения товаров с одного склада, обозначенного как точка 0, в заданный набор из n других точек, обычно называемых клиентами, N = {1, 2,..., n}.

Сумма, которая должна быть доставлена клиенту i ∈ N, представляет собой спрос клиента, который задается скаляром qi ≥ 0, например, весом товара, подлежащего доставке. Предполагается, что автопарк K = {1, 2,...,|K|} является однородным, что означает, что |K| транспортных средств имеется в наличии на складе, все они имеют одинаковую вместимость Q > 0 и работают с одинаковыми затратами.

Транспортное средство, которое обслуживает подмножество клиентов S ⊆ N, начинается со склада, перемещается один раз к каждому из клиентов в S и, наконец, возвращается на склад. Транспортное средство, перемещающееся из i в j, несет транспортные расходы ci j . Данная информация может быть структурирована с использованием неориентированного или ориентированного графа.

Пусть V = {0} ∪ N = {0, 1,..., n} - множество вершин (или узлов). Удобно определить q0 := 0 для депо. В симметричном случае, т.е. когда стоимость перемещения между i и j не зависит от направления, т.е. либо от i к j, либо от j к i, базовый граф G = (V, E) является полным и неориентированным с набором ребер E = {e = {i, j } = { j ,i} : i, j ∈ V,i 6= j } и затраты на ребро ci j для {i, j } ∈ E.

В противном случае, если хотя бы одна пара вершин i, j ∈ V имеет асимметричные затраты ci j 6= cj i, то лежащее в основе граф представляет собой полный орграф G = (V,A) с набором дуг A = {(i, j) ∈ V ×V : i6= j } и стоимостью дуги ci j для (i, j) ∈ A.

Стоит обратить внимание, что |E| = n(n + 1) /2 и |A| = n (n + 1), так что оба условных графика содержат O (n 2 ) ссылок. В целом, условная компания, о которой мы говорим однозначно определяется полным взвешенным графиком G = (V, E, ci j , qi) или орграфом G = (V,A, ci j , qi ) вместе с размером |K| парка транспортных средств K и вместимостью транспортного средства Q. Маршрут (или маршрут) представляет собой последовательность r = (i 0 ,i 1,i 2,...,i s ,i s+1 ) с i 0 = i s+1 = 0, в которой множество S = {i 1,...,i s } ⊆ N клиентов посещается. Маршрут r имеет стоимость c(r) = Ps p=0 ci p ,i p+1 . Это возможно, если ограничение пропускной способности q(S) := P i∈S qi ≤ Q выполняется, и ни один клиент не посещается более одного раза, т.е. i j 6= i k для всех 1 ≤ j < k ≤ s. В этом случае говорят, что S ⊆ N является допустимым кластером. Решение для CVRP состоит из |K| возможных маршрутов, по одному для каждого транспортного средства k ∈ K.

Маршруты r1, r2,..., r|K| и соответствующие кластеры S1, S2,..., S|K| обеспечивают возможное решение CVRP, если все маршруты выполнимы, а кластеры образуют раздел N. В заключение, CVRP состоит из двух взаимозависимых задач:

- разделение набора N клиентов на возможные кластеры S1 ,..., S|K|;

- маршрут каждого транспортного средства k ∈ K через {0} ∪ Sk.

Последняя задача требует решения задачи коммивояжера (TSP) над {0} ∪ Sk. Обе задачи взаимосвязаны, поскольку стоимость кластера зависит от маршрутизации, а маршрутизация требует кластеров в качестве входных данных.³

В целом, именно так выглядит построение математической модели для решения задач, связанных с маршрутизацией и поиском наименьшего пути. Очевидно, что задачу можно создавать не под однородный товар внутри грузвового транспорта. Так, аналогом доставки клиентам в этом случае является сборный груз от клиентов (LTL) от клиентов.

Различные варианты VRP-задач возникают, когда сбор и распределение (или самовывоз и доставка) материала происходят одновременно по маршруту. При этом по-прежнему предполагается, что распределение начинается, а сбор заканчивается на складе.

Поэтому проблемы со сбором также известны как VRP «многие к одному», а проблемы с распределением - как VRP «один ко многим». Первый и, вероятно, самый простой вариант - это VRP с обратными путями.

Например, при транспортировке крупногабаритных материалов все поставки так называемым клиентам должны выполняться в первую очередь так, чтобы транспортное средство было пустым, когда оно прибудет в первый пункт сбора. Поскольку любое перемещение от клиента обратного пути к клиенту прямого пути запрещено, модель VRP1 остается применимой, если соответствующие дуги удалены из набора дуг A (в качестве альтернативы можно установить стоимость этих дуг на достаточно большое число M).

Ограничения при обратной транспортировке возникают из-за сложности перестановки загруженных предметов внутри транспортного средства. Если загрузочное пространство допускает перестановки, например, потому, что транспортное средство может быть загружено сзади и спереди или со всех сторон, в результате возникает проблема VRP со смешанными поставками и сборами или просто смешанный VRPB.⁴ Здесь пропускная способность транспортного средства должна проверяться для каждого пройденного края (или дуги); т.е. нагрузка, уже собранная от клиентов обратной перевозки, плюс нагрузка, которая должна быть доставлена клиентам, никогда не может превышать заданную пропускную способность.

В то время как каждому клиенту в VRPB и MVRPB требуется либо доставка, либо сбор, но не и то, и другое, VRP с одновременным получением и доставкой включает в себя два запроса на перевозку для каждого клиента, а именно доставку со склада клиенту, и самовывоз от клиента к депо.⁵

Оба запроса на перевозку должны быть выполнены одним транспортным средством за один визит. Такая ситуация часто встречается в нескольких реальных приложениях, таких как доставка напитков и одновременный сбор пустых бутылок, а также перевозка на автобусе вновь прибывающих и покидающих отель гостей между местным аэропортом и несколькими отелями (это обычная практика туроператоров во многих курортных регионах). Опять же, ограничение вместимости гарантирует, что ни одно транспортное средство не будет перегружено в любой точке. Интересно, что существует простой критерий для проверки того, может ли данный набор клиентов S ⊆ N быть реально обслужен одним транспортным средством: существует приемлемый маршрут, если ни общая сумма, подлежащая доставке, ни сумма, подлежащая сбору, не превышают вместимость транспортного средства. Нужно просто построить маршрут таким образом, чтобы клиенты с большей суммой, подлежащей доставке, чем подлежащей сбору, посещались первыми на маршруте. Разновидностью VRPSDP является VRP с разделяемыми поставками и приемами (VRPDDP). Здесь доставка и самовывоз у клиента могут быть выполнены за один визит или за два отдельных визита одним и тем же транспортным средством. Поскольку требуется меньшая пропускная способность, когда доставка должным образом предшествует самовывозу, в VRPDDP возможна экономия затрат по сравнению с VRPSDP. Форма маршрутов является более общей и включает в себя так называемые маршруты лассо и другие.⁶

Проблемы с самовывозом и доставкой - это VRP, в которых запросы на транспортировку состоят из двухточечных перевозок. Точнее, каждый запрос на перевозку состоит из перемещения товаров или людей между двумя конкретными местами, одним, где кого-то или что-то забирают, и соответствующим местом для доставки. Эта проблема называется проблемой получения и доставки в контексте транспортировки грузов.⁷ Приложения включают в себя грузовые перевозки, подобные тем, которые описаны М. Савельсбергом и М. Солом.⁸ В контексте пассажирских перевозок эта проблема известна как проблема набора номера. Существуют приложения для маршрутизации автобусов для учащихся, пациентов, инвалидов и пожилых людей. Почти все варианты DARP включают ограничения по временному окну. Часто уровни обслуживания и удобство пользователя учитываются либо с помощью ограничений, либо в целевой функции. В нашем же случае, актуальным будет только доставка груза с пункта А в множество пунктов B, или же в один пункт C.


2.2 Обзор задач по поиску кратчайшего пути

Выбор кратчайшего маршрута для движения мобильных объектов определяет их эффективность и экономическую эффективность. Такие задачи для отдельных транспортных средств решаются методами изучения операций над графами, в частности, на основе известных алгоритмов Дейкстры, подробно рассмотренных у исследователей Черткова А., Беллмана-Форда Р., Сахаров В.

Многие научные работы в области транспортных систем, логистики и исследований операций посвящены решению проблем повышения эффективности международных перевозок грузов. К основным характеристикам дорожных сетей относятся: максимальный поток в сети и кратчайшие расстояния в сети.

Для решения задачи оптимизации транспортной сети необходимо уметь сводить сетевое представление транспортной задачи к матричному виду, для которого существует практический математический аппарат оптимизации перевозок.

Существующие методы решения задачи максимального потока в транспортной сети удобно использовать только для плоской сети. Алгоритм «максимального потока» позволяет оптимизировать решение задачи, но не учитывает особенности транспортных сетей. Необходимо расширить метод для решения проблемы оптимизации транспортных сетей с ограничениями пропускной способности сети и без них.

В процессе функционирования различных компонентов транспортных систем возникает постоянная необходимость решения проблем, связанных с их работой в качестве систем массового обслуживания различных типов требований. Это связано с тем, что их назначением, как правило, является обслуживание различных потребителей транспортных услуг (заказов). Поэтому решение задач анализа и оптимизации режимов работы различных звеньев транспортных систем является достаточно актуальным и способно значительно повысить эффективность использования транспорта в различных отраслях экономики.

Функционирование отдельных компонентов транспортных систем (TS) рассматривается в этом случае как набор последовательно связанных входящих потоков требований к обслуживанию (транспортные средства, пассажиры и т.д.), каналов обслуживания (контрольно-пропускные пункты, станции технического обслуживания и т.д.) и исходящих потоков требований после обслуживания.

Разнообразие применений теории массового обслуживания определяет растущий интерес к ней, а сложность возникающих проблем не позволяет получать комплексные решения, основанные на аналитических методах, даже при численной реализации последних. В таких ситуациях обязательно использовать имитационное моделирование, которое является незаменимым инструментом для анализа эксплуатационных и многих других характеристик и параметров исследуемых систем. Перспективным направлением исследований является использование современных компьютерных информационных технологий в имитационном моделировании применительно к системам массового обслуживания транспорта.

Реализации процесса работы системы массового обслуживания (QSO) моделируются на компьютере с использованием ряда случайных или псевдослучайных величин. Усреднение результатов моделирования по времени работы модели или по количеству реализаций процесса позволяет методами математической статистики получать желаемые характеристики системы. Имитационная модель QSO - это модель, которая показывает, как ведет себя система и как ее состояние будет меняться с течением времени при заданном потоке требований, поступающих на входные данные системы. Параметры входного потока требований являются внешними параметрами QSO.

Исходными параметрами являются значения, характеризующие свойства системы и качество ее функционирования. Имитационное моделирование позволяет исследовать СМК с различными типами входных потоков и разной интенсивностью системных требований, а также различной дисциплиной требований к обслуживанию.

Сегодня в мире программного обеспечения GPSSW (General Purpose Simulation System World) является самой мощной и универсальной средой моделирования для профессионального моделирования широкого спектра процессов и систем.

Эта система предназначена для моделирования дискретных, в основном СМК, и непрерывных систем. Это очень эффективный инструмент моделирования, независимый от ограничений аналитических и численных методов, достаточно «прозрачный», который позволяет выполнять нестандартную обработку данных и устраняет многие нетривиальные проблемы программирования и отладки моделей.

Область решений таких оптимизационных задач очень широка, а именно от выбора маршрутов движения зависит грузопоток и скорость доставки, как итог – зависит в принципе поставка нужного сырья, например, на производство

Алгоритм Дейкстры.

Алгоритм Дейкстры предназначен для решения задачи поиска кратчайшего пути на графе. Для заданного ориентированного взвешенного графа с неотрицательными весами алгоритм находит кратчайшие расстояния от выделенной вершины - источника до всех остальных вершин графа.

Алгоритм Дейкстры является асимптотически быстрейшим из известных последовательных алгоритмов для данного класса задач.

Математическое обоснование Алгоритма Дейкстры.

Пусть задан граф G=(V,E) с весами ребер f(e) и выделенной вершинойисточником u.

Обозначим через d(v) кратчайшее расстояние от источника u до

вершины v.

Пусть уже вычислены все расстояния, не превосходящие некоторого

числа r, то есть расстояния до вершин из множества Vr={v∈V∣d(v)≤r}.

Пусть(v,w)∈argmin{d(v)+f(e)∣v∈V,e=(v,w)∈E}.

Тогда d(w)=d(v)+f(e)d(w), и v лежит на кратчайшем пути от u к w.

Величины

d+(w)=d(v)+f(e), (11)

где:

v∈Vr , e=(v,w)∈E называются предполагаемыми расстояниями и

являются оценкой сверху для настоящих расстояний: d(w)≤d+(w).

Алгоритм Дейкстры на каждом шаге находит вершину с наименьшим предполагаемым расстоянием, помечает её как посещённую и обновляет предполагаемые расстояния для всех концов рёбер, исходящих из неё. Входные данные: взвешенный граф (V, E, W) (n вершин vi и m ребер ej=(vj(1),vj(2)) с весами fj), вершина-источник u.

Объём входных данных: O(m+n).

Выходные данные (возможные варианты):

- для каждой вершины v исходного графа – последнее ребро e∗v= (w,v),

лежащее на кратчайшем пути от вершины u к v, или соответствующая

вершина w; для каждой вершины v исходного графа – суммарный вес f∗(v)

кратчайшего пути от вершины u к v.

Объём выходных данных: O(n).

Макроструктура алгоритма Дейкстры имеет вид:

Q := новая приоритетная очередь

Для каждого v ∈ V:

Если v = u то d(v) := 0 else d(v) := ∞

Q.вставить(v, d(v))

Пока Q ≠ ∅:

v := Q.удалить_min()

Для каждого e = (v, w) ∈ E:

Если d(w) > d(v) + f(e):

d(w) := d(v) + f(e)

Q.уменьшить_ключ(w, d(w))

Алгоритм Дейкстры использует структуру данных для хранения и запроса частичных решений, отсортированных по расстоянию от начала. Исходный алгоритм использует очередь с минимальным приоритетом и выполняется за времяO(|V| 2 ). При использовании фибоначчиевой кучи время вычисления минимума сокращается до O(|E|+|V|log|V|), что является асимптотически наилучшим известным результатом для данного класса задач.⁹

Генетический алгоритм (GA).

Генетический алгоритм - это стохастический метод глобального поиска, который выглядит как естественный процесс эволюции с использованием генетических операторов. Доказано, что генетический алгоритм эффективен в самых разных областях поиска.

Генетический алгоритм - это метод оптимизации и поиска, основанный на принципах генетики и естественного отбора. GA начинается, как и любой другой алгоритм оптимизации, с определения переменных оптимизации, функции затрат и стоимости. Он заканчивается, как и другие алгоритмы оптимизации, проверкой на сходимость.

Генетический алгоритм (GA) - это метод оптимизации и поиска, основанный на принципах генетики и естественного отбора. ГА позволяет популяции, состоящей из множества хромосом, эволюционировать в соответствии с определенными правилами отбора до состояния, которое максимизирует «приспособленность» (или минимизирует функцию затрат).

Метод был разработан Джоном Холландом. Он был первым, кто попытался разработать теоретическую основу для газа с помощью своей теоремы о схеме. Работа Де Йонга показала полезность ГА для оптимизации функций и предприняла первые согласованные усилия по поиску оптимизированных параметров.

Генетические операции - это скрещивание и мутация. Оператор кроссовера создает новые хромосомы путем рекомбинации генетического материала двух хромосом, считающихся родительскими. Хромосомы с более высокой приспособленностью отбираются в качестве родителей и ‘передают’ свои гены следующему поколению.

Кроссоверы позволяют использовать успешные подпространства пространства решений. Оператор мутации случайным образом изменяет один или несколько генов в хромосоме. Мутации добавляют генетическое разнообразие популяции. Благодаря мутации GAs может искать ранее неисследованные участки пространства решений. Благодаря скрещиванию и мутациям GAs способны одновременно исследовать новые подпространства, используя успешные из них

Обзор проблемы кратчайшего пути.

Эта проблема имеет много полезных применений. Протоколы маршрутизации, используемые в большинстве современных компьютерных сетей, основаны на алгоритмах кратчайшего пути. Следовательно, это стало предметом обширных исследований. Дейкстра предоставил уже хорошо известный алгоритм. Флойд ослабил ограничение, согласно которому все веса должны быть неотрицательными. Иногда бывает полезно найти два, три или k кратчайших путей. Когда число узлов равно n, а число ребер равно m, Эппштейн дает алгоритм, который находит k кратчайших путей.

Генетические алгоритмы являются одним из самых мощных и успешных методов в методах стохастического поиска и оптимизации, основанных на принципах теории эволюции.

Таким образом мы приходим к выводу о том, что существует огромное количество вариаций в рамках решения задач по поиску кратчайшего маршрута. Предполагается, что каждый из этих подходов имеет свойственные только ему плюсы и минусы. Разница между алгоритмами заключается в том, что каждый из них является оптимальным для определенных ситуаций. Так, например, алгоритм Кларка-Райта выглядит наиболее понятным для исследователей, не погруженных в глубокое понимание математики. При этом, например, Алгоритм Р. Флойда и С. Уоршелла позволит нам найти в предложенной матрице дистанций между получателями кратчайшие пути между получателями продукции.

2.3 Выбор алгоритма решения транспортной задачи

Г. Кларком и Дж. Райтом в качестве показателя улучшения маршрутов предложена экономия пробега. Предположим, у нас есть два получателя i и j, которым требуется доставить товар. Можно доставить товар либо двумя радиальными маршрутами, либо одним кольцевым.

В первом случае общий пробег составит:

L1 = 2l0i + 2l0j

Во втором случае общий пробег составит:

L2 = l0i + lij + l0j

Экономия (функция выгоды) при применении кольцевого маршрута вместо двух радиальных составит: f (i, j) = L1 – L2 = l0i + l0j – lij

При решении задачи развозки мелкопартионных грузов мы имеем n получателей. Составляем систему из n радиальных маршрутов {0, i, 0}, где i = (1, 2, 3, 4, …, n).

Система радиальных маршрутов удовлетворяет условиям задачи развозки, но содержит много мелких маршрутов. Эту систему преобразовываем, постепенно объединяя маршруты (превращая радиальные маршруты в кольцевые). Маршруты объединяем с учетом значений функции выгоды, стремясь к наибольшему сокращению длины маршрутов.

Для того чтобы определить сам путь, т. е. последовательность промежуточных получателей, через которых будет проходить этот кратчайший путь, мы применим алгоритм Дейкстры. После того как мы отыщем кратчайшие расстояния между любой парой получателей и узнаем сами пути, остается задействовать алгоритм Кларка–Райта, который сформирует оптимальные маршруты.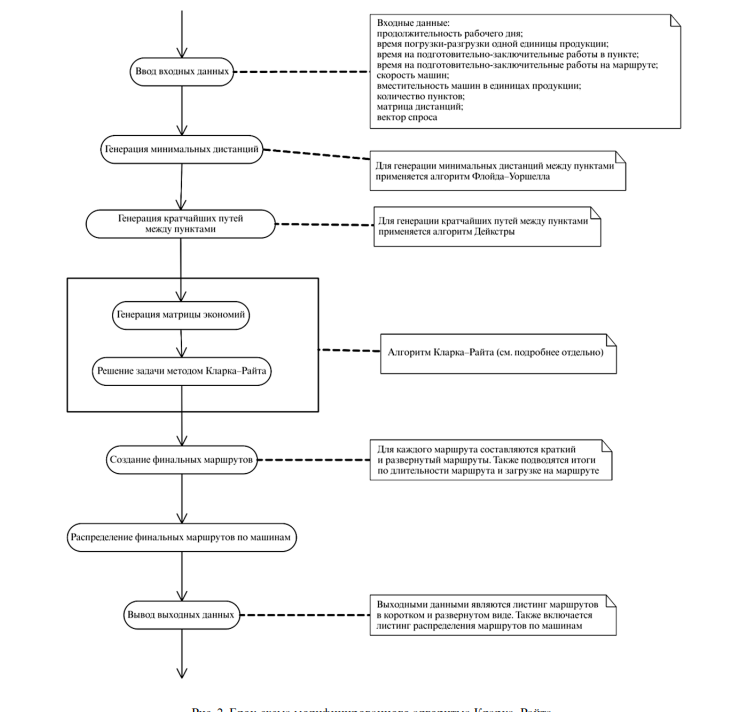


Рис 1. Блок-схема модифицированного алгоритма Кларка–Райта.

Исходя из представленной схемы метода алгоритма Кларка-Райта можно сделать вывод о том, что он подходит под управленческую задачу, которая была поставлена в первой главе работы. Таким образом, выбор алгоритма Кларка-Райта предполагает под собой оптимальный вариант. Предварительно мы имеем определенное количество офисов по Европе. Учитывая, что наша задача – найти кратчайший маршрут независимо от того какая политическая ситуация складывается в рамках санкций ЕС в отношении России. Реальность такова, что у компании есть офис на территориях с осложненной политической ситуацией, но в данной работе рассматривается вариант, при котором осуществление перевозок происходит в штатном режиме и не зависит от краткосрочных издержек. Итогом главы является тот факт, что при всем разнообразии методов был выбран один, который предполагает под собой определенные возможности для транспортной компании по транспортировки и перевалке грузов между своими складами в европейских столицах. В третьей главе будет производиться расчет кратчайшего пути, который может связать ряд центральных городов Европы в рамках выстраивания логистической схемы.