Математическая обработка. Курсовая работа Бельских АМ ГМО-18-1. Математическая обработка результатов эксперимента

• Название: Математическая обработка результатов эксперимента
• Анкор: Математическая обработка
• Дата: 26.01.2021
• Размер: 288.51 Kb.
• Имя файла: Курсовая работа Бельских АМ ГМО-18-1.docx
• Тип: Курсовая; #171394
• страница: 1 из 4

М ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВО "УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ГОРНЫЙ УНИВЕРСИТЕТ"

КАФЕДРА ГОРНОЙ МЕХАНИКИ

Курсовая работа

по задачам на тему

«Математическая обработка результатов эксперимента»

Преподаватель: Потапов В.Я.

Студент: Бельских А.М.

Группа: ГМО-18-1


Екатеринбург 2020 г.

Целью данных задач является определение с помощью критерия Пирсона вида закона распределения и определение минимального числа реализаций случайных величин, обеспечивающих с 90% надежностью совпадение результатов моделирования с теоретическим распределением.

Для моделирования равномерно и нормально распределенных величин необходимо знать выборочное среднее, а также максимальное и минимальное значение переменной.

С достаточной для инженерных расчетов точностью для нормального закона распределения среднее квадратичное отклонение и выборочное среднее можно определить из уравнений:





При моделировании экспоненциально распределенной случайной величины необходимо знать один параметр ­– выборочное среднее, которое равно среднему квадратичному отклонению.

Для моделирования случайной величины, распределенной по закону Вейбулла, необходимо знать три параметра: α, β, γ. Обычно при моделировании один из параметров принимается равным нулю, а вариацией двух других параметров обеспечивают необходимую форму кривой плотности вероятности.

Распределение Релея однопараметрическое (а≠0) и является частным случаем распределения Вейбулла.

Проверка соответствия полученного распределения теоретическому производится в следующем порядке:

1. Строится гистограмма распределения.

2. Определяется теоретическое число реализаций в каждом интервале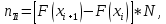



где N – суммарное число реализаций случайной величины

F(x) – значение интегральной функции в токе x.

3.Находим значение критерия Пирсона.



4. Определяется число степеней свободы

5. По таблице для заданного уровня надёжности находится табличное значение критерия Пирсона .

Если > 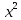– то смоделированная совокупность незначительно отличается от теоретической.

Таблица «Распределения Пирсона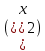

φ	0,99	0,98	0,95	0,90
1	0,00016	0,00063	0,00393	0,0158
2	0,0201	0,0404	0,103	0,211
3	0,115	0,185	0,352	0,584
4	0,297	0,429	0,711	1,064
5	0,554	0,752	1,145	1,61
6	0,872	1,134	1,635	2,204
7	1,239	1,564	2,167	2,833
8	1,646	2,032	2,733	3,49
9	2,088	2,532	3,325	4,168
10	2,588	3,059	3,94	4,865
11	3,053	3,609	4,575	5,578
12	3,571	4,178	5,226	6,304
13	4,107	4,765	5,892	7,042
14	4,660	5,368	6,571	7,790
15	5,229	5,985	7,261	8,547
16	5,812	6,614	7,962	9,312

Полужирным выделено теоретическое распределение вероятности для 90 % совпадения при K_инт=16.

Задача №1

Моделирование случайной равномерной распределение величины

(Задача решена на основании методики, представленной в [1, стр.5])

Исходные данные
1. Число случайных величин	N	1000
2. Минимальное значение случайной величины	Xmin	4
3. Максимальное значение случайной величины	Xmax	40
4. Параметр случайного распределения a	a	0
5. Параметр случайного распределения b	b	0
6. Параметр случайного распределения g	g	0
7. Число интервалов случайной величины	n	10

Результаты расчетов

№ интервала	Интервал		Число попаданий в интервал
1	1,00	4,90	110
2	4,90	8,80	95
3	8,80	12,70	100
4	12,70	16,60	114
5	16,60	20,50	95
6	20,50	24,40	91
7	24,40	28,30	106
8	28,30	32,20	84
9	32,20	36,10	95
10	36,10	40,00	110

По расчетным формулам вывели следующие значения:

ni	}{^2
100	1
100	0,25
100	0
100	1,96
100	0,25
100	0,81
100	0,36
100	2,56
100	0,25
100	1
}{^2 Сумма	8,44

Смоделированная совокупность (8,44) меньше теоритической (8,547) при 90% вероятности. Следовательно, задача решена верно. Среднее число расчетов для получения итогого результата – 16.

Задача №2

Моделирование случайной экспоненциально распределенной величины

Исходные данные

1. Число случайных величин	N	100000
2. Минимальное значение случайной величны	Xmin	0
3. Максимальное значение случайной величны	Xmax	40
4. Среднее значение случайной величины	Xср	4
7. Число интервалов случайной величины	n	10

Результаты расчетов

№ интервала	Интервал		Число попаданий в интервал
1	0,00	4,00	63336
2	4,00	8,00	23224
3	8,00	12,00	8508
4	12,00	16,00	3097
5	16,00	20,00	1157
6	20,00	24,00	418
7	24,00	28,00	168
8	28,00	32,00	61
9	32,00	36,00	23
10	36,00	40,00	2