Математическая обработка. Курсовая работа Бельских АМ ГМО-18-1. Математическая обработка результатов эксперимента

• Название: Математическая обработка результатов эксперимента
• Анкор: Математическая обработка
• Дата: 26.01.2021
• Размер: 288.51 Kb.
• Имя файла: Курсовая работа Бельских АМ ГМО-18-1.docx
• Тип: Курсовая; #171394
• страница: 3 из 4

Задача №5

Моделирование случайной величины,
распределенной по закону Рэлея

Исходные данные

1. Число случайных величин	N	1000
2. Минимальное значение случайной величины	Xmin	0
3. Максимальное значение случайной величины	Xmax	12
4. Параметр случайного распределения α	α	2,73
5. Параметр случайного распределения β	β	0
6. Параметр случайного распределения γ	γ	0
7. Число интервалов случайной величины	n	10

Результаты расчетов

№ интервала	Интервал		Число попаданий в интервал
1	0,00	1,20	69
2	1,20	2,40	227
3	2,40	3,60	296
4	3,60	4,80	212
5	4,80	6,00	120
6	6,00	7,20	50
7	7,20	8,40	16
8	8,40	9,60	6
9	9,60	10,80	2
10	10,80	12,00	1

По расчетным формулам вывели следующие значения:

F(x)	F(x+1)	ni		Распределение x^2
0	0,0648871	88		4,102273
0,0648871	0,2353614	234		0,209402
0,2353614	0,4532654	261		4,693487
0,4532654	0,6581584	205		0,239024
0,6581584	0,8131033	124		0,129032
0,8131033	0,9106476	59		1,372881
0,9106476	0,9626458	19		0,473684
0,9626458	0,9863447	7		0,142857
0,9863447	0,9956350	3		0,5
0,9956350	0,9987799	1		0
	х2 сумма

В результате расчетов установлено, что полученный вид функции соответствует распределению по закону Рэлея. Сравнение по критерию Пирсона подтвердило соответствие данному закону, в среднем при каждой десятой попытке.

Индивидуальная расчетная работа.

Расчет вероятности безотказной работы валов.

Исходные данные:

Jдв кг м2	J2 кг м2	Z1	Z2	ωдв, H, ряд/с	Тдв, Hм	Тср, Hм	в	Тmin Hм
33	43	19	37	150	300	240	780	0

J_i = J_дв(Z ₂ /Z ₁ ) ² = 33(37 /19)²= 125,14 = 125 кг м² .

1. Определяем диаметры ведущего (d₁) и ведомого (d₂) валов: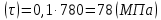

;



;





где Т_дв – номинальный движущий момент, развиваемый двигателем; Н м – пониженные допускаемые напряжения на кручение, МПа;

δв – предел прочности материала, МПа;

Т₂ – номинальный движущий момент на ведомом валу, равен постоянному сопротивлению, Н м.

Длина ведущего (L₁) и ведомого (L₂) валов:

L₁=4 d₁= 4 0,027=110 мм или 0,110 м;

L₂=4 d₂= 8 0,033= 133 мм или 0,133 м;

2. 
   Определяем собственные жесткости ведущего (С_1с) ведомого
   

(С_2с) валов:

;

где G – модуль сдвига равный 810¹⁰ Па;

;

2. 
   Определяем приведенные жесткости ведущего (С₁,) и ведомого валов (С₂):
   

С₁ = С_1с U²= 37925(1,95)² = 144 210 Н м;

С₂=С_2с= 69 996 Н м.

2. 
   Определяем эквивалентную суммарную жесткость упругого элемента (С):
   

С = (С₁ С_2c) / (С₁ + С_2c) = ( 144210 69996) / (144210+ 69996)= 47 123 Н м.

2. 
   Определяем частоту переменной нагрузки (ω_max; ω_min)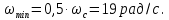
   

где ω_c – собственная частота динамических колебаний системы, рад/с.

2. 
   Определяем коэффициент деформирования (β):
   

ψ= 0,2;

Выборочное среднее переменной нагрузки принимается равной постоянному моменту сопротивления:

Т_с =Т_n= 240 Н м ;

Т_n =2 Т_с = 2 240 =480Н м;

Среднее отклонение:

δ _т.п= 2 Т_с /6 = 480 / 6 = 80.

2. 
   Определяем минимальный шаг интегрирования:
   

N = 100,

где N – частота циклов нагрузки, выбирается произвольно;

T_min – период изменений внешней нагрузки.

2. 
   Определяем выборочное среднее (τ)
   

Исходные данные:

Число циклов нагрузки	N	100
Минимальное значение частоты собственных колебаний, рад/с	ωmin	19
Максимальное значение частоты собственных колебаний, рад/с	­ωmax	57,4
Ведущая масса, кг/м2	m1	125
Ведомая масса, кг/м2	m2	43
Коэффициент жесткости, Н·м	C1	47123
Коэффициент деформирования, Н·с·м	b	39.1
Средняя нагрузка, Н·м	Tcp­	240
Максимальная нагрузка, Н·м	Tmax	480
Минимальная нагрузка, Н·м	Tmin	0.1095
Шаг интегрирования по времени, с	∆τ	0.001095
Максимальный движущийся момент, Н·м	Мдв	780
Номинальная скорость вращения двигателя, рад/с	ωН	150
Число зубьев ведущей шестерни	Z1	19
Число зубьев ведомой шестерни	Z2	37

Результат расчетов

№ интервала	Интервал		Число попаданий в интервал
1	-753,66	-447,97		84
2	-447,97	-142,28		362
3	-142,28	163,41		1994
4	163,41	469,10		2089
5	469,10	774,79		377
6	774,79	1080,48		94

Для каждого интервала необходимо найти выборочное среднее динамического момента в упругом звене. Проведем этот и следующие расчеты при помощи Excel:



Результат:

T1	-600,815
T2	-295,125
T3	10,565
T4	316,255
T5	621,945
T6	927,635
Tс	0,196092

Находим выборочное среднее для каждого интервала:

0,0235

Результат:

p1	0,0168
p2	0,0724
p3	0,3988
p4	0,4178
p5	0,0754
p6	0,0188

Находим дисперсию напряжения для каждого интервала и результирующую:

1	-10,094
2	-21,367
3	4,213
4	132,131
5	46,895
6	17,440
	169,218

Находится характеристика безопасности и по интегралу вероятности находится ВБР:



Результат:



Ддя безотказной работы требуется соблюдение условия р(t)>-0.95.

При полученном значении , р попадает в интервал 0,998-0,999, следовательно наша вероятпость примерно равна: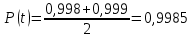



Рассчитанное значение удовлетворяет условиям, следовательно, весь расчет был произведён верно, и внесение изменений в конструктивные параметры валов не требуется.