Мм в истории. Математические методы в истории. Математические методы в истории
 Скачать 390.5 Kb.
|
. Выборочный методЗачастую историки имеют в своем распоряжении большой массив источников и данных, которые они не в состоянии полностью обработать. Это касается, в первую очередь, исследований по Новой и Новейшей истории. С другой стороны, чем глубже приходится заглядывать вглубь веков, тем меньшим количеством информации можно оперировать. В обоих этих случаях небесполезно использовать так называемый выборочный метод, суть которого заключается в замене сплошного обследования массовых однородных объектов частичным их исследованием. При этом из генеральной совокупности выделяется часть элементов, именуемая выборкой, и результаты обработки выборочных данных в итоге обобщаются на всю совокупность. Основой для характеристики всей совокупности может служить только репрезентативная выборка, правильно отражающая свойства генеральной совокупности. Это достигается методом случайного отбора элементов генеральной совокупности, при котором у всех ее элементов имеются равные шансы попадания в выборку. Применение данного метода одинаково подходит и для изучения различных явлений и процессов современности, и для обработки данных проведенных ранее выборочных статистических исследований, таких как переписи. Кроме того, выборочный метод также находит применение при обработке данных естественных выборок, от которых остались лишь фрагментарно сохранившиеся данные. Так, довольно часто, к таковым частично сохранившимся данным относятся актовые материалы, документы текущего делопроизводства и отчетности. В зависимости от того, каким образом осуществляется отбор элементов совокупности в выборку, различают несколько видов выборочного обследования, в которых отбор может быть случайным, механическим, типическим и серийным. Случайным называется отбор, при котором все элементы генеральной совокупности имеют равную возможность быть отобранными, например, с помощью жребия или таблицы случайных чисел. Способ жеребьевки применяется в том случае, если число элементов всей изучаемой совокупности невелико. При большом объеме данных осуществление случайного отбора при помощи жеребьевки становится сложным. Более пригоден, в случае большого объема обрабатываемых данных, метод использования таблицы случайных чисел. Способ отбора с помощью таблицы случайных чисел можно рассмотреть на следующем примере. Допустим, что совокупность состоит из 900 элементов, а намеченный объем выборки равен 20 единицам. В таком случае из таблицы случайных чисел следует отбирать числа, не превосходящие 900, до тех пор, пока не будут набраны требуемые 20 чисел. Выписанные числа следует считать порядковыми номерами попавших в выборку элементов генеральной совокупности. Для очень больших совокупностей лучше применить механический отбор. Так, при формировании 10%-ной выборки из каждых десяти элементов выбирается только один, а вся совокупность условно разбивается на равные части по 10 элементов. Далее из первой десятки наугад выбирается какой-либо элемент (например, при помощи жеребьевки). Остальные элементы выборки определяются указанной пропорцией отбора N номером первого отобранного элемента. Еще одним видом направленного отбора является типический отбор, когда совокупность разбивается на группы, однородные в качественном отношении. Только после этого уже внутри каждой группы производится случайный отбор. Хотя это более сложный метод, он дает более точные результаты. Серийный отбор представляет собой вид случайного или механического отбора, осуществляемый для укрупненных элементов исходной совокупности, которая в ходе анализа разбивается на группы (серии). Изложенные выше способы формирования выборок не исчерпывают собой всех типов отбора, применяемых на практике. В качестве примера применения выборочного метода в историографии рассмотрим подробнее проведенный отечественными исследователями анализ движения хлебных цен в России в XVIII веке. Была поставлена задача определить средние цены на хлеб по отдельным губерниям, районам и по России в целом за каждый год XVIII века, а также выявить динамику хлебных цен за столетие. Однако, в ходе исследования стало понятно, что составить таблицы с непрерывным рядом цен не удастся, так как данные в различных архивах сохранились лишь частично. Например, данные за 1708 год имелись только по 36 уездам страны. Только за периоды с 1744 по 1773 и с 1796 по 1801 годы сохранились данные по большинству городов России. В связи с этим было принято решение использовать в исследовании аппарат математической статистики, а именно, понятие среднего значения, дисперсии, среднего квадратического отклонения, доверительного интервала. В связи с разрозненностью имеющихся сведений из генеральной совокупности (все сохранившихся и несохранившихся данных о хлебных ценах за 1708 год) была произведена выборка, отражающая совокупность сохранившихся сведений о хлебных ценах. На основании данной выборки была рассчитана средняя цена на хлеб, а также показатель отклонения от среднего значения и был построен доверительный интервал для среднего значения генеральной совокупности с вероятностью 0,95 по следующим данным:
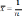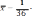   Среднее значение признака, которым является цена на хлеб в 1708 году, был найден по формуле: ∑ , где - n объем выборки. Из имеющихся данных следует, что 37,1копСреднее квадратическое (стандартное) отклонение было найдено по формуле 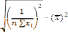    Таким образом, согласно данным выборки средняя цена на хлеб в России в 1708 году составляла 37 копеек со стандартным отклонением 16 копеек. Рассчитав коэффициент вариации, стало ясно, что выборка является неоднородной, вследствие чего возникла необходимость проведения дополнительного анализа цен на хлеб по районам. Нужно было выяснить, насколько средние цены на хлеб, вычисленные по данным выборки, могли отличаться от действительных средних хлебных цен, которые были бы получены, если бы в распоряжении оказались данные за этот год по всем уездам России. Соответственно была определена средняя и предельная ошибки выборки, и построен доверительный интервал. Средняя ошибка для повторной выборки была вычислена по формуле: 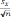  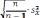  , где (исправленное среднее квадратическое отклонение). При подставлении данных, получаем 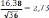  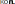  Предельная ошибка вычисляется по формуле: Δ =t*μ, где значение t зависит от значения вероятности, с которым строится доверительный интервал. При p = 0,95 имеем t = 1,96. Таким образом, получаем Δ = 1,96 2,37 = 5,35 коп.Далее были проведены вычисления по формуле доверительного интервала: хв— Δ < хген < хв + Δ. Было выяснено с вероятностью 95%, что средняя цена на хлеб в 1708 году по России могла изменяться в пределах от 31,75 копеек до 42,45 копеек. Таким образом, при помощи аппарата математической статистики, исследователям удалось вычислить средние цены по 10 районам России, а также среднероссийские цены за каждый год XVIII века. |