Матем. моделирование кредитов. Математическое моделирование_кредиты. Математическое моделирование

• Название: Математическое моделирование
• Анкор: Матем. моделирование кредитов
• Дата: 03.12.2020
• Размер: 21.08 Kb.
• Имя файла: Математическое моделирование_кредиты.docx
• Тип: Документы; #156369

6. Математическое моделирование

При выполнении этой работы можно использовать шаблон – электронную таблицу в файле Кредит.xls.

Уровень A.

1. 
   Дядя Ваня решил взять кредит 100 тыс. рублей в банке на год под 13% годовых. Банк предложил ему выплачивать каждый месяц равные суммы (такой платёж называется аннуитетным). Сумма ежемесячной выплаты p вычисляется по формуле: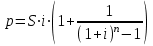
   

,

где S – сумма кредита, i – годовая процентная ставка кредита, делённая на 12; n – число месяцев, в течение которых нужно выплатить кредит.

Используя электронную таблицу или программу на языке программирования, определите, сколько всего денег выплатит дядя Ваня банку по процентам (сверх 100 тыс. рублей).

Ответ:

7180,73р.

Уровень B.

2. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня выплатит по процентам не более 10000 руб.
   

Ответ:

17,9%

Какова в этом случае будет величина ежемесячной выплаты:

9 163,24р.

3. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня будет ежемесячно выплачивать не более 9100 руб.
   

Ответ:

16,3%

Какова в этом случае будет общая сумма выплат:

109 047,46р.

Уровень С.

4. 
   Существует ещё один вариант выплаты кредита, при котором выплачиваемая сумма изменяется (уменьшается) каждый месяц. Такая схема называется дифференцированными платежами. Выплаты за текущий месяц складываются из двух частей – выплат p₁ за основную часть кредита (100 тыс. руб) и выплат по процентам p₂.
   

Первая часть, p₁, всегда постоянна и определяется как сумму кредита, делённая на количество месяцев. Для примеры, который рассмотрен в начале описания этой работы,

p₁ = 100000 : 12 = 8333,33 р.

Вторая часть, p₂, зависит от номера месяца k, поэтому будем обозначать её как p_2k. Она вычисляется как оставшаяся сумма основного долга, умноженная на годовую процентную ставку кредита, делённую на 12: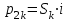



Например, в первый месяц выплат 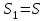(выплат ещё не было), поэтому

p₂₁ = 100000  0,13 / 12 = 1083,33 р.

Во второй месяц оставшаяся сумма долга равна

S₁ = 100000 – 8333,33 = 91666,67 р.

При этом получается другая выплата по процентам:

p₂₂ = 91666,67  0,13 / 12 = 993,06 р.

5. 
   
   При ставке 13% постройте график выплат дяди Вани при дифференцированных платежах. Сколько всего денег он переплатит по процентам?
   

Ответ:

7 041,67р.

Какой способ выплат выгоднее для дяди Вани:

дифференцированный

6. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня выплатит по процентам не более 10000 руб.
   

Ответ:

18,4%

Какова в этом случае будет величина выплаты в первый месяц:

9 866,67р.

7. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня будет ежемесячно выплачивать не более 9100 руб.
   

Ответ:

16,8%

Какова в этом случае будет общая сумма выплат:

109 100,00р.