Математика В 1. Математика. Базовый уровень. Тренировочный

• Название: Математика. Базовый уровень. Тренировочный
• Дата: 07.09.2022
• Размер: 228.96 Kb.
• Имя файла: Математика В 1.docx
• Тип: Документы; #666861
• страница: 2 из 3

 

В таблице под каждой буквой, соответствующей величине, укажи номер её возможного значения.

 

А Б В Г

Шаги решения

В порядке возрастания величины расположатся так:

 

толщина листа бумаги; рост человека; длина железнодорожного состава; расстояние от Москвы до Минска.

 

Сопоставив в возрастающем порядке числовые значения, получим:

 

А	Б	В	Г
3	4	2	1

4.  Задание 4  (1 Б.)

В таблице представлены результаты соревнований по прыжкам в длину с места.

 

Спортсмен	1-я попытка, см	2-я попытка,  см	3-я попытка, см	4-я попытка,  см	5-я попытка, см
Зайцев	193	198	194	194	186
Петров	187	187	198	200	198
Климов	197	196	184	193	193
Чуев	191	189	186	192	191

 

Каков результат лучшей попытки (в сантиметрах) спортсмена, занявшего четвёртое место?

 

Ответ:

192

.

Шаги решения

Чтобы ответить на вопрос задачи, нужно из пяти результатов каждого спортсмена выбрать наибольший.

 

Меньшее число из этих значений и будет результатом спортсмена, занявшего четвёртое место.

 

Это значение — 192.

5.  Задание 5  (1 Б.)

План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м ×  1 м. Найди площадь парка, изображённого на плане. Ответ дай в квадратных метрах.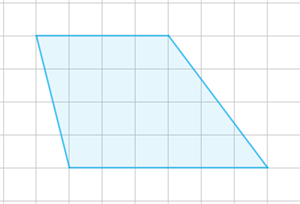

 



 

Рис. 1. Парк на плане местности

 

Ответ:

20

.

 

(В окошко пиши только число.)

Шаги решения

Парк на плане местности имеет форму трапеции. Проведём в трапеции высоту и вычислим её площадь.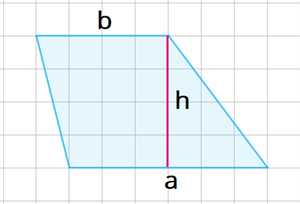

 



 

Рис. 2.Трапеция, высота трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.

S=a+b2⋅h;

 

S=4+62⋅4=20 м².

 

Правильный ответ: 20.

Источники:

Рис.1. Парк на плане местности. © ЯКласс.
Рис. 2. Трапеция, высота трапеции. © ЯКласс.  

6.  Задание 6  (1 Б.)

В марте завод увеличил выпуск продукции на 20%, а в апреле — на 10%. Определи объём произведённой в апреле продукции, если в феврале было выпущено 180000 единиц.

 

Ответ:

237600

.

Шаги решения

Найдём 20% от 180000:

 

180000⋅20100=36000;

 

180000+36000=216000.

 

Найдём 10% от 216000:

 

216000⋅10100=21600;

 

216000+21600=237600.

7.  Задание 7  (1 Б.)

Найди значение выражения  (15−−√−27−−√)(15−−√+27−−√).

 

Ответ:

-13

.

Шаги решения

Воспользуемся формулой разности квадратов:

 

(a−b)(a+b)=a2−b2.

 

(15−−√−27−−√)(15−−√+27−−√)=15−−√2−(27−−√)2=15−22⋅7=15−28=−13.

8.  Задание 8  (1 Б.)

Среднее геометрическое двух чисел вычисляется по формуле S=ab−−√. Найди среднее геометрическое чисел a=343 и b=175.

 

Ответ:

245

.

Шаги решения

S=343⋅175−−−−−−−√=72⋅7⋅52⋅7−−−−−−−−−−√=7⋅7⋅5=245.

9.  Задание 9  (1 Б.)

Найди корень уравнения (x−15)2=(x−14)2.

 

Ответ:

14,5

.

Шаги решения

Перенесём выражение из правой части в левую и применим формулу разности квадратов.

 

(x−15)2=(x−14)2;(x−15)2−(x−14)2=0;(x−15−(x−14))××(x−15+x−14)=0;(x−15−x+14)××(x−15+x−14)=0;−1(2x−29)=0;2x−29=0;2x=29;x=14,5.

10.  Задание 10  (1 Б.)

Прямоугольную площадку с размерами 10 м и 12 м требуется уложить плитками прямоугольной формы со сторонами 20 см и 10 см. Сколько потребуется таких плиток?

 

Ответ:

6000

.

Шаги решения

Подсчитаем количество плиток, которыми можно выложить 1 м2 площадки.

 

Например, мы можем разместить в один ряд по ширине 100:20=5 шт., а по длине — 100:10=10 шт.

 

Тогда всего потребуется 5⋅10=50 шт.,

 

так как площадь площадки 10⋅12=120 м².

 

Чтобы эту площадь выложить плиткой, потребуется

 

120⋅50=6000 штук.

11.  Задание 11  (1 Б.)

Из тысячи лампочек, поступивших в продажу, 78 бракованных. Какова вероятность того, что купленная лампочка исправна?

 

Ответ:

0,922

.

Шаги решения

Так как из тысячи лампочек бракованных 78, то исправных — 922.

 

Поэтому вероятность того, что лампочка исправна — 9221000=0,922.

12.  Задание 12  (1 Б.)

Для строительства дома планируется закупить 20 тонн кирпича. Предложения основных поставщиков представлены в таблице.

 

Поставщик	Цена кирпича (руб. за шт.)	Стоимость доставки (руб.)	Специальные условия
А	46	9000	Нет
Б	56	5000	Доставка бесплатно, если сумма заказа не менее 200000 руб.
В	64	3000	Доставка со скидкой 50%, если сумма заказа  не менее 240000 руб.

 

Во сколько рублей обойдётся самым дешёвым вариант покупки вместе с доставкой , если один кирпич весит 5 кг?

 

Ответ:

193000

.

Шаги решения

Подсчитаем, какое количество кирпича нужно купить:

 

200005=4000.

 

При заказе у поставщика «А» стоимость заказа с доставкой будет

 

46⋅4000+9000=193000.

 

При заказе у поставщика «Б» стоимость заказа с доставкой будет

 

56⋅4000=224000.

 

При заказе у поставщика «В» стоимость заказа с доставкой будет

 

64⋅4000+30002=257500.

 

Наименьшая сумма заказа — 193000 руб.

 

Источники:

https://base.mathege.ru/clones/?position=13&parent=9386

13.  Задание 13  (1 Б.)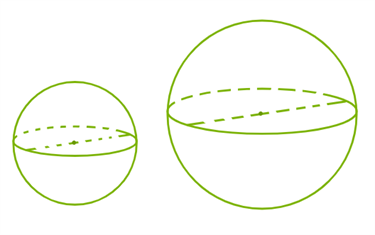



 

Масса металлического шара диаметром 4 см — 230,4 грам­м(-а).

 

Определи массу шара, из­го­тов­лен­но­го из того же металла, диа­мет­ром 1 см.

 

Ответ:

3,6

.

Шаги решения

Пусть m1, V1, d1, r1 — соответственно масса, объём, диаметр и радиус первого шара, а m2, V2, d2, r2 — соответственно масса, объём, диаметр и радиус второго шара.

 

m1m2=V1V2=r13r23=d13d23;

 

230,4m2=4313;

 

m2=230,4⋅1343=3,6⋅13=3,6.

14.  Задание 14  (1 Б.)

Установи соответствие между функциями и характеристиками этих функций на отрезке [0;9].

 

ФУНКЦИИ	ХАРАКТЕРИСТИКИ
А) y=4x−6	1) функция имеет точку максимума на отрезке[0;9]
Б) y=x2−x+8	2) функция возрастает на отрезке [0;9]
В) y=5x−x2	3) функция убывает на отрезке[0;9]
Г) y=6−3x	4) функция имеет точку минимума на отрезке  [0;9]

 

А Б В Г

 

Источники:

https://base.mathege.ru/prototypes/?position=15

Шаги решения

Функция y=4x−6 возрастающая, так как 4>0.  Поэтому ей подходит вариант А→2.

 

Функция y=x2−x+8 имеет точку минимума, так как ветви параболы направлены вверх (a>0). Поэтому ей подходит вариант Б→4.  

 

Функция y=5x−x2 имеет точку максимума, так как ветви параболы направлены вниз (a<0).  Поэтому ей подходит вариант В→1.  

 

Функция y=6−3x убывающая, так как −3<0.  Поэтому ей подходит вариант Г→3.

 

А	Б	В	Г
2	4	1	3

Источники:

 

https://base.mathege.ru/prototypes/?position=15

15.  Задание 15  (1 Б.)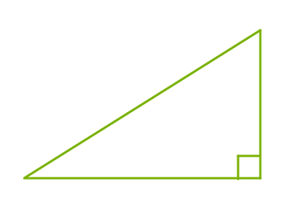



 

Найди площадь прямоугольного треугольника, если его гипотенуза равна 106−−−√, а один из катетов равен 5.

 

Ответ:

22,5

.

Шаги решения

Катет треугольника с катетами a и b и гипотенузой c можно найти по теореме Пифагора:

 

a2=c2−b2.

 

106−52−−−−−−−√=9.

 

Площадь треугольника найдём по формуле:

 

S=ab2.

 

S=5⋅92=22,5.

16.  Задание 16  (1 Б.)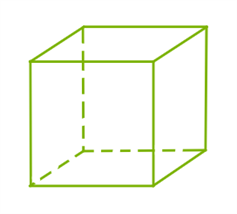



 

Два ребра прямоугольного параллелепипеда равны 3 и 5, а объём равен 45. Найди площадь поверхности этого параллелепипеда.

 

Ответ:

78

.

Шаги решения

V=abc;

 

c=Vab;

 

c=453⋅5=3.

 

Грани параллелепипеда попарно равны, поэтому площадь поверхности равна удвоенной сумме площадей граней:

 

S=2⋅(ab+bc+ac);

 

S=2⋅(3⋅5+5⋅3+3⋅3);

 

S=78.

17.  Задание 17  (1 Б.)

Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установи соответствие между числами и отрезками из правого столбца.

 

ЧИСЛА	ОТРЕЗКИ
А)  log3217	1) [4;5]
Б)   75	2) [1;2]
В)   15−−√	3) [2;3]
Г)  0,37−1	4) [3;4]

 

Впиши в приведённую в ответе таблицу под каждой буквой соответствующую цифру.

 

А Б В Г

Шаги решения

Так как

 

log334<log3217<log335;log381<log3217<log3243.

 

Выбираем А→1.

 

Так как 55<75<2⋅55, выбираем Б→2.

 

Так как 32−−√<15−−√<42−−√, выбираем В→4.

 

Так как

 

0,37−1=10037;10050<10037<3⋅3737.

 

Выбираем Г→3.

 

 

А	Б	В	Г
1	2	4	3

 

Источники:

https://base.mathege.ru/prototypes/?position=18

18.  Задание 18  (1 Б.)

Среди 24 сотрудников фирмы 14 являются абонентами сети МТС, а 15 — Мегафон.

 

Выбери верные утверждения (запиши номера ответов без пробелов и знаков препинания):

 

1) среди сотрудников фирмы найдутся хотя бы 5, которые являются абонентами и сети МТС, и сети Мегафон.

 

2) Найдётся 14 человек среди этих сотрудников фирмы, которые не являются абонентами ни одной, ни другой сети.

 

3) Не более 14 человек из сотрудников компании пользуются обеими сетями.

 

4) Среди этих сотрудников не найдётся ни одного человека, который являлся бы абонентом только сети МТС.

 

Ответ: 

13

.

Шаги решения

1) Утверждение верно, так как если среди 24 сотрудников 14 являются только абонентами сети МТС, то абонентами сети Мегафон были бы 10 человек, а так как их 15, то 5 сотрудников пользуются обеими сетями.

 

2) Утверждение неверно, так как минимум 15 сотрудников пользуются какой-то сетью. Тогда не пользоваться ни одной из сетей могут максимум 9.

 

3) Утверждение верно, так как это число не может превышать 14.

 

4) Утверждение неверно. Если, например, 14 сотрудников пользуются обеими сетями, то 9 человек ни одной из указанных сетей не пользуются.

19.  Задание 19  (1 Б.)

Вычеркни в числе 81457625 три цифры так, чтобы получившееся число делилось на 18.

В ответе укажи какое-нибудь одно получившееся число.

 

Ответ:

84762

.

Шаги решения

Так как число делится на 18, оно должно делиться на 9 и быть чётным.

 

Значит, вычёркиваем последнюю цифру, так как она нечётная.

 

Чтобы число делилось на 9, нужно, чтобы сумма цифр делилась на 9. Сумма оставшихся цифр — 33. Значит, нужно вычеркнуть две цифры суммой 6 или 15. Это 4 и 2, 5 и 1 или 7 и 8.

 

Возможные варианты:

 

84762,

 

81576,

 

14562.

Источники:

https://base.mathege.ru/clones/?position=20&parent=1398

20.  Задание 20  (1 Б.)

Автомобиль выехал с постоянной скоростью 75 км/ч из города A в город B, расстояние между которыми равно 250 км. Одновременно с ним из города C в город B, расстояние между которыми равно 225 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 20 минут. В результате автомобиль и мотоцикл прибыли в город B одновременно. Найди скорость мотоциклиста. Ответ дай в км/ч.

 

Ответ:

75

.

Шаги решения

Пусть скорость мотоциклиста — x. Внесём известные данные в таблицу.

 

	Скорость, км/ч	Время, ч.	Расстояние, км
Автомобиль	75	25075	250
Мотоцикл	x	25075−2060=93	225

 

v2=St2=225⋅39=75 км/ч.