МАТЕМАТИКО-СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДЕЯТЕЛЬНОСТИ ПРОТИВОПОЖА. математикостатистическое моделирование деятельности противопожарной службы города
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
|
МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ ПО ДЕЛАМ ГРАЖДАНСКОЙ ОБОРОНЫ, ЧРЕЗВЫЧАЙНЫМ СИТУАЦИЯМ И ЛИКВИДАЦИИ ПОСЛЕДСТВИЙ СТИХИЙНЫХ БЕДСТВИЙ Академия Государственной противопожарной службы Кафедра организации деятельности пожарной охраны Курсовая работа по дисциплине «Математические методы и модели управления пожарно-спасательными службами» Тема: «МАТЕМАТИКО-СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДЕЯТЕЛЬНОСТИ ПРОТИВОПОЖАРНОЙ СЛУЖБЫ ГОРОДА»
Москва 2023
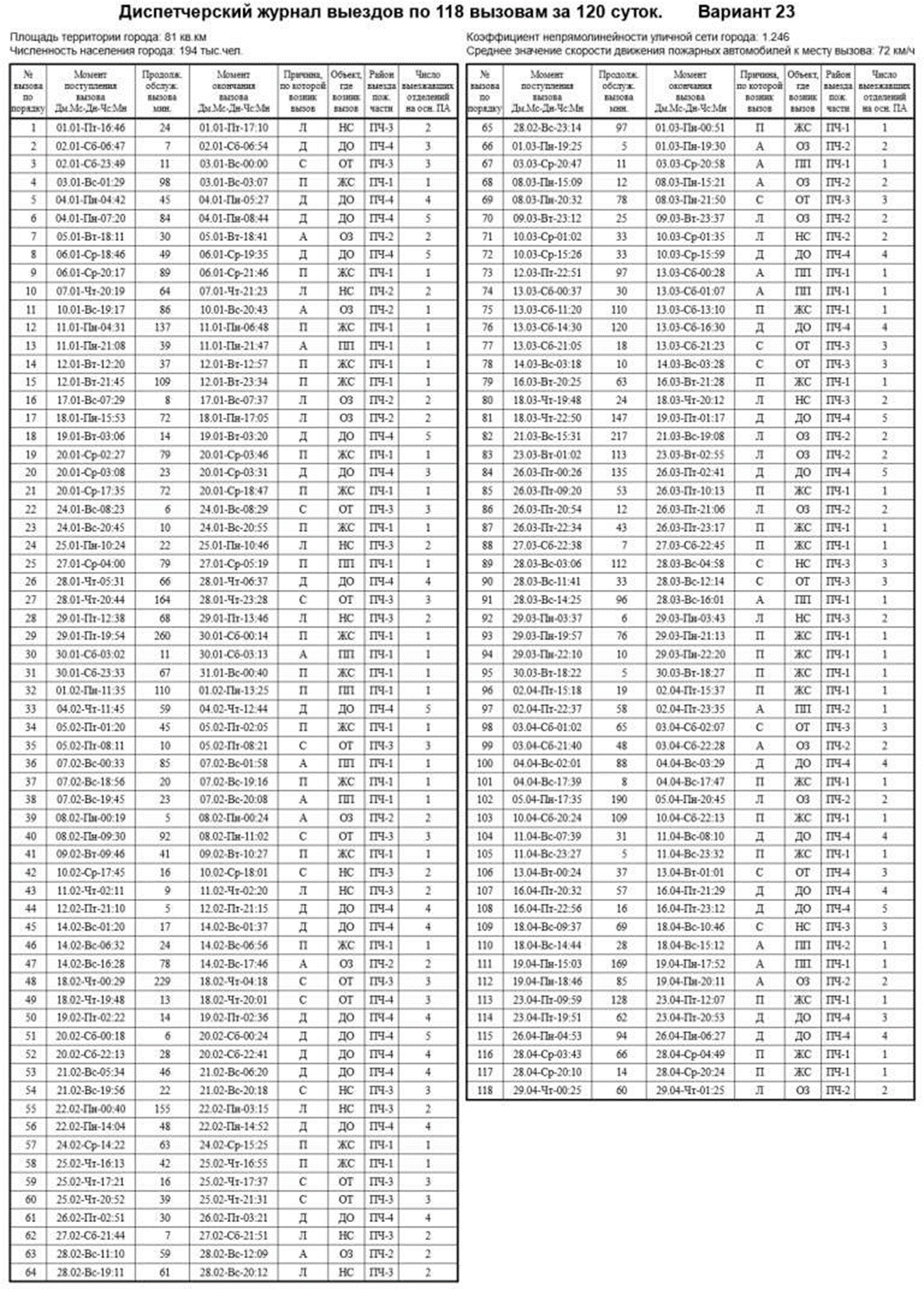 Введение Проблемы обеспечения пожарной безопасности, в данный момент, становятся все более актуальными и сложными. Основные резервы повышения эффективности деятельности пожарно-спасательных служб необходимо искать в совершенствовании организации управления, и более широком привлечении общественности к обеспечению безопасности народного хозяйства страны. Принцип научности управления в сфере пожарной охраны требует изучения закономерностей процесса функционирования пожарной охраны и управления ее аппаратами и подразделениями, творческого использования этих закономерностей при рационализации существующих и разработке новых структур управления, организации процесса управления, подбора и расстановки кадров. Совершенствование организации и управления пожарно-спасательных служб предполагает предварительную, глубокую научную проработку, по возможности, всех организационно-управленческих проблем, которые практика во всевозрастающих масштабах ставит перед работниками пожарной охраны. Современные нормативные положения и рекомендации пока еще далеки от совершенства и не получили научного обоснования, что значительно затрудняет решение, проблемы повышения эффективности деятельности Государственной противопожарной службы и совершенствования управления, ею. Для решения указанных и подобных им организационно-управленческих проблем необходимо развернуть комплексное научное исследование процесса функционирования пожарно-спасательных служб, включающее организационный, функциональный, территориальный и отраслевой аспекты этого процесса. Решение современных организационно-управленческих задач связано со сбором и обработкой огромных информационных массивов, с колоссальным объемом вычислений. Эту работу сейчас все успешнее выполняет новая вычислительная техника. Таким образом, математические методы решения организационно-управленческих проблем нужно рассматривать как весьма эффективные методы, которые, тем не менее, необходимо сочетать с другими методами, позволяющими в совокупности с первыми получить остаточно обоснованные и практически приемлемые решения таких проблем. Кроме того, известная ограниченность применения математических методов заключается в том, что любая математическая модель не в состоянии учесть все многообразие факторов и параметров, оказывающих существенное влияние на изучаемые процессы и явления. Достоверность полученных результатов при использовании математических методов управления зависит от правильности сделанных предпосылок и взятых за основу исходных данных. Цель курсовой работы – повышение эффективности деятельности пожарной охраны города. Задачи курсовой работы: 1. Анализ статистических закономерностей привлечения пожарной техники для обслуживания вызовов; 2. Анализ статистических закономерностей распределения числа вызовов пожарных подразделений в городе по суткам; 3. Анализ статистических закономерностей распределения длительности обслуживания вызовов пожарных подразделений в городе; 4. Моделирование одновременной занятости пожарных автомобилей при обслуживании вызовов в городе; 5. Обоснование числа пожарных автомобилей для обслуживания вызовов в городе на основании числа отказов в обслуживании вызовов. 1. Анализ статистических закономерностей привлечения пожарной техники для обслуживания вызовов П 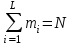 о данным диспетчерского журнала находим число mi вызовов о данным диспетчерского журнала находим число mi вызовов в городе, по которым выезжало определенное число i пожарных автомобилей (i = 1,2,...,L, где L - максимальное число выезжавших по вызову пожарных автомобилей). Для полученных значений mi, называемых абсолютными частотами, должно выполняться соотношение: где N – общее число вызовов. Производим вычисление доли ωi, которую в общем числе вызовов составляют вызовы, для обслуживания которых привлекались i пожарных автомобилей (i = 1, 2,...,L):  Для полученных в результате вычислений значений ωi (i = 1,2,…,L), называемых относительными частотами или частостями, должно выполняться соотношение: 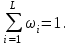 Перечень различных значений числа i выезжавших по вызову пожарных автомобилей (i = 1,2,...,L), каждому из которых поставлено в соответствие значение частоты mi и частости ωi, образует дискретный вариационный ряд, представленный в виде табл.1. О 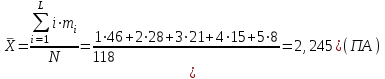 пределим статистические характеристики данного вариационного ряда. Находим среднее число одновременно выезжающих пожарных автомобилей пределим статистические характеристики данного вариационного ряда. Находим среднее число одновременно выезжающих пожарных автомобилей по вызову (для представленного варианта): Н 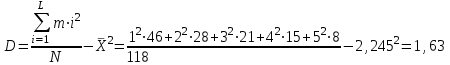 аходим дисперсию вариационного ряда: аходим дисперсию вариационного ряда:Н 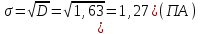 аходим среднее квадратическое отклонение: аходим среднее квадратическое отклонение:и 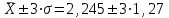 спользуя правило «трех сигм», получаем спользуя правило «трех сигм», получаемоткуда следует, что размах вариаций будет находиться в пределах от 0 до 6,05 автомобилей, выезжающих по вызову. Для графического отображения распределения i выезжавших по вызову пожарных автомобилей в городе производится построение секторной круговой диаграммы (рис.1). Для построения диаграммы на круге произвольного диаметра с помощью транспортира выделяют секторы с центральными углами φi (i = 1,2,…,L), пропорциональными относительным частотам ωi. Центральные углы вычисляются по формуле: При этом достаточно ограничиться целыми значениями, так как при помощи транспортира затруднительно добиться точности до долей градуса. Полученные значения центральных углов вносятся в табл. 1. Для них должно выполняться соотношение: 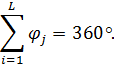 Таблица 1 Распределение числа пожарных автомобилей, выезжающих по вызовам
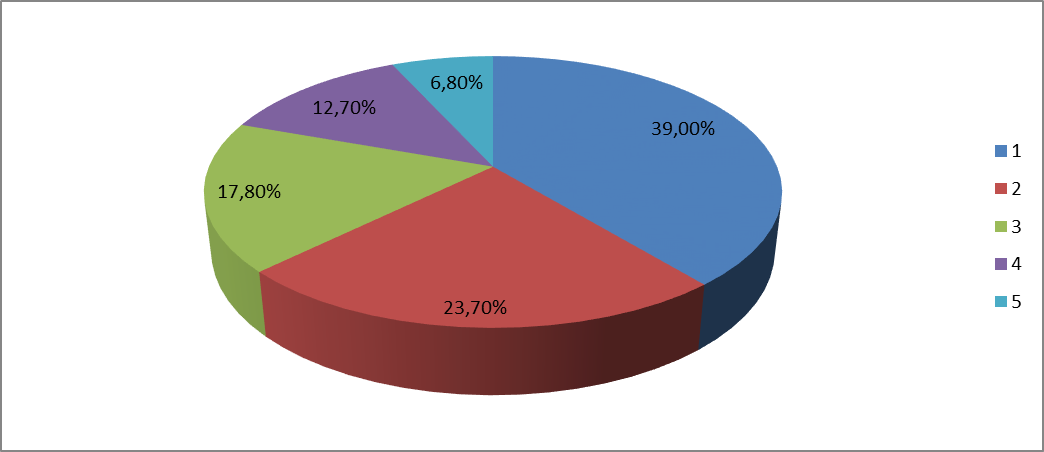 Рис.1 Секторная круговая диаграмма распределения числа пожарных автомобилей, выезжающих по вызовам Выводы: на большинство вызовов выезжают 1 (39 %) и 2 (23,7 %) пожарных автомобилей. 2. Анализ статистических закономерностей распределения числа вызовов пожарных подразделений в городе по суткам В течение периода наблюдения, зафиксированного в диспетчерском журнале и равного 120 суткам, определим эмпирическое и теоретическое распределение вызовов по суткам. Для определения эмпирического распределения необходимо сделать следующее: по диспетчерскому журналу подсчитать число mk суток с определенным числом вызовов k (k = 0,1,2,…n). Вызовы, возникающие в течение одних суток, имеют одинаковые даты поступления. Для определения значения m0 нужно посчитать число суток, даты которых отсутствуют в диспетчерском журнале, т.е. в эти сутки не произошло ни одного вызова. П 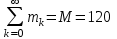 олученные в результате подсчетов значения mk называются эмпирическими частотами и связаны между собой соотношением: олученные в результате подсчетов значения mk называются эмпирическими частотами и связаны между собой соотношением:Э 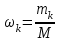 мпирическая вероятность ωk (относительная частота) того, что в интервале времени равным 1 суткам в городе произойдет k вызовов, оценивается как доля, которую в общем числе M суток составляет число суток, в течение которых произошло k вызовов: мпирическая вероятность ωk (относительная частота) того, что в интервале времени равным 1 суткам в городе произойдет k вызовов, оценивается как доля, которую в общем числе M суток составляет число суток, в течение которых произошло k вызовов:Д 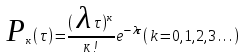 ля определения теоретической вероятности того, что за время τ произойдет k выездов пожарных подразделений используем распределение Пуассона: ля определения теоретической вероятности того, что за время τ произойдет k выездов пожарных подразделений используем распределение Пуассона:где λ – плотность потока вызовов, т.е. среднее число вызовов, поступающих за единицу времени τ, для нашего варианта λ=N/M=118/120=0,998 выз./сутки. Проведем ряд расчетов теоретической вероятности для примерного варианта: 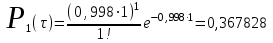 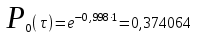 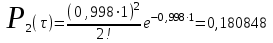 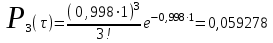 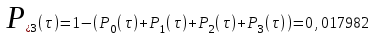 Д 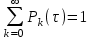 ля любого фиксированного значения τ вероятности Pk(τ), соответствующие значениям k = 0,1,2,… связаны между собой следующим соотношением ля любого фиксированного значения τ вероятности Pk(τ), соответствующие значениям k = 0,1,2,… связаны между собой следующим соотношениемНаходим распределение теоретических частот fk выездов k пожарных подразделений по суткам по следующей формуле: Проведем расчет теоретических частот для примерного варианта 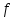 0 = 120·0,374064 = 44,9 0 = 120·0,374064 = 44,9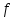 1 = 120·0,367828 = 44,1 1 = 120·0,367828 = 44,1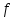 2 = 120·0,180848 = 21,7 2 = 120·0,180848 = 21,7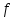 3 = 120·0,059278 = 7,1 3 = 120·0,059278 = 7,1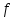 >3 = 120-(44,9+44,1+21,7+7,1) = 2,2 >3 = 120-(44,9+44,1+21,7+7,1) = 2,2Визуальное сопоставление полигонов эмпирического и теоретического распределений позволяет сделать вывод о сходстве характеров рассматриваемых распределений. Более точное заключение можно сделать, если использовать статистический критерий согласия Романовского: 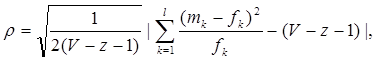 где V – число групп значений случайной величины, для каждой из которых должно выполняться условие fk ≥ 9, если для какой-либо k-ой группы это условие не выполняется, то эта группа объединяется с предыдущей или с последующей группой, а соответствующие им частоты складываются, для нашего примера V = 3; z – число параметров закона распределения, для закона Пуассона и для показательного закона z = 1. Если значение критерия Романовского ρ < 3, то расхождения можно считать не существенными (случайными), если ρ ≥ 3 – существенными. Для нашего примера: ρ= 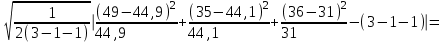 0,51 0,51Расчетное значение ρ = 0,51 не превышает значения 3, т.е. расхождения между эмпирическим и теоретическим распределениями можно считать не существенными. Таким образом, закон Пуассона целесообразно использовать для вероятностных расчетов распределения числа вызовов на различных временных интервалах. Таблица 2 Эмпирическое и теоретическое распределения числа вызовов пожарных подразделений в городе в интервале времени продолжительностью 1 сутки
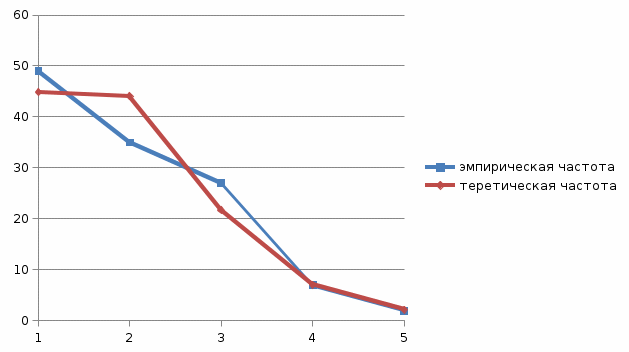 Рис.2 Полигон частот эмпирического и теоретического распределений числа вызовов пожарных подразделений в городе в интервале времени продолжительностью 1 сутки 3. Анализ статистических закономерностей распределения длительности обслуживания вызовов пожарных подразделений в городе Определим 5 групп (V) со следующими границами интервалов времени [0,30), [30,60), [60,90), [90,120), [120, ∞). Для определения эмпирического распределения необходимо сделать следующее: по диспетчерскому журналу подсчитать число mj вызовов, у которых длительность времени обслуживания τобсл. попадает в j-й интервал. П 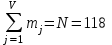 олученные в результате подсчетов значения mj называются эмпирическими частотами и связаны между собой соотношением: олученные в результате подсчетов значения mj называются эмпирическими частотами и связаны между собой соотношением:Э 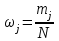 мпирическая вероятность ωj (относительная частота) того, что τобсл попадет в j-й интервал, оценивается как доля, которую в общем числе N вызовов составляют вызовы, попавшие в j-й интервал: мпирическая вероятность ωj (относительная частота) того, что τобсл попадет в j-й интервал, оценивается как доля, которую в общем числе N вызовов составляют вызовы, попавшие в j-й интервал:Д 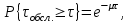 ля определения теоретической вероятности pj того, что ля определения теоретической вероятности pj того, что значение τобсл окажется меньше или больше какого-либо значения τ или попадет в j-й интервал используем показательное распределение 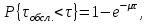 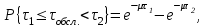 где µ - параметр показательного закона распределения µ = 1/τср.обсл.. Средняя длительность времени обслуживания τср.обсл. может быть вычислена двумя способами: 1 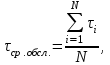 ) как среднее арифметическое: ) как среднее арифметическое:где τi – длительность времени обслуживания i-ого вызова, для нашего примера τср.обсл. = 57,5 мин; 2 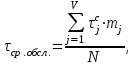 ) как среднее арифметическое взвешенное: ) как среднее арифметическое взвешенное:где 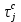 - середина j-ого интервала, для нашего примера τср.обсл. = 57,7 мин. - середина j-ого интервала, для нашего примера τср.обсл. = 57,7 мин.Среднее арифметическое взвешенное является менее точным, чем простое арифметическое, но для его нахождения требуется меньший объем вычислений. П 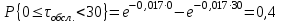 роведем расчет теоретической вероятности для примерного варианта. роведем расчет теоретической вероятности для примерного варианта.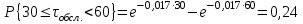 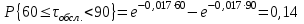 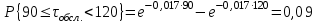 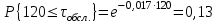 Далее, для каждого j-ого интервала определяем теоретическую частоту fj вызовов, длительность времени обслуживания которых находится в пределах границ j-ого интервала. 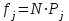 Проведем необходимые вычисления теоретической частоты для примерного варианта: 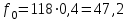 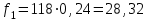 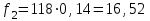 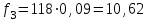 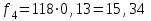 Результаты расчетов заносим в таблицу 3. Визуальное сопоставление полигонов эмпирического и теоретического распределений позволяет сделать вывод о сходстве характеров рассматриваемых распределений. Для более точного заключения определим статистический критерий согласия Романовского, расчеты критерия производятся по примеру задания 2. Для примерного варианта имеем ρ = 0,12. Поскольку расчетное значение не превышает значения 3, расхождения между эмпирическим и теоретическим распределениями можно считать не существенными и считать, что в данном случае время обслуживания вызовов ПП подчиняется показательному закону распределения. Таблица 3 Эмпирическое и теоретическое распределения длительности времени обслуживания вызовов пожарными подразделениями в городе
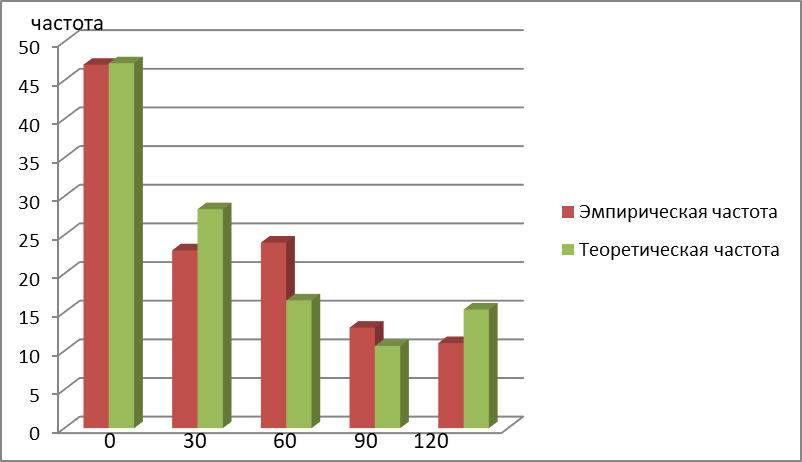 Время, τ мин. Рис.3 Гистограмма эмпирического и теоретического распределений длительности времени обслуживания вызовов пожарными подразделениями в городе 4. Моделирование одновременной занятости пожарных автомобилей при обслуживании вызовов в городе Д 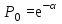 ля определения вероятности Pk того, что в произвольный момент времени обслуживанием вызовов в городе будут одновременно заняты k пожарных автомобилей, используем следующие формулы: ля определения вероятности Pk того, что в произвольный момент времени обслуживанием вызовов в городе будут одновременно заняты k пожарных автомобилей, используем следующие формулы: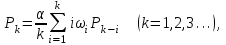 где α – приведенная плотность потока вызовов в городе, которая определяется как ωi – относительная частота привлечения iпожарных автомобилей для обслуживания вызовов берем из раздела 1. П 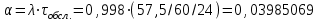 роведем ряд вычислений для примерного варианта (учитывая размерность величин λ и τ): роведем ряд вычислений для примерного варианта (учитывая размерность величин λ и τ):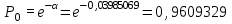 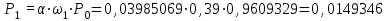 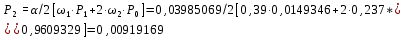 Аналогичным образом определяем значения: P3=0,03985069/3*(0,39*0,00919169+2*0,237*0,0149346+3*0,178*0,99609329) = 0,00695795; P4 = 0,03985069/4*(0,39*0,00695795+2*0,237*0,00919169+3*0,178*0,0149346++4*0,127*0,99609329) = 0,00484415; P5 = 1-(0,9609329+0,0149346+0,00919169+0,00695795+0,00484415) =0,00313871. Значения вероятностей Pkдля k = 0,1,2,.. связаны соотношением: 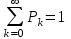 Д 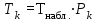 алее определяем суммарную продолжительность времени Tkпребывания алее определяем суммарную продолжительность времени Tkпребывания в ситуации k за период наблюдения Tнабл. = 120 суток. З 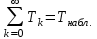 начения Tk для k = 0,1,2,.. связаны соотношением: начения Tk для k = 0,1,2,.. связаны соотношением:Ч 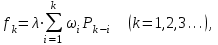 астота fk– среднее число случаев нахождения в ситуации kвычисляется по формуле: астота fk– среднее число случаев нахождения в ситуации kвычисляется по формуле:где λ – число вызовов за период наблюдения, т.е. λ=N. П 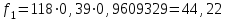 роведем ряд вычислений для примерного варианта: роведем ряд вычислений для примерного варианта: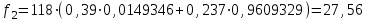 Аналогичным образом определяем значения: f3 = 118*(0,39*0,00919169+0,237*0,0149346+0,178*0,9609329) = 21,02; f4 = 118*(0,39*0,00695795+0,237*0,00919169+0,178*0,0149346+0,127*0,9609329) = =15,29; f5 = 118-(44,22+27,56+21,02+15,29) = 9,91 З 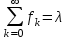 начения fk для k = 0,1,2,.. связаны соотношением: начения fk для k = 0,1,2,.. связаны соотношением:Результаты всех расчетов представлены в табл.4 Таблица 4 Теоретические значения характеристик одновременной занятости того или иного числа k пожарных автомобилей обслуживанием вызовов в городе
По результатам расчетов примера можно сделать следующий вывод: в 98 % всего времени пожарные подразделения находятся в ситуации ожидания очередного вызова. 5. Обоснование числа пожарных автомобилей для обслуживания вызовов в городе на основании числа отказов в обслуживании вызовов Число пожарных автомобилей в городе должно быть достаточным для того, чтобы обеспечить безотказное обслуживание вызовов. Под отказом понимается событие, которое состоит в том, что по очередному вызову не может выехать требуемое число пожарных автомобилей вследствие их занятости на других вызовах. Отказ называется полным, если по вызову не может выехать ни один пожарный автомобиль. Отказ называется частичным, если по вызову может выехать число пожарных автомобилей, меньше требуемого для его обслуживания. В качестве критериев для обоснования числа n пожарных автомобилей для города используем вероятностные, временные и частотные характеристики безотказного обслуживания вызовов. Для этого будем использовать результаты предыдущего задания, в котором моделировалась одновременная занятость пожарных автомобилей. В 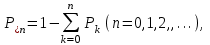 ероятность того, что в произвольный момент времени заданного ероятность того, что в произвольный момент времени заданного числа n пожарных автомобилей будет недостаточно для обслуживания вызовов вычисляется по формуле: где Pk – вероятность того, что в произвольный момент времени обслуживанием вызовов в городе одновременно занято k пожарных автомобилей, эти значения берем из раздела 4. П 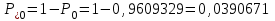 роизведем расчеты вероятности P>nдля примерного варианта. роизведем расчеты вероятности P>nдля примерного варианта.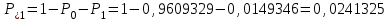 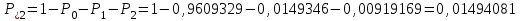 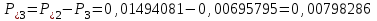 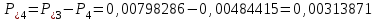 Далее, определим ожидаемую продолжительность времени нахождения в ситуации T>n, когда для обслуживания вызовов не хватит n пожарных автомобилей в течение периода наблюдения Tнабл.. 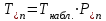 П 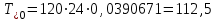 роизведем расчеты вероятности T>nдля примерного варианта. роизведем расчеты вероятности T>nдля примерного варианта.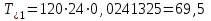 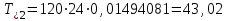 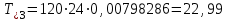 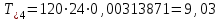 Частота возникновения отказов fотк.(n) в обслуживании вызовов в городе при заданном числе пожарных автомобилей n определяется по следующей формуле: 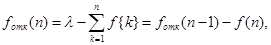 где fk– частота возникновения ситуации одновременной занятости kпожарных автомобилей (эти значения берем из раздела 4.). П 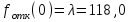 роизведем расчеты вероятности fотк.(n) для примерного варианта. роизведем расчеты вероятности fотк.(n) для примерного варианта.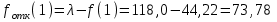 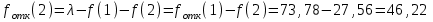 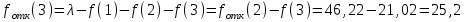 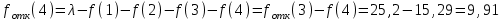 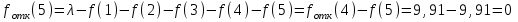 Частота возникновения полных отказов в обслуживании вызовов в городе при заданном числе n пожарных автомобилей вычисляется по формулам: (n = 1,2,3…) Частота возникновения частичных отказов в обслуживании вызовов в городе при заданном числе n пожарных автомобилей вычисляется по формуле: (n=1,2,3…) 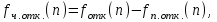 Все результаты расчетов представлены в табл.5. Таблица 5 Расчетные значения критериев для обоснования числа n пожарных автомобилей в городе
Выводы 1. В диспетчерском журнале нашли число mi вызовов в городе, по которым выезжало определенное число i пожарных автомобилей (i = 1,2,...,L, где L – максимальное число выезжавших по вызову пожарных автомобилей). На основании расчетов, получили следующий вывод относительно анализа статистических закономерностей привлечения пожарной техники для обслуживания вызовов: на большинство вызовов выезжают 1 (39 %) и 2 (23,7 %) пожарных автомобилей. 2. Расчетное значение ρ = 0,51 не превышает значения 3, т.е. расхождения между эмпирическим и теоретическим распределениями можно считать не существенными. Таким образом, закон Пуассона целесообразно использовать для вероятностных расчетов распределения числа вызовов на различных временных интервалах. 3. Визуальное сопоставление полигонов эмпирического и теоретического распределений позволяет сделать вывод о сходстве характеров рассматриваемых распределений. Для примерного варианта имеем ρ = 0,12. Поскольку расчетное значение не превышает значения 3, расхождения между эмпирическим и теоретическим распределениями можно считать не существенными и считать, что в данном случае время обслуживания вызовов ПП подчиняется показательному закону распределения. 4. По результатам расчетов примера можно сделать вывод, что в 96 % всего времени пожарные подразделения находятся в ситуации ожидания очередного вызова. 5. По результатам расчетов производится обоснование числа n пожарных автомобилей, обеспечивающих надежную противопожарную защиту города. Если для рассматриваемого примера в состав дежурных караулов городских ПЧ включить 4 пожарных автомобиля, то будет обеспечен весьма высокий уровень противопожарной защиты города: в течение рассматриваемого периода времени (120 суток) для обслуживания вызовов в городе потребуется привлечь дополнительные пожарные автомобили извне лишь в единичных случаях fотк(4) = 9,91. При этом суммарная продолжительность занятости дополнительных отделений обслуживанием вызовов в городе составит около 9 ч за год. Литература 1. Статистика . Под. Ред. В.Г. Ионина. Курс лекций: М- «Инфра –М» 1998. 2. Брушлинский Н.Н., С.В. Соколов Математические методы и модели управления в ГПС. Учебник. - М.: Академия МЧС России, 2011. -172 с. 3. Н.Н.Брушлинский, С.В.Соколов, Е.М.Алехин и др. Безопасность городов. Имитационное моделирование городских процессов и систем. – М.: ФАЗИС, 2004. – с.172. 4. Брушлинский Н.Н. Системный анализ деятельности Государственной противопожарной службы. - М.: МИПБ МВД России, 1998. - 255 с. 5. Коробко В.Б. Расширение функций Государственной противопожарной службы: вопросы теории и практики. - М.: Изд-во АРС, 2002. - 131 с. 6. Управление в государственной противопожарной службе: Альбом схем / B.C. Артамонов, Р.Н. Козленко, П.А. Смирнов: СПбИГПС, 2004. 7. Шикин Е.В., Чхартишвили А.Г. Математические модели и методы в управлении: Учебное пособие. - М.: Дело, 2002. 8. Экономико-математическое моделирование: Учебник / под общ. ред. И.Н. Дрогобыцкого. - М: Экзамен, 2006. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
