Матрица прямоугольная таблица чисел, содержащая m строк одинаковой длины или n столбцов одинаковой длины. Для каждой квадратной матрицы n ного порядка существует определитель nного порядка, элементы которого равны соответствующим элементам матриц Операции.
 Скачать 77.77 Kb. Скачать 77.77 Kb.
|
|
Ответы на вопросы для зачета по математике Матрица- прямоугольная таблица чисел, содержащая m строк одинаковой длины или n столбцов одинаковой длины. Для каждой квадратной матрицы n- ного порядка существует определитель n-ного порядка, элементы которого равны соответствующим элементам матриц Операции. Умножение матрицы на число: Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. Следствие: общий множитель всех элементов матрицы, можно вынести за знак матрицы Сложение матриц: Для выполнения сложения матриц, необходимо, чтобы они были одинаковыми по размеру. Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы Умножение матриц: Матрицы можно умножать, только в том случае, если число столбцов первой матрицы произведения равно числу строк второй. Произведение матриц равен сумме попарных произведений элемента, строки матрицы на соответствующие элементы столбцов матрицы. Вычисление определителя второго порядка: Определителем матрицей второго порядка называется число 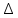 2, определяемое формулой: 2, определяемое формулой:  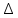 2 =|A|= а11; а12 = а11*а22-а12*а21 2 =|A|= а11; а12 = а11*а22-а12*а21а21; а22 Вычисления определителя третьего порядка: Определителем третьего порядка называется число 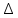 3 определяемое формулой: 3 определяемое формулой: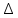 3=а11*а22*а33+а12*а23*а31+а13*а21*а32-а13*а22*а31-а11*а23*а32-а12*а21*а33 3=а11*а22*а33+а12*а23*а31+а13*а21*а32-а13*а22*а31-а11*а23*а32-а12*а21*а33Свойства определителей: Определитель не изменится, если все строки заменить соответствующими столбцами и наоборот При перестановке двух каких-либо строк или столбцов местами определитель изменяет знак Если определитель имеет две одинаковые строки или два одинаковых столбца, то он равен нулю Множитель, общий для всех элементов строки или столбца, можно выносить за знак определителя Если к элементам некоторой строки или столбца прибавить соответствующие элементы другой строки или столбца, то определитель не изменится Сумма произведений элементов какого-нибудь столбца или строки определителя на алгебраические дополнения соответствующих элементов другого столбца или строки равна нулю. Система линейных уравнений- объединение из n линейных уравнений, каждое из которых содержит k переменных. Матричная запись:    а11 а12 … а13 b1 x1 А= а21 а22 … а23 B= b2 x= x2 …. …. … …. … … ат1 аm2 … аmnbnxn  Пусть задана система n уравнений с n неизвестными: а11х1+ а12х2+…. + а1nxn = b1 а21х1+ а22х2+…. + а2nxn = b2 ………. + …… + ……. + ………. = …. аn1х1 + аn2x2 + …+ аnnxn = bn А- матрица этой системы, а В- столбец свободных членов    а11 а12 …. а1nb1 а11 а12 …. а1nb1А= а21 а22 … а2n В= b2 …. …… …. ….. …. аn1 аn2 …. Аnnbn  Если определитель матрицы системы Если определитель матрицы системы 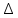 =det А =0, то системы линейный уравнений имеет единственное решение, которое вычисляется по формулам =det А =0, то системы линейный уравнений имеет единственное решение, которое вычисляется по формулам Хi= Хi= 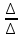 I , i= 1, n где I , i= 1, n где 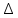 i- определители матриц, которые получаются из матрицы i- определители матриц, которые получаются из матрицы А заменой i-го столбца на столбец свободных членов B. Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается х1 из всех уравнений системы, начиная со второго, далее исключается х2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная хn. Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находится xn с помощью этого значения из предпоследнего уравнения вычисляется xn-1, и так далее, из первого уравнения находится x1. Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса.  Дана система а11х1 + а12х2-а13х3 = b1 а21х1 – а22х2 + а23х3 = b2 а31х1 + а33х3 = b3     а11 а12 а13 b1 а11 а12 а13 b1A= а21 а22 а23 B= b2  а31 …. а33 b3 а31 …. а33 b3      b1 a12 a13 a11 b1 a13 a11 a12 b1 b1 a12 a13 a11 b1 a13 a11 a12 b1 b2 a22 a23 b2 a22 a23  a21 b2 a23 a21 b2 a23 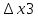 a21 a22 b2 a21 a22 b2b3 …. a33 a31 b3 a33 a31 …. b3 x1=  x2= x2=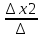 Метод обратной матрицы используется при решении систем линейных алгебраических уравнений, если число неизвестных равно числу уравнений. Заданасистема  a11x1 + a12x2 + …. + a1nxn= b1 …… ………. …….. ……… ….. an1x1 + an2x2 + …. + annxn = bn A*X=B       a11 a12 …. a1n b1 x1 A= a21 a22 … a2n B= b2 x= x2 a31 a32 … annbnxn Умножаем обе части матричного уравнения слева на   *А*Х= *А*Х= *B *B *A=E, то E*X= *A=E, то E*X= *B или X= *B или X= *B *B Далее находится обратная матрица  и умножается на столбец свободных членов В. и умножается на столбец свободных членов В.Комплексным числом называется выражение вида Z= a+bi, где a,b- произвольные действительные числа; i- мнимая единица 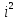 =-1 =-1 Действительное число a называется действительной частью комплексного числа z=a+bi и обозначается a=Rez Действительное число b называется мнимой частью числа z=a+bi обозначается b= Imz Алгебраическая форма комплексного числа В алгебраической форме комплексное число записывают в виде a+bi, где a и b- вещественные числа. Два комплексных числа a+bi и c+di равны тогда и только тогда, когда a=c, b=d. Тригонометрическая форма комплексного числа Тригонометрической формой комплексного числа z=x+iy, не равно нулю, называется запись z=rcos ȹ+ Isin ȹ) , где r= 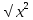 + +  - модуль комплексного числа z. - модуль комплексного числа z.Показательная форма комплексного числа Показательной формой комплексного числа называется выражение z= 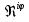 , где r= , где r= = =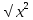 + + - модуль комплексного числа, - модуль комплексного числа, 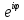 -расширение экспоненты на случай, когда показатель степени является комплексным числом. -расширение экспоненты на случай, когда показатель степени является комплексным числом.Пусть комплексное число z записано в тригонометрической форме z=(cos 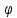 + I i sin + I i sin 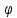 )= )= 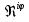 . Используем формулу Эйлера, получаем . Используем формулу Эйлера, получаем Z= r(cos 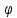 + sin + sin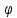 )= )=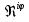 Сложение: Суммой комплексных чисел z1=a1+b1 и z2=a2+b2 называется комплексное число z, действительная часть которого равна суме действительных частей z1 и z2, а мнимая часть- сумме мнимых частей чисел z1 и z2, то есть z=(a1+a2) + (b1+b2)i. Вычитание: Вычесть из комплексного числа z1 комплексное число z2 значит найти такое комплексное число z, что z+z2=z1. Умножение: Произведением комплексных чисел z1=a1+b1i и z2=a2+b2i называется комплексное число z, определяемое равенством: z=(a1*a2-b1*b2)+ (a1*b2+a2*b1)i Деление: Разделить комплексное число z1 на комплексное число z2,значит найти такое комплексное число z, что z*z2=z1 . Теорема: Частное комплексных чисел существует и единственно, если z2  0+0i 0+0iВозведение в целую положительную степень А) Степени мнимой единицы Пользуясь равенством 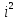 =-1, чтобы возвести число I в целую положительную степень, надо показатель степени разделить на 4 и возвести I в степень, показатель которой равен остатку от деления. =-1, чтобы возвести число I в целую положительную степень, надо показатель степени разделить на 4 и возвести I в степень, показатель которой равен остатку от деления.Б) Возведение комплексного числа в целую положительную степень Возводится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей. Умножение: При умножении двух комплексных чисел в тригонометрической или показательной формах их модули перемножаются, а аргументы складываются:  = =  * *  , arg( z1*z2)= arg z1 + arg z2 , arg( z1*z2)= arg z1 + arg z2Z1*z2=p1 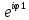 * p * p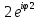 =p1p2* =p1p2* 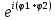 Z1*z2=p1p2( cos(  + +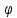 2) + isin( 2) + isin( 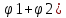 ) )Деление: При делении двух комплексных чисел заданных в тригонометрической или показательной формах их модули делятся, а аргументы вычитаются:  =arg =arg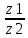 =arg z1-arg z2 =arg z1-arg z2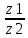 = =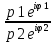 = =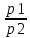 * *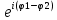 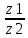 = =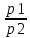 (cos ( (cos (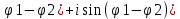 Возведение в степень: Для возведения комплексного числа в целую положительную степень n применяют формулу Муавра:  = =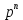 (cos n (cos n Извлечение корня порядка n Для извлечения корня используем формулу:  = =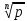 ( cos ( cos  . Где k=0,1.., n-1 . Где k=0,1.., n-1Построить вектор- геометрическое изображение комплексного числа. Отметить на чертеже острый угол от вектора до ближайшей к нему части оси ОХ и угол- от положительной части оси ОХ до вектора. Вычислить модуль 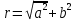 . Вычислить tg . Вычислить tg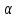 = = и определить по его значению острый угол. и определить по его значению острый угол. По найденному значению и чертежу определить аргумент. Подставить найденные значения модуля и аргумента в запись тригонометрической и показательной форм. Перевод комплексного числа из тригонометрической формы в алгебраическую: Вычислить косинус и синус. Раскрыть скобки Перевод комплексного числа из тригонометрической формы в показательную и наоборот: В обеих формах комплексное число определяется модулем и аргументом. Переписать в нужной форме Перевод из комплексного числа показательной формы в алгебраическую: Выполнить требуемый перевод через тригонометрическую форму. Раскрытие неопределенности Бесконечно малое- числовая функция или последовательность, которая стремится к нулю. Бесконечно большое- числовая функция или последовательность, которая стремится к бесконечности определенного знака Формула первого замечательного предела: 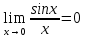 Следствия первого замечательного предела:  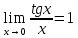 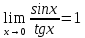  Второй замечательный предел 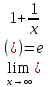 Следствие второго замечательного предела:    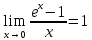 Производной функцией F (x) в точке x называется предел отношения приращения функции в точке x. Формулы дифференцирования: С’ =0= Const 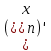 = =  ( 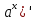 = = 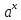 * lna * lna(  = =  (  = =  (ln x)’ =  ( 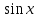 )’ = )’ = 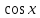 (  ’ = - ’ = -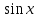 ( 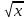 )’ = )’ =  ( 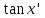 ) = ) = ( 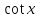 )’ =- )’ =-  (arcsin x)’ = 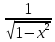 (arccos x)’ = - 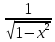 (arctg x)’ = 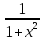 (arcctg x)’ = - 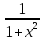 Правила дифференцирования: Константу можно выносить за знак производной: (c*u (x))’ = c*u’ (x) Производная суммы равна сумме производных: (u (x)  (x))’ = u’ (x) (x))’ = u’ (x)  𝑣’ (x) 𝑣’ (x)Производная произведения равна сумме произведений производной первого слагаемого на второе и первого слагаемого на производную второго: (u (x) * 𝑣 (x))’ = u’ (x)𝑣 (x) + u (x) 𝑣’ (x) Производная частного находится по формуле:  = = 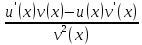 , 𝑣 (x) , 𝑣 (x) 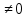 Пусть задана сложная функция y= f 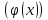 , то тогда производная этой сложной функции находится по правилу: , то тогда производная этой сложной функции находится по правилу:y’=f’ ( 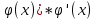 сначала находится производная внешней функции, аргумент не изменяется, а затем находится производная от ее аргумента. Если функция f’(x) дифференцируема, то ее производная называется производной второго порядка и обозначается: y”; f”(x);  ; y”=(y’)’ ; y”=(y’)’Производная от производной второго порядка ,если она существует называется производной третьего порядка и обозначается: y”’; f”(x);  ; y”’=(y”)’ ; y”’=(y”)’Производной n-ного порядка называется производная от производной n-1 –ого порядка 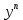 = ( = (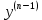 )’ )’Функция Fназывается первообразной для функции fна заданном промежутке, если для всех х из этого промежутка F’(X) = f(x) Неопределенным интегралом от непрерывной на интервале (a;b) функции f(x) называют совокупность ее первообразных функций 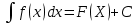 Где f(x)- подинтегральная функция; f(x)dx- подинтегральное выражение (дифференциал); С- постоянная интегрирования Основные свойства интеграла: Вынос константы за знак интеграла: 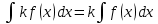 Интеграл разности/суммы функций равен разности/сумме интегралов от этих функций: 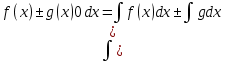 Производная интеграла равна выражению, стоящему под знаком интеграла: 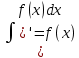 Интеграл от производной функции равен сумме функций плюс постоянная:  Интеграл дифференцирования функции равен самой функции плюс постоянная интегрирования: 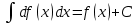 Табличные формулы неопределенных интегралов 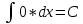   +C,n +C,n ,x ,x  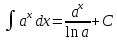  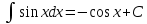 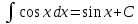 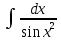 = - ctgx+C = - ctgx+C = tgx+ C = tgx+ C = arcsin = arcsin  +C , +C ,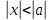  = = 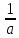 arctg arctg + C + C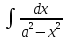 = = 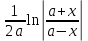 +C, +C,  Сущность этого метода заключается в том, что путем введения новой переменной интегрирования удается свести заданный интеграл к новому интегралу, то есть берется методом непосредственного интегрирования. 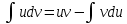 Определенным интегралом от функции f(x) на отрезке (a;b) называется предел (если о существует) интегральной суммы для функции f(x) на отрезке (a;b), не зависящий от способа разбиения отрезка (a;b) и выбора точек С, найденный при условии, что длины элементарных отрезков (включая и максимальная  стремятся к нулю. стремятся к нулю. Свойства определенного интеграла 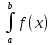 dx= - dx= -    , k- любое число , k- любое число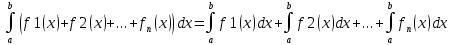 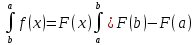 Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных и производные различных порядков этой функции. F’(X)= f(x),  Общим решением дифференциального уравнения первого порядка называется семейство функций вида y=  , зависящее от произвольной постоянной С, каждая из которых является решением данного дифференциального уравнения при любом допустимом значении произвольной постоянной С. Таким образом, дференциальное уравнение имеет бесчисленное множество решений. , зависящее от произвольной постоянной С, каждая из которых является решением данного дифференциального уравнения при любом допустимом значении произвольной постоянной С. Таким образом, дференциальное уравнение имеет бесчисленное множество решений.Частным решением дифференциального уравнения называется решение, получаемое из формулы общего решения при конкретном значении произвольной постоянной С, включая  . .Дифференциальное уравнение y’=f(x.y) называется уравнение с разделяющимися переменными, если его можно записать в виде: Y’= 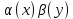 Можно представить также в виде: y’- 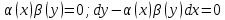 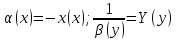 Получаем: X(x)dx+Y(y)dy=0;  После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными. Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, и частное решение. Сумма членов бесконечной числовой последовательности u1.u2,…, 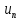 ,… называется числовым рядом. ,… называется числовым рядом.u1+u2+…+ 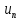 +…= +…= Пусть задан положительный числовой ряд 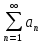 то то Если ряд сходится, то предел его общего члена равен нулю:  =0 =0Если предел общего члена ряда не равен нулю, то ряд расходится:  0 0Следствие: Если  = =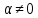 то ряд 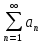 расходится расходится Признак сравнения: Пусть даны ряды  и и  . Если ряд с большими членами сходятся, то сходятся и ряд с меньшими членами. Если же ряд с меньшими членами расходится, то расходится и ряд с большими членами . Если ряд с большими членами сходятся, то сходятся и ряд с меньшими членами. Если же ряд с меньшими членами расходится, то расходится и ряд с большими членамиРассмотрим положительный числовой ряд 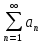 . Если существует конечный предел . Если существует конечный предел  =I, то при I =I, то при I ряд сходится, при I ряд сходится, при I ряд расходится. ряд расходится. При k=1 вопрос о сходимости ряда остается нерешенным и нужно подобрать другой признак для исследования данного ряда. Ряд называется знакочередующимся, если любые два его соседних члена имеют разные знаки, то есть 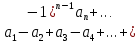 = = Для получения формулы прямоугольников интервал интегрирования (a;b) разбивается на n подынтегралов равной длины точками:  =a, =a,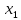 , ,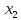 ,…, ,…,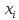 , , ,.., ,..,  =b так, что =b так, что  - - 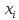 =h= =h=  , i=1,2,…,n , i=1,2,…,nНа этих подынтервалах строятся прямоугольники, высота их определяется значением функции f(x) в какой либо точке подынтервала. Если f(  определяется для левой границы каждого подынтервала, то формула прямоугольников имеет вид: определяется для левой границы каждого подынтервала, то формула прямоугольников имеет вид: = = и называется формулой левых прямоугольников. и называется формулой левых прямоугольников.Если f(  определяется для правой границы каждого подынтеграла, то определяется для правой границы каждого подынтеграла, то  = = и называется формулой правых прямоугольников. и называется формулой правых прямоугольников.Если функция монотонна на отрезке (a;b), то в одном случае получается значение интеграла I с недостатком  , а в другом- с избытком , а в другом- с избытком  . Более точное значение I получают при усреднении величин: . Более точное значение I получают при усреднении величин:I= 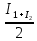 Если f(  определяется для середины каждого подынтеграла, то формула прямоугольников имеет вид: определяется для середины каждого подынтеграла, то формула прямоугольников имеет вид: и называется формулой средних прямоугольников. и называется формулой средних прямоугольников.Формула метода трапеций 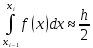  Интегрируемый отрезок (a;b) делится на равные отрезки длиной h. Каждый отрезок функции аппроксимируется параболой. Парабола проходит через три точки: узлы интегрирования  , ,  и середину отрезка и середину отрезка  F(x)=  Площадь параболы на отрезке (   Тогда интеграл функции на отрезке (a;b) 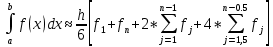 Численное решение заключается в вычислении функции y(x) и ее производных в некоторых заданных точках 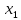 , , 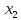 ,…, ,…, , лежащих на определенном отрезке , лежащих на определенном отрезке В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения. Угловой коэффициент касательной к интегральной кривой в точке 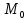 ( ( , , ) равен ) равен 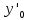 =f( =f( , , ). ). Найдем ординату  касательной, соответствующей абсциссе касательной, соответствующей абсциссе 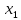 = = +h +hУравнение касательной к кривой в точке 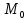 имеет вид y- имеет вид y- = =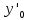 (x- (x- ) или y= ) или y= + +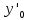 (x- (x- ), откуда ), откуда  = = +hf( +hf( , , ) )Множество совокупность определенных различаемых объектов таких ,что для любого объекта можно установить, принадлежит этот объект данному множеству или нет. Объекты, составляющие множество, называются его элементами. Множества обозначают заглавными буквами, а его элементы- соответствующими малыми. Первый способ: простое перечисление элементов множества.  Второй способ: задать множество с помощью так называемого характеристического условия P(x)  Третий способ: задать множество с помощью так называемой порождающей процедуры. Порождающая процедура описывает, как получить элементы множества из уже известных элементов или неких иных объектов. Равными называют два множества A и B, состоящие из одинаковых элементов: A=B Множество, не содержащее ни одного элемента, называется пустым и обозначается символом  49)Свойства множеств относительно операции объединения: Коммутативность A  B= B B= B Ассоциативность (A  ) ) C= A C= A Дистрибутивность A 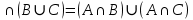 Идемпотентность  Закон де Моргана 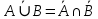 Операции с множеством A  Операции с множеством A 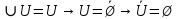 Законы поглощения A  A  Свойства множеств относительно операции перечисления Коммутативность  Ассоциативность (A 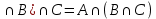 Дистрибутивность 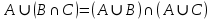 Идемпотентность 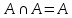 Закон де Моргана  Операции с множеством 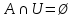 Операции с множеством 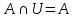 Законы поглощения   50) |
