Исследовательская работа по математике. Исследовательскаяработа по математике. Матричная алгебра на практике
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
|
Воронежская область, Петропавловский район, с. Старая Криуша, МКОУ Старокриушанская СОШ «Матричная алгебра на практике» исследовательская работа. Зайцева Валерия Сергеевна, ученица 11 класса, Научный руководитель Бургонова Ирина Ивановна, учитель математики 2021 год Оглавление. Введение. 3 Основная часть. 4 1.1.Теоретические аспекты матрицы. 4 1.1.1. История развития и применение матриц. 4 1.1.2. Основные сведения о матрицах. 6 1.1.3. Виды матриц. 6 1.2. Действия над матрицами. 7 1.2.1. Сложение матриц. 7 1.2.2. Умножение матрицы на число. 8 1.2.3. Умножение матриц. 8 1.2.4. Транспонирование матрицы. 9 1.3. Определители. Основные понятия. 10 1.4. Обратная матрица. 13 II. Практическая часть. 16 2.1. Метод элементарных преобразований. 16 2.2. Решение матричных уравнений. 17 2.3. Метод Гаусса. 20 III. Применение матриц в повседневной жизни. 23 Заключение. 24 Список литературы. 25 Введение Термин «матрица» имеет много значений. Например, в математике матрицей называется таблица, в которую записаны значения числовых величин. В электронике «матрицей» называют электронную схему, состоящую из отдельных элементов (транзисторов, диодов и т. д.). В технике матрицами принято называть также микросхемы. Матрицы применяются в повседневной жизни и используются во всех отраслях деятельности. При решении различных практических задач в математике, биологии, физике, технике, химии, экономике, маркетинге, психологии и других областях науки используют матрицы. В повседневной жизни матрицами являются карты, таблицы, графики. Цель: изучить основные аспекты матричной алгебры. Задачи: Изучить все возможные операции над матрицами. Научиться с помощью матричной алгебры решать системы линейных уравнений методом Гаусса. Узнать, где применяются матрицы в жизни человека. Гипотеза: полученные знания в ходе выполнения исследовательской работы пригодятся в дальнейшем обучении и повседневной жизни. Актуальность: Сегодня любому квалифицированному экономисту, финансисту, логисту, статисту просто необходима мощная математическая база. Для них одним из главных предметов в высшей математике является линейная алгебра, а именно, - матричная алгебра. Именно она является наиболее компактной и удобной для решения многих поставленных задач. Матричные методы все чаще применяются на практике: различные виды статистических расчётов, сокращение документооборота, организация внутри производства хозяйственных расчётов и экономико-математического анализа. Поэтому, выполнив свою работу, я получу полезные знания, которые, уверенна, пригодятся мне в будущем. Объект исследования: матрицы Предмет исследования: способы решения линейных систем уравнений. Методы исследования: наблюдение, анализ, синтез, сравнение. 1.Основная часть 1.1. Теоретические аспекты матрицы 1.1.1. История развития и применение матриц
В конце XVII века получило развитие теория определителей и тогда швейцарский математик Габриэль Крамер (1704-1752) приступил к разработке своей теории. В 1751 году он опубликовал «правило Крамера» и параллельно в это же время был опубликован «метод Гаусса». Эти две публикации раскрывали метод решения «систем линейных алгебраических уравнений», но для «правила Крамера» используется ненулевой определитель матрицы системы, а для «метода Гаусса» - последовательное исключение неизвестных. Теория матриц начала активное развитие в середине XIX века. В это время уже были формулированы правила сложения и умножения матриц. Результаты теории матриц разработаны и отражены в работах ученых: ирландский математик и физик Уильям Гамильтон (1805-1865), английский математик Артур Кэли (1821-1895), немецкие математики Карл Вейерштрасс (1815-1897) и Фердинанд Георг Фробениус (1849-1917), французский математик Мари Энмон Камиль Жордан (1838-1922) и ввел термин «матрица» Джеймс Сильвестр (1814-1897) в 1850г. В 1858году А.Кэли опубликовал «Мемуар по теории матриц», в котором дается первое абстрактное определение матрицы. У.Гамильтон и А.Кэли разработали теорию матриц: «любая квадратная матрица удовлетворяет своему характеристическому уравнению». В 1878 году Ф.Г.Фробениус опубликовал работу «О линейных подстановках и алгебраических уравнениях», в которой доказывает результаты канонических матрицах. Он также доказал общую теорему матриц: «матрица удовлетворяет своему характеристическому уравнению». К.Вейерштрасс в своих лекциях использовал аксиоматическое определение определителя, а в 1903году после его смерти было опубликована статья «О теории детерминантов». Мари Энмон Камиль Жордан ввел нормальную (каноническую) форму матриц, которая имеет вид блочно-диагональной матрицы, по диагонали располагаются жордановы клетки. Матрицы широко применяются в математике, физике, информатике, химии, биологии, экономике, технике, статистике и т.д. Они играют огромную роль в каждой сфере и значение их велико. В математике «матрица» означает систему элементов в прямоугольной таблице, в программировании - двумерный массив, в электронике – набор проводников, в фотографии – интегральная микросхема. Матрица встречается везде даже в таких таблицах как: таблица умножения, файл bmp с матрицей цветов пикселей, турнирная таблица на футбольном поле, таблица содержания в пище белков, жиров и углеводов. 1.1.2.Основные сведения о матрицах Матрица — это прямоугольная таблица, образованная из элементов некото- рого множества и состоящая из m строк и n столбцов. Обозначения матрицы: 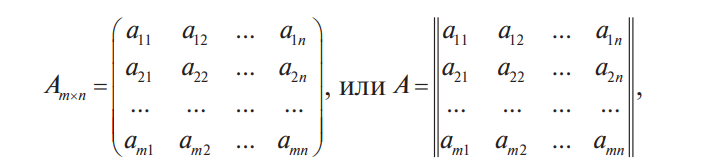 Если m = n, то матрица называется квадратной, а число m = n — ее порядком: 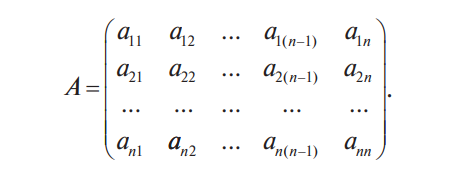 (1.1) (1.1) Главной диагональю матрицы (1.1) называется диагональ а11, а22, а33, …, аnn Побочной диагональю матрицы (1.1) называется диагональ a1n, a2(n-1), …, an1. Матрицы A и B одного размера называются равными, если они совпадают поэлементно, т. е. для любых . 1.1.3. Виды матриц 1. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной. Например,  2. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной и обозначается буквой Е или I. Например,  3. Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О. 4. Квадратная матрица называется верхней треугольной, если все элементы, расположенные ниже главной диагонали, равны нулю. Например, 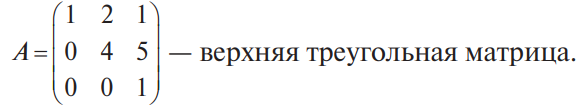 5. Квадратная матрица называется нижней треугольной, если все элементы, расположенные выше главной диагонали, равны нулю. Например, 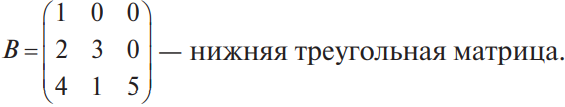 6. Матрица, содержащая один столбец или одну строку, называется вектором (вектор-столбцом или вектор-строкой соответственно). Например, 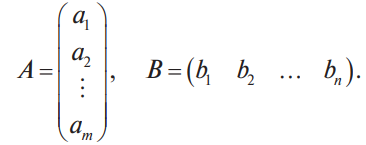 Матрица размера 1x1, состоящая из одного числа, отождествляется с этим числом. Например, 1.2. Действия над матрицами 1.2.1. Сложение матриц Суммой двух матриц Обозначение: C = A + B. Пример. Найти сумму матриц 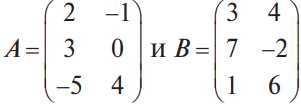 . .Решение: 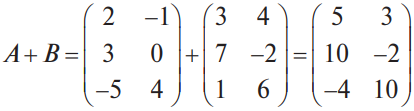 . .Свойства сложения матриц. Переместительное свойство: A + B = B + A Сочетательное свойство: (A + B) + C = A + (B + C). 1.2.2. Умножение матриц на число Произведением матрицы Пример. Умножить матрицу Решение: Свойства умножения матрицы на число. 1. Сочетательное свойство относительно числового сомножителя: 2. Распределительное свойство относительно суммы матриц: 3. Распределительное свойство относительно суммы чисел: 1.2.3. Умножение матриц Произведением матрицы 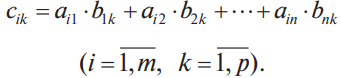 Обозначение: C = А* В Операция умножения двух матриц определяется только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы. Пример. Найти произведение матриц А и В, если Решение: 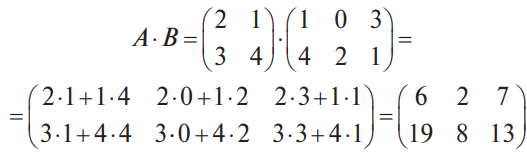 Свойства произведения матриц. 1. Перестановочное свойство в общем случае не выполняется: 2. Сочетательное свойство: 3. Распределительное свойство относительно суммы матриц: 4. Если А — квадратная матрица, а Е — единичная матрица того же порядка, что и А, то ЕА = АЕ = А. Замечание : Если АВ = ВА то матрицы А и В называют перестановочными или коммутирующими.  1.2.4. Транспонирование матриц 1.2.4. Транспонирование матрицМатрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначение: Пример. Транспонировать матрицу . . Решение: . Свойства операции транспонирования 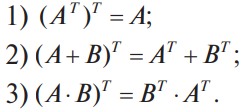 Квадратная матрица А называется симметрической, если она совпадает со своей транспонированной, то есть Квадратная матрица А называется кососимметрической, если совпадает со своей транспонированной, умноженной на число (–1), то есть 1.3. Определители. Основные понятия. Для квадратной матрицы А порядка n введем числовую характеристику, называемую определителем или детерминантом. Обозначение: 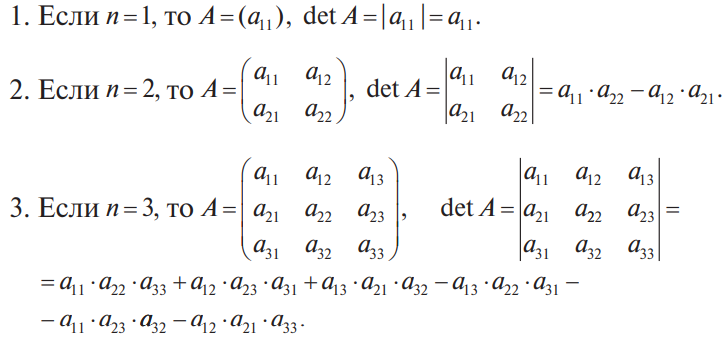 Это правило вычисления определителя третьего порядка называется правилом Саррюса или правилом треугольников. Пример. Найти определитель матрицы: 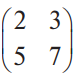 . Решение: . Решение: 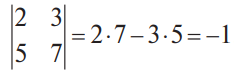 Свойства определителей. Перечисленные ниже свойства справедливы для определителей любого порядка. 1. При транспонировании матрицы ее определитель не изменяется. Например, 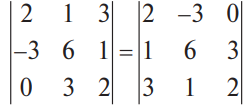 . .Назовем строки и столбцы рядами определителя. При перестановке двух параллельных рядов определитель меняет знак. Например, 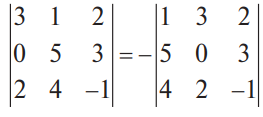 . .Определитель, имеющий два одинаковых ряда, равен нулю. Например, 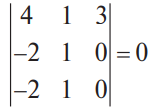 . .5.При умножении какого-либо ряда определителя на любое число определитель умножается на это число. Например, 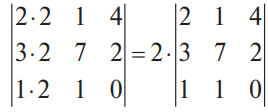 6. Если все элементы какого-либо ряда равны нулю, то определитель равен нулю. Например, 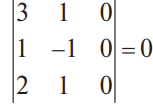 . .7. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей. Например, 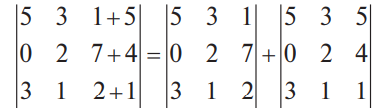 . .8. Если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на некоторое число, то определитель не изменится. Например, 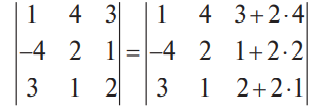 Минором элемента Алгебраическим дополнением элемента 9. Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения, то есть, например, разложение определителя по i‑й строке имеет вид: 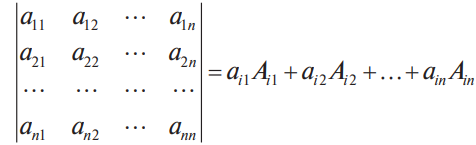 Пример. Вычислить определитель: 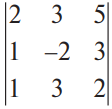 Решение. Разложим определитель по первой строке: 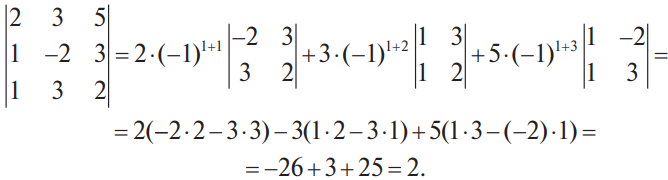 10. Сумма произведений элементов какого-либо ряда определителя на алгебраи-ческие дополнения соответствующих элементов параллельного ряда равна нулю. Например, 11. Определитель произведения двух квадратных матриц равен произведению их определителей 12. Определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали этой матрицы. Н 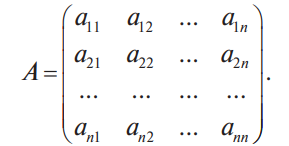 апример, апример,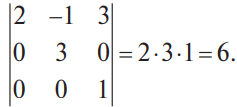 13. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали. Например, 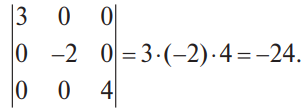 Отсюда следует, что определитель единичной матрицы любого порядка равен единице. 1.4. Обратная матрица. Пусть А — квадратная матрица n-го порядка: Квадратная матрица А называется невырожденной (неособенной), если определитель матрицы А не равен нулю, т. е. Если матрица А невырожденная, то существует и притом единственная матрица A-1 , такая, что где Е — единичная матрица. Методы вычислений обратной матрицы. 1. Метод присоединенной матрицы Присоединенная матрица — это матрица, составленная из алгебраических дополнений данной матрицы и транспонированная. Обозначение: 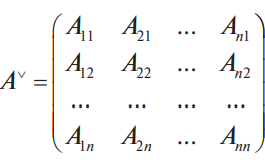 . .Справедливо следующее равенство: Отсюда следует, что если матрица А невырожденная, то Составим присоединенную матрицу: 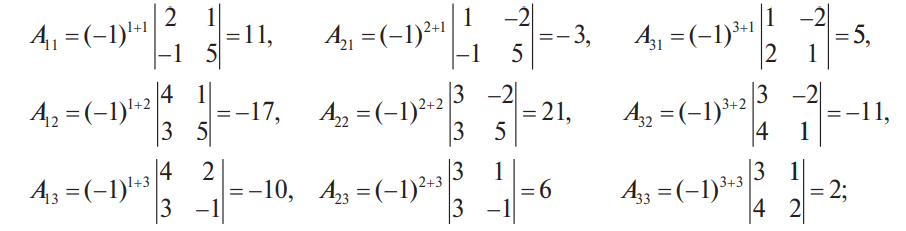 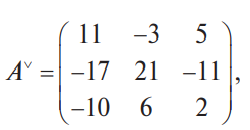 тогда тогда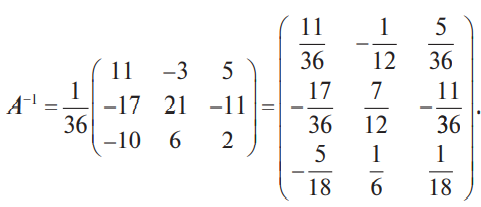 Итак, 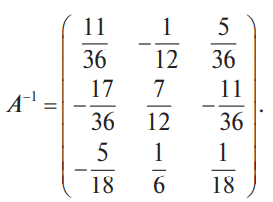 Проверка: 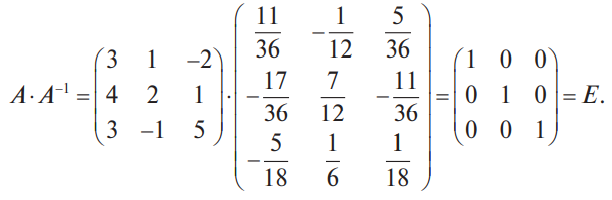 Свойства обратной матрицы: 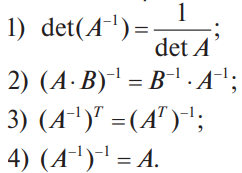 II.Практическая часть. 2.1. Метод элементраных преобразований Элементарными преобразованиями матрицы являются: 1) перестановка строк (столбцов); 2) умножение строки (столбца) на число, отличное от нуля; 3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число. Для квадратной матрицы А n-го порядка построим прямоугольную матрицу Далее, используя элементарные преобразования над строками, приводим матрицу Тогда Пример. Найти 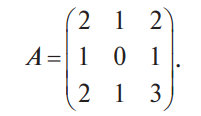 Решение. Образуем матрицу 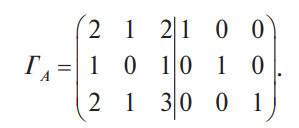 С помощью элементарных преобразований приведем матрицу к виду (E | В ). 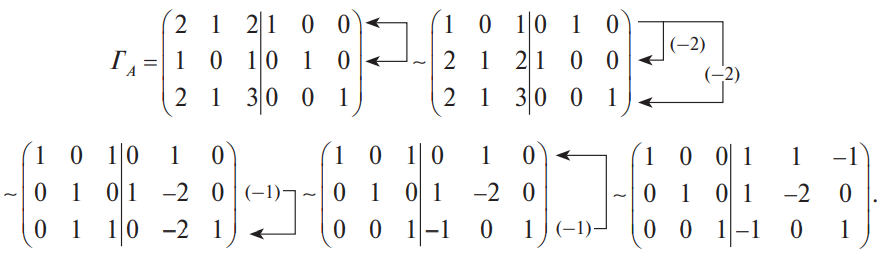 Итак, 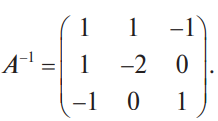 Проверка: 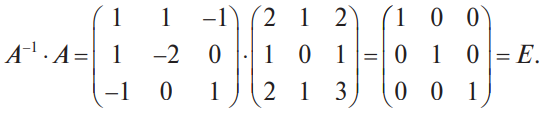 2.2. Матричные уравнения Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например, ax=b, где x - неизвестное. А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы - это матрицы. Итак, матричным уравнением называется уравнение вида A ⋅ X = B или X ⋅ A = B, где A и B - известные матрицы, X - неизвестная матрица, которую требуется найти. Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B, обе его части следует умножить на обратную к A матрицу По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: Как решить матричное уравнение во втором случае? Если дано уравнение X ⋅ A = B,то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A, и умножать матрицу B на неё справа: Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения A ⋅ X ⋅ B = C, является Пример 1. Решить матричное уравнение Решение. Данное уравнение имеет вид A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде Сначала найдём определитель матрицы A: Найдём алгебраические дополнения матрицы A: Составим матрицу алгебраических дополнений: Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A: Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A: Наконец, находим неизвестную матрицу: 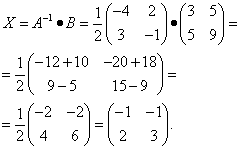 Пример 2. Решить матричное уравнение Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде Сначала найдём определитель матрицы A: Найдём алгебраические дополнения матрицы A: Составим матрицу алгебраических дополнений: Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A: Находим матрицу, обратную матрице A: Находим неизвестную матрицу: 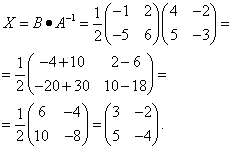 2.3. Метод Гаусса. Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Решить методом Гаусса систему линейных уравнений 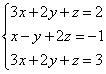 Для упрощения внешнего вида решения составим расширенную матрицу системы: 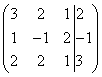 В этой матрице слева до вертикальной черты расположены коэффициенты при неизвестных, а справа после вертикальной черты - свободные члены. Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы. Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения: 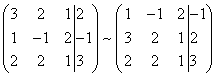 С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую строку, умноженную на Это возможно, так как Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус. В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменную x: 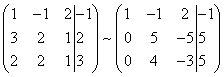 Для упрощения второй строки полученной системы умножим её на 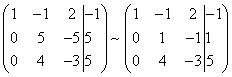 Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую строку, умноженную на Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус. В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений: 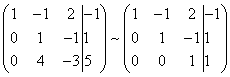 Мы получили эквивалентную данной трапециевидную систему линейных уравнений: 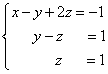 Если число уравнений и переменных больше, чем в нашем примере, то процесс последовательного исключения переменных продолжается до тех пор, пока матрица системы не станет трапециевидной, как в нашем демо-примере. Решение найдём "с конца" - обратный ход. Для этого из последнего уравнения определим z: Подставив это значение в предшествующее уравнение, найдём y: Из первого уравнения найдём x: Ответ: решение данной системы уравнений - 3.Применение матриц в повседневной жизни Матрицы проникли почти во все отрасли человеческой деятельности. Они используются в математике, в физике, в технике, в экономике, в теории управления, статистики, других областей науки и знаний. Для решения различных практических задач используется всевозможное программное обеспечение, например, Microsoft Excel, MathСad, Maple, которые позволяют манипулировать целыми массивами без выполнения вычислений вручную. Рассмотрим применения матриц в повседневной жизни. Пусть частный предприниматель имеет жилое (44м2) и офисное помещения (71м2). Каждый месяц ему необходимо оплачивать коммунальные услуги, вычислим значения платежей по каждому виду и общую сумму. Тарифы по предоставляемым услугам жилищной компанией для жилых помещений: холодное водоснабжение составляет 16,2 руб. за 1м3, горячее водоснабжение -117 руб., электроэнергия - 2,81 руб. за 1кВт.ч., отопление - 1389 руб. за 1Гкал. Для офисных помещений с владельцев взимается оплата в размере двойного тарифа от жилого фонда. Потребляемые ресурсы по данным помещениям представлены в таблице 1.
Данные по потреблению ресурсов (табл.1) внесем в матрицу. Тарифы по услугам запишем в матрицу, вначале идут значения, которые соответствуют жилому помещению, затем – офисному. Вычислим общую сумму расходов по услугам в месяц за оба помещения: каждый элемент получившейся матрицы – это значение, которое соответствует плате за определенную услугу потребления. Общая сумма коммунальных платежей находится по формуле: S=16,2*(х11+х12)+ 117*(х21+х22)+2,81*(х31+х32)+1389*(х41+х42) где х11, х12, х21, х22, х31, х32, х41, х42 – элементы матрицы. Чтобы предприниматель мог ежемесячно знать сколько ему нужно оплатить в общем, он вводит только новые значения по потреблению в матрицу, в случае изменения тарифов также легко вносятся новые значения в матрицу. Предложенный способ позволяет предпринимателю быстро и безошибочно рассчитывать сумму ежемесячных коммунальных платежей. При решении практических задач матрицы являются хорошими помощниками, так же они используются в решении экономических задач в сферы планирования и управления с помощью линейного программирования. Заключение В ходе выполнения исследовательской работы я рассмотрела все аспекты матричной алгебры: историю возникновения матриц и ее изучения, определение матрицы, форму записи, основные свойства и виды матриц. Рассмотрела операции, которые можно производить с матрицами, свойства матриц. Применила данные знания при решении не только матричных, но и линейных уравнений (метод Гаусса). Поставленной цели и задач в ходе выполнения работы я добилась. Считаю, что гипотеза, выдвинутая мною в начале работы, полностью подтвердилась: полученные знания по данной теме пригодятся не только в дальнейшем обучении в ВУЗе, но и в повседневной жизни. Список литературы. 1.Бурмистрова Е.Б.: Линейная алгебра, дифференциальное исчисление функций одной переменной. - М.: Экономика, 2010 2. Гантмахер Ф.Р.: Теория матриц. - М.: Физматлит, 2004 3. "Матрица" как философия / ред. О. Турухина. - М.: Екатеринбург: У-Фактория, 2014. - 384 c. 4. Беллман, Р. Введение в теорию матриц / Р. Беллман. - М.: [не указано], 2016. - 646 c. 5.Чью, Дж. Аналитическая теория S-матрицы / Дж. Чью. - М.: [не указано], 2016. - 631 c. |

