матрицы. Матрицы. Матрицы. Основные понятия. Матрицей называется прямоугольная таблица чисел. Пример 13
 Скачать 144.4 Kb.
|
|
Матрицы. Основные понятия. Матрицей называется прямоугольная таблица чисел. Пример 13. 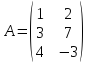 ,  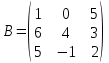,  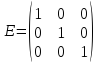,  .В общем случае матрица может содержать 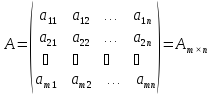 строк и  столбцов .Числа  называются элементами матрицы, где  - указывает номер строки,  - указывает номер столбца.Элементы  образуют главную диагональ матрицы. Если число строк равно числу столбцов, то матрица называется квадратной. Квадратная матрица размеров  называется матрицей – го порядка.Матрицы называются равными, если у них равны элементы, стоящие на соответствующих местах, т. е.  тогда и только тогда, когда  , для всех  ,  .Квадратная матрица, у которой все элементы, кроме главной диагонали равны 0, называется диагональной. Пример 14. 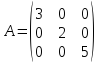 .Если все элементы матрицы равны нулю, то матрица называется нулевой. Пример 15. 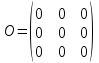 .Диагональная матрица, у которой каждый элемент диагонали равен 1, называется единичной. Пример 16. 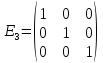 ,  .Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от диагонали, равны нулю. Пример 17. 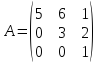 ,  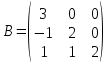.Матрица, содержащая одну строку (столбец), называется вектором(вектор-строкой, вектор-столбцом). Пример 18. 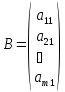 ,  .Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной  .Пример 19. 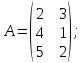  ;Очевидно, что  .Действия над матрицами. Матрицы одинаковых размерностей можно складывать и вычитать. Если  ,  , то  , причем 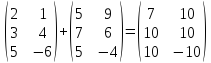, для всех  .Пример 20.  , .Умножение матрицы на число. Чтобы умножить матрицу на число, необходимо каждый ее элемент умножить на это число. Пример 21. Пусть  , тогда  . Матрица  называется противоположной к матрице .Умножение матриц. Умножение матриц  можно только в том случае, когда число столбцов матрицы равно числу строк матрицы  В этом случае справедливо соотношение  , причем элементы матрицы  равны  , ,  . Другими словами строки матрицы умножаются на столбцы матрицы Пример 22. Пусть 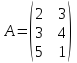 ,  . Тогда , .Видим, что в общем случае  . Если же выполняется условие  , то матрицы и  называются перестановочными друг с другом.Матрица называется ступенчатой, если для её элементов выполняются условия: под первым не нулевым элементом каждой строки находится 0; первый ненулевой элемент любой строки находится правее первого не нулевого элемента любой строки, расположенной выше. Пример 23. Следующая матрица является ступенчатой. 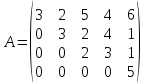 .Элементарные преобразования матриц. Элементарными преобразованиями матриц являются: Перестановка местами двух любых её строк (столбцов). Умножение элементов какой-нибудь строки (столбца) на некоторое не нулевое число. Прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число. Две матрицы  называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований Любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду. Определители. Определителемназывается квадратная числовая таблица, вычисляемая по определенным правилам. Пример 24. Если 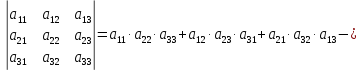 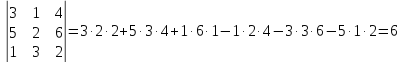, то  . Так  .Если  , то  .Так  .Если  , то  . Так .При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников. С плюсом берутся произведения элементов стоящих на главной диагонали и элементы, стоящие в вершинах следующих треугольников.  С минусом берутся произведения элементов, стоящих на второй диагонали и в вершинах следующих треугольников. В  торой метод заключается в том, что рядом с определителем справа записываются первый и второй столбцы и тогда с плюсом берутся произведения элементов, стоящих на главной диагонали и двух ей параллельных, с минусом – произведения элементов, стоящих на второй диагонали и двух ей параллельных. Вычисление определителей более высоких порядков осуществляется путем использования их свойств. Свойства определителей. Пусть дана квадратная матрица  Из элементов этой матрицы можно составить определитель, который называется детерминантом матрицы и обозначается Минором  некоторого элемента определителя называют определитель, который 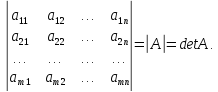получается вычеркиванием из него  строки и  столбца. Например ,  .Алгебраическим дополнениемэлемента 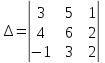определителя называют число  . Например ,  .Свойства определителей. 1. Определитель не изменится, если его строки заменить столбцами и наоборот, т. е.  .2. Определитель меняет знак при перестановке любых двух его строк (столбцов). 3. Определитель, имеющий две равные строки (столбца), равен 0. 4. Общий множитель строки (столбца) можно выносить за знак определителя, например  .5. Если элементы какой-нибудь строки (столбца) представимы в виде суммы двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, например 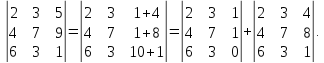 6. Определитель не изменится, если к какой-нибудь строке (столбцу) прибавить соответствующие элементы другой строки (столбца), умноженные на некоторое ненулевое число. 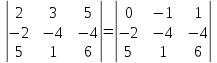 (I=I+II).7. Определитель треугольной матрицы равен произведению её диагональных элементов. 8. Определитель равен сумме произведений элементов какой-нибудь его строки (столбца) на их алгебраические дополнения. Например  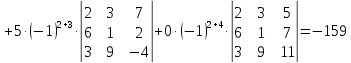 .Для вычисления определителя мы использовали разложение по второй строке, так как она содержит большее число нулевых элементов. 9. Сумма произведений элементов какой-нибудь строки (столбца) на соответствующее алгебраическое дополнение другой строки (столбца) равна 0. |