Детали машин. Механизм двухступенчатого двухцилиндрового компрессора
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
4.2.6 Построение эвольвентного зацепления открытой передачи Проводим вычисленные радиусы колеса и шестерни. На основных радиусах откладываем равноудаленные точки 1,2 ... 9 для шестерни и колеса (р1 = 11,79 и р2 = 17,69 мм соответственно), через которые проводим касательные. Через т.2 откладываем по касательной один отрезок с шагом р, через т. З два отрезка и т.д. Полученная плавная кривая является боковым профилем зубьев. Откладываем толщину зуба на вершинах и начальном диаметре колеса и через полученные точки строим симметричное изображение эвольвенты. Отложив угловой шаг, строим ещё два зуба для шестерни и колеса. Отрезок прямой, заключенный между точками N1 и N2, называют линией зацепления. Часть линии зацепления, отсекаемая от нее окружностями вершин, представляет геометрическое место действительных точек контакта парных профилей и называется активной линией зацепления Р1Р2 = ga. За время зацепления одной пары сопряженных профилей зубчатые колеса повернуться на некоторые углы φа1 и φа2. Угол поворота зубчатого колеса от момента входа его профиля в зацепление до момента выхода его из зацепления называют углом перекрытия. Дуги а1b1 и а2b2 стягивают углы перекрытия φа1 и φа2.  5 Синтез кулачкового механизма 5 Синтез кулачкового механизма5.1 Задачи синтеза кулачкового механизма Задачами синтеза кулачкового механизма являются: 1. Определение основных размеров механизма из условия ограниченности угла давления (Θi< Θдоп); 2. Построение профиля кулачка, обеспечивающего заданный закон движения толкателя. 5.2 Исходные данные Числа зубьев колес привода масляного насоса Za = 12, Zb= 18; Модуль зубчатых колёс Za и Zb m = 3 мм; Частота вращения колеса Za n1= 655 об/мин; Ход толкателя кулачкового механизма h = 18 мм; Внеосность толкателя е = 10 мм; Отношение ускорений а1/а2=1,8; Фазовые углы поворота кулачка: φn = φo =120°; φд.с.= 0; Допускаемый угол давления Θдоп = 25°; Масса толкателя mT = 0,60кг. 5.3 Расчёт передаточных функций выходного звена Аналог ускорения S", аналог скорости S' и перемещение S толкателя определяем аналитически для заданного законов движения. На фазе удаления и возвращения закон движения параболический:  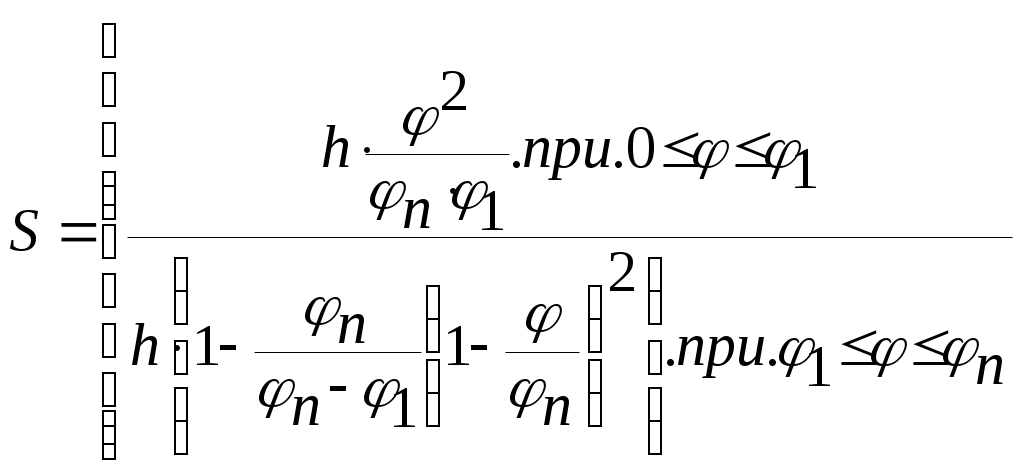 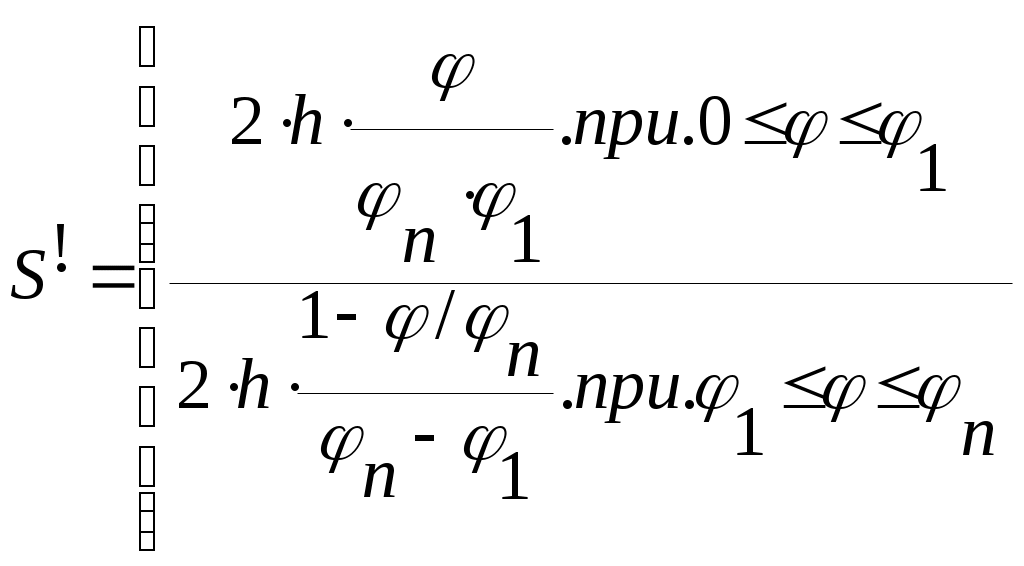 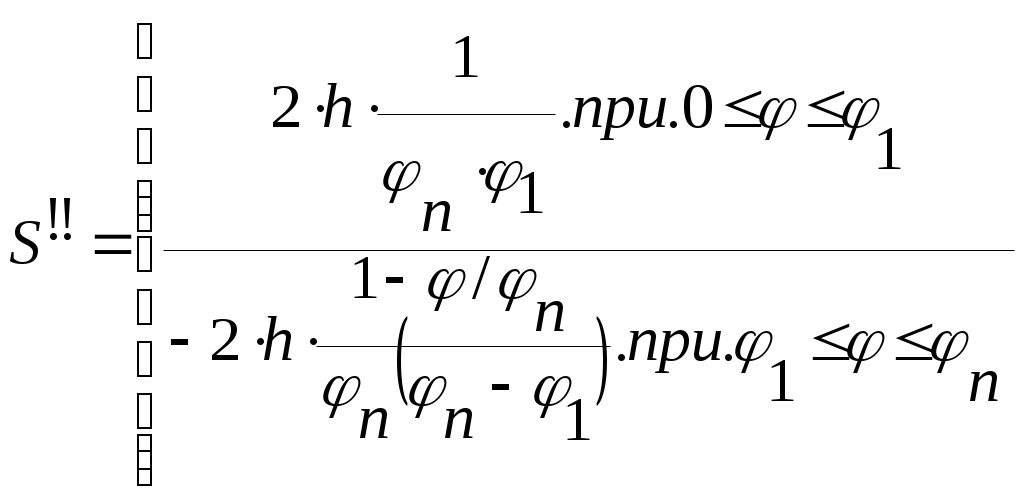 Из отношения ускорений определим φ1 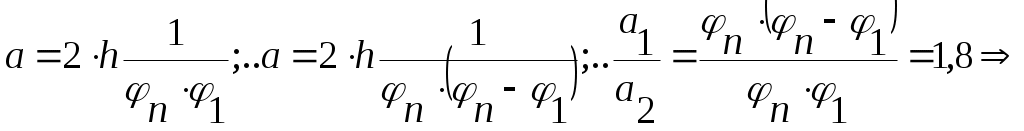 Для построения аналога скорости и ускорения необходимы только экстремальные значения 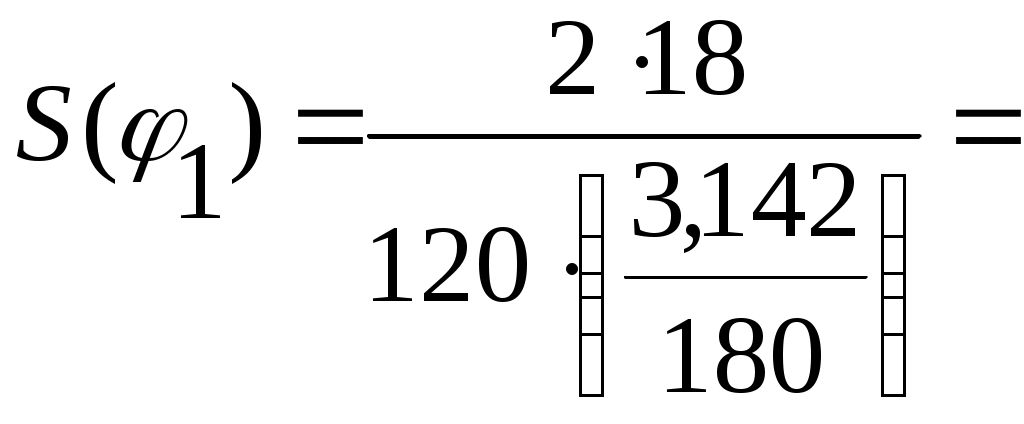 17.21 мм; 17.21 мм; 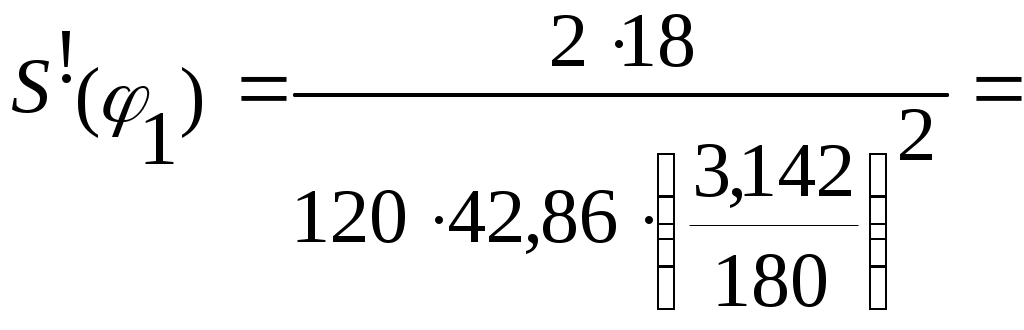 26,45 мм; 26,45 мм;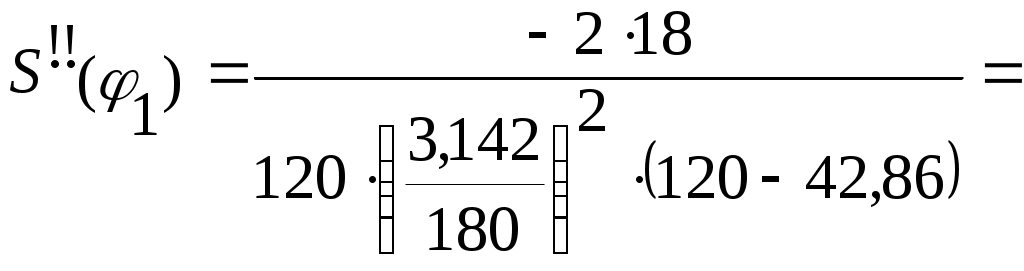 - 16,78 мм - 16,78 ммМасштабы построения выбираем равные μs = μs!= 0,25 Данные, полученные в результате вычислений, занесем в таблицу 5.1. Таблица 5.1 - Результаты расчётов кинематических характеристик кулачкового механизма
 5.4 Определение основных размеров 5.4 Определение основных размеровМинимальный радиус-вектор R0центрового профиля кулачка определяются из условия, что угол давления 0 в проектируемом механизме во всех положениях не должен превышать максимально допустимой величины на фазе удаления. Решение указанной задачи выполняем графическим методом. Для этого на основании графиков S(φ) и S'(φ) строим совмещённую диаграмму S'(S) для фазы удаления, при этом ординаты S' откладываются повёрнутыми на 90o в сторону вращения кулачка. К построенной кривой слева и справа проводим касательные под углами Θдоп = 25° к оси S. Ниже точки пересечения этих касательных находится зона, в которой можно выбирать центр вращения кулачка из условия Θi < Θдоп. Из чертежа при е=0мм находим R0 = OA0 5.5 Построение профиля кулачка (графический метод) Используем графический способ построения центрового профиля кулачка по точкам, применяя метод обращения движения. Выбираем масштабный коэффициент:μS = 0,25 Проводим две окружности радиуса е и Ro и вертикальную касательную к окружности радиуса е. В соответствии с графиком S(φ) наносим разметку хода толкателя А0, А1, А2, А3 ... А8 для фазы удаления. От прямой 01А8 в сторону, противоположную вращению кулачка, откладываются фазовые углы: φп=120o, φдс= 0o, φо= 120o. Дуги максимального радиуса, стягивающие фазовые углы φп и φo, делим на 8 равных частей в соответствии с графиком S(φ) и получаем точки 0, 1,2, ... 8, через которые проводим касательные к окружности радиуса е. Затем радиусами OA1, OA2, ОАз, ... OA8 проводим дуги до пересечения с соответствующими касательными в точках 0', 1', 2', ... 8', которые являются положения центра ролика в обращенном движении. Соединяя отмеченные точки плавной кривой, получаем центровой профиль кулачка для фазы удаления. Для фазы возвращения все построения выполняются аналогичным образом. Радиус ролика выбирается с учётом двух условий 1) rР < 0,4 2) rP < 0,7 pmin = N5' r р < 0,4 r р < 0,7  Принимаем радиус ролика rр = 10 мм. Принимаем радиус ролика rр = 10 мм.Действительный профиль кулачка строим в виде эквидистантной кривой по отношению к центровому профилю. Для её построения из точек центрового профиля описываем ряд дуг радиусом rр. Огибающая всех этих дуг и представляет собой действительный профиль кулачка. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
