Детали машин. Механизм двухступенчатого двухцилиндрового компрессора
 Скачать 0.86 Mb.
|
|
4.1 Проектирование схемы планетарного механизма 4.1.1 Задачи и методы синтеза планетарных механизмов Задачей синтеза, является получение требуемого передаточного отношения. Для её решения используем метод Виллиса, в основе которого лежит принцип обращения движения звеньев. Сущность этого принципа состоит в том, что сообщается дополнительное вращение всем звеньям механизма вокруг их геометрических осей со скоростью - ωн, в результате чего водило Н вращаемое со скоростью + ωн в обращенном движении будет неподвижно и все оси вращения зубчатых колес механизма также неподвижны. Передаточное отношение такой передачи можно определить по зависимостям для зубчатых передач с неподвижными геометрическими осями. 4.1.2 Исходные данные Частота вращения электродвигателя nдв = 2940 об/мин Частота вращения кривошипа n1 = 655 об/мин; Модуль зубчатых колёс планетарного механизма m = 3 мм; 4.1.3 Определение числа сателлитов и числа зубьев колёс механизма Планетарным называется механизм, в котором геометрические оси некоторых зубчатых колес являются подвижными. Общее передаточное отношение U1Н = nдв/ n1 = 2940/655 = 4,489  По теореме Виллиса  ,Откуда  Принимаем Z1 = 18, тогда Z3=18  3,489=62,8 ≈ 63. Из условия соосности  Уточним передаточное отношение  Погрешность составляет  Максимальное число сателлитов из условия соседства 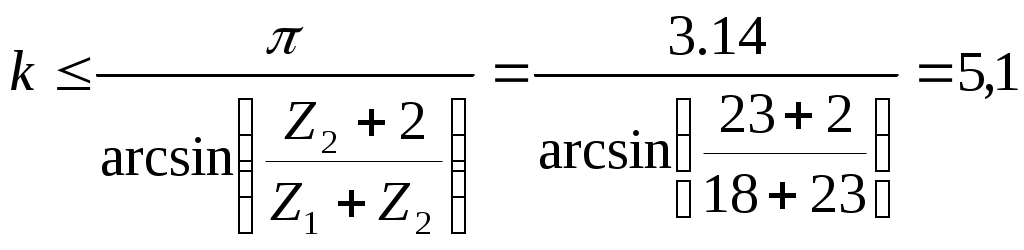 Примем число сателлитов к = 4. Условие сборки  - целое число.4.1.4 Определение диаметров начальных окружностей колёс Редуктор собирается из колес без смещения d = m1  z;d1 = 3 18 = 54 мм; d2 = 3 23 = 69 мм; d3 = 3 63 = 189 мм. Вычерчиваем схему редуктора с масштабным коэффициентом  4.2 Проектирование цилиндрической эвольвенты зубчатой передачи внешнего зацепления 4.2.1 Исходные данные Z1 = 12, Z2 = 18 - числа зубьев колёс; m = 3 мм - модуль зацепления; h*а = 1 — коэффициент высоты головки зуба; с* = 0,25 - коэффициент радиального зазора; α = 20° - угол профиля исходного контура. 4.2.2 выбор коэффициентов смещения х1 и х2 исходного контура Коэффициенты смещения х1 и х2 и должны соответствовать условию (при отсутствии подрезания зубьев): х1> xminl ; х2 > xmin2. Минимальное число зубьев  хmin1 и xmin2 определяем по формуле  ; Выбираем коэффициенты смещения х1 и х2 для силовых передач при свободном выборе межосевого расстояния х1 = 0.2; х2 = 0. 4.2.3 Расчёт параметров зубчатых колёс и параметров зацепления Коэффициент суммы смещений: х∑ = х1+ х2 = 0.3 + 0 = 0.3. Угол зацепления αω  0,014904+0,00727 = 0,02218αω = 22,7о. Межосевое расстояние  Делительное межосевое расстояние передачи  Коэффициент воспринимаемого смещения y = (αω - α)/m = (45.84 - 45)/3 = 0.28. Коэффициент уравнительного смещения ∆y = х∑ - у = 0.3 - 0.28 = 0.02.  Делительные радиусы колес r1 = m Z1/2 = 3 12/2 = 18 мм;r2 = m Z2/2 = 3 18/2 = 27 мм.Радиусы начальных окружностей rω1 = m Z1/2 cosα/ cosαω = 3 12/2 cos20o/ cos22,7o = 18,33 мм;rω2 = m Z2/2 cosα/ cosαω = 3 18/2 cos20o/ cos22,7o = 27,51 мм.Радиусы вершин зубьев: ral = m (Z1/2 + ha*+ x1 - ∆y) = 3 (12/2 + 1 + 0.3 -0.02) = 21.84 мм ;ra2 = m (Z2/2 + ha*+ x2 - ∆y) = 3 (18 /2 + 1 + 0 - 0.02) = 29.94 мм.Радиусы впадин колес: rƒ1 = m (Z1/2 + x1 - ha* - с*) = 3 (12/2 + 0.3 - 1 - 0.25) = 15,15 мм;r ƒ2 = m (Z2/2 + x2 - ha* - c*) = 3 (18/2 + 0 - l - 0.25) = 23.25 мм.Высота зубьев колес h =m (2 ha* + с* - ∆y) = 3 (2 1 + 0.25 - 0.02) = 6.69 мм. Окружной делительный шаг p = π m = 3.142 3 = 9.425 мм.Угловой шаг  τ1 = 2 π/Z1 = 2 180°/12 = 30°;τ2 = 2 π/Z2 = 2 180°/18 = 20°.Толщины зубьев по делительной окружности S1 = m (π/2 + 2x1 - tgα) = 3 (3.142/2 + 2 - 0.3 - tg20°) = 6,71 мм;S2 = m (π/2 + 2x2 - tgα) = 3 (3.142/2 + 2 - 0 - tg20°) = 7,92 мм.Радиусы основных окружностей rb1 = r1 cosα = 18 - cos20° = 16,91 мм;rb2= r2 cosα = 27 - cos20° = 25,37 мм.Углы профиля в точке на окружности вершин αal = arccos (rb1/ra1) = arccos(16.91/21.84) = 39,26°;αa2= arccos (rb2/ra2) = arccos(25.06/29.94) = 32,07 °.Толщины зубьев по окружности вершин     Радиус кривизны эвольвенты на вершине зуба ρα1 = rb1 tgαa1 =16.91 tg39.26° = 13,82 мм; ρα2 = rb2 tgαa2 = 25.37 tg32.07° = 15,89мм.Длина линии зацепления g = αω sinαω = 45.84 sin22,7= 17,69 мм.Длина активной линии зацепления gα = ραl + ρα2 - g = 13,82 + 15,89 – 17,69 = 12,02 мм. Углы перекрытия φα1 = gα/ rb1 = 12,02/16,91 = 0.710 = 40,68; φα2 = gα/ rb2 = 12,02/25,37 = 0.473 = 27,1. Радиус кривизны эвольвенты в нижней точке активного профиля ρpl = g - ραl = 17,69 -13,82 = 3,87 мм; ρp2 = g - ρα2 = 17,69 – 15,89 = 1,8 мм. 4.2.4 Определение масштабных размеров параметров зубчатых колес Вычерчиваем эвольвентные профили зубчатых колёс в масштабе μl= 0.1-10-3 м/мм. Для этого определим масштабные размеры параметров зубчатых колес. Межосевое расстояние составит: Aω =aω / μl= 45.84/0.1 = 458,4 мм. Высота зубьев составит:  Н = h / μl=6.69/0.1 =66,9 ммАналогично находим масштабные размеры остальных параметров. Результаты расчётов приведены в таблице 4.1 Таблица 4.1 - Определение масштабных размеров
4.2.5 Оценка проектируемой передачи по качественным и геометрическим показателям Коэффициент перекрытия является характеристикой плавности работы зубчатой передачи   Коэффициент перекрытия также является отношением угла перекрытия зубчатого колеса к его угловому шагу 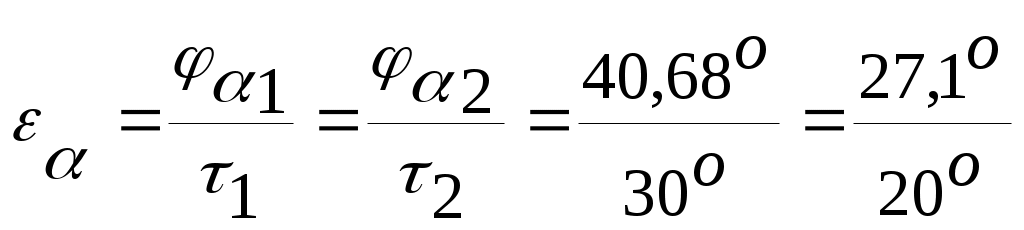 =1.36. Для прямозубых передач по ГОСТ 16532-70 рекомендуется  > 1.2. Коэффициенты толщины зубьев по окружности вершинS*a1 = Sa1 /m = 1.71/3 =1,69; S*a2= Sa2 /m = 3,06/3 =0,997.  Относительная толщина зубьев колес в пределах нормы. | ||||||||||||||||||||||||||||||||||||||||||||
