Детали машин. Механизм двухступенчатого двухцилиндрового компрессора
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
2.3  Построение планов ускорений Построение планов ускоренийПостроение плана ускорений начинаем с точки А звена ОА. Абсолютное ускорение определяется из выражения [3]:
Здесь нормальная составляющая равна по величине:
и направлена вдоль звена ОА к центру вращения (точке О). Тангенциальная составляющая:
равна 0, так как 1=const и Подставляя в формулу (7), получаем: Аналогично определяем ускорение точки С: Составляем векторное уравнение для структурной группы 23 [3]:
где  вращательном движении шатуна относительно точки А; вращательном движении шатуна относительно точки А; Решаем векторное уравнение (10) построением плана ускорений, задавшись масштабным коэффициентом а = 15 м/с2мм. Из произвольной точки - полюса плана ускорений проводим вектор а параллельно звену ОА в направлении от точки А к точке О. Величина отрезка Из точки а параллельно АВ в направлении от точки А к точке В проводим вектор нормальной составляющей Аналогично составляем и решаем векторное уравнение для структурной группы 45. Замеряем длины отрезков на плане: [ba] = 24,32 мм, [b] = 46,69 мм, [n2b] = 22,78 мм, [dc] = 24,32 мм, [d] = 35,18 мм, [n4d] = 22,78 мм. Определим величины ускорений:  м/с2; м/с2;Ускорение аs2 центра масс S2 звена 2 определяем по теореме подобия. Точки А, S2 и В лежат на одной прямой и принадлежат одному звену 2:
откуда Длины АS2 = 78,67 мм и АВ = 236 мм получены путем замера отрезков на плане положений механизма. Откладываем отрезок из полюса к точке s2. Получаем вектор ускорения центра масс звена 2 VS2. Величину этой скорости определяем из выражения аS2 = [s2]а = 45,6615 = 684,90 м/с. Ускорение аs4 центра масс S4 звена 4 определяем аналогично: аS4 = [s4]а = 42,0815 = 631,20 м/с. Определяем величину углового ускорения звеньев 2 и 4:
Аналогично строим план ускорений для остальных положений механизма. Результаты заносим в таблицы 6 и 7. Таблица 6 – Линейные ускорения звеньев для различных положений механизма
 Таблица 7 – Угловые ускорения звеньев для различных положений механизма
 3ДИНАМИЧЕСКИЙ СИНТЕЗ РЫЧАЖНОГО МЕХАНИЗМА ПО КОЭФФИЦИЕНТУ НЕРАВНОМЕРНОСТИ ДВИЖЕНИЯ Внутри цикла установившегося движения угловая скорость начального звена машины периодически изменяется из-за постоянного изменения нагрузок, что приводит к нежелательной неравномерности движения. Неравномерность движения начального звена характеризуется коэффициентом неравномерности движения , который не должен превышать допустимого значения []. Для снижения колебаний угловой скорости начального звена до допустимых пределов в механизме предусматривают маховик, который с целью уменьшения его размеров устанавливают на быстроходном валу. Динамическая модель механизма состоит из одного звена, к которому приложены движущие силы Мпд, а также приведены все силы Мпс, действующие на звенья механизма и моменты инерции звеньев Jn. 3.1Построение графика приведённого к ведущему звену момента инерции механизма За звено приведения п  ринимаем кривошип 1. Полный приведенный момент инерции для каждого положения механизма определяется по формуле: ринимаем кривошип 1. Полный приведенный момент инерции для каждого положения механизма определяется по формуле:
где Jм – приведенный момент инерции маховика; Jn – приведенный момент инерции звеньев механизма; Jnдв – приведенный момент инерции электродвигателя. Приведенный момент инерции электродвигателя определяется по формуле:
Приведенный момент инерции звеньев механизма определяем по формуле:
где mi – масса звена i; VSi – скорость центра масс звена i; i – угловая скорость звена i; 1 – угловая скорость ведущего звена; Jsi – момент инерции звена i. Для рычажного механизма компрессора формула (13) примет вид:
при этом отношения скоростей зависят от положения механизма и определяются из планов скоростей (см. раздел 2.2, таблица 3). Значения моментов инерций и масс звеньев механизма указаны в исходных данных (таблица 1): Js1 = 0,75 кгм2, Js2 = Js4 = 0,60 кгм2, m2 = m4 = 19 кг, m3 = 40 кг, m5 = 21 кг. Значения Jn для двенадцати положений кривошипа расчитанны  е по формуле (15), приведены в таблице 8. е по формуле (15), приведены в таблице 8.Таблица 8 – Приведенные моменты инерции звеньев механизма для различных положений механизма
Строим график Jn() приведен  ного момента инерции звеньев, приняв масштабные коэффициенты по осям: = 0,05 рад/мм, J = 0,05 (кгм2)/мм. ного момента инерции звеньев, приняв масштабные коэффициенты по осям: = 0,05 рад/мм, J = 0,05 (кгм2)/мм.Величину ординаты Y(J) найдем по формуле:
Значения остальных ординат, вычисленных аналогичным образом, заносим в таблицу 8. 3.2Построение графика приведенного момента сил сопротивления и движущих сил 3.2.1 По заданной диаграмме сил производственного сопротивления ступеней компрессора определим силы
где Определяем силы сопротивления для всех положений механизма, результаты заносим в таблицу 9. Таблица 9 – Силы производственного сопротивления для различных положений механизма
На плане скоростей прикладываем силу Fb в точке b, а F5 в точке d.  3.2.2 Определяем силы тяжести звеньев рычажного механизма: 3.2.2 Определяем силы тяжести звеньев рычажного механизма:G2 = m2g = 229,8 = 215,6 H; G4 = m4g = 229,8 = 215,6 H; G3 = m4g = 429,8 = 411,6 H; G5 = m5g = 299,8 = 284,2 H, где g = 9,8 м/с2 – ускорение свободного падения. На плане скоростей прикладываем силу G2 в точке S2, G4 в точке S4, G3 в точке b и G5 в точке d. 3.2.3 В точке а прикладываем приведенную силу Pn перпендикулярно (pa), модуль и направление которой найдем по теореме Жуковского. Для всех положений механизма приведенную силу определяем по формуле:
где Так для положения 7 (1 = 210) по формуле (18) имеем: Аналогично находим приведенную силу для остальных положений, результаты вычислений заносим в таблицу 10. Таблица 10 – Приведенная сила и приведенный момент сил сопротивления для различных положений механизма
3.2.4 Приведенный момент сил сопротивления определяем по формуле:
Для положения 7 (1 = 210) получим: Мс7 = 10915,660,14 = 1528,19 Нм. Аналогично находим значения приведенного момента сил сопротивления для всех указанных положений механизма, результаты вычислений заносим в таблицу 10. Для построения графика приведенного момента сил сопротивления принимае  м масштабные коэффициенты по осям: = 0,05 рад/мм, м = 50 (Нм)/мм. м масштабные коэффициенты по осям: = 0,05 рад/мм, м = 50 (Нм)/мм.Величину ординаты Y(M) найдем по формуле: Для положения 7: Значения остальных ординат приведены в таблице 10. 3.3Построение графика работ сил сопротивления и движущих сил 3.3.1 График работы, сил сопротивления Ас(1) строим методом графического интегрирования графика момента сил сопротивления Мс(1). Возьмем отрезок интегрирования (РО) = 40 мм, тогда получим масштабный коэффициент: А = М (РО) = 50 0,05 40 = 100 Дж/мм 3.3.2 График работы движущих сил Ад(1) строим в виде отрезка, соединяющего положения 0 и 12 механизма, т.к. по условию момент движущих сил Мд(1) является постоянным и, за время одного цикла установившегося движения, работа движущих сил равна работе сил сопротивления. Ад = Ас = Y(А)А = 111,93 100 = 11193 Дж. 3.3.3 График момента движущих сил Мд(1) строим путем графического дифференцирования графика Ад(1), для чего из точки Р проводим к оси ординат графика Мс(1) луч, параллельный прямой графика Ад(1).  Модуль момента движущих сил определяем из выражения: Мд = Y(Мд)М = 35,63 50 = 1781,5 Нм. 3.4Построение графика изменений кинетической энергии механизма и диаграммы Виттенбауэра 3.4.1 График изменения кинетической энергии 1 строим путем вычитания из ординат графика Ад(1) соответствующие ординаты графика Ас(1). Масштабный коэффициент при этом равен Т = А = 100 Дж/мм. 3.4.2 Диаграмму Виттенбауэра (диаграмму “энергия – масса”) Jn) строим путем исключения параметра 1 из графиков 1 и Jn1. Масштабные коэффициенты по осям диаграммы Виттенбауэра равны Т = 100 Дж/мм; J = 0,05 (м2кг)/мм. 3.5Определение момента инерции маховика 3.5.1 Проведем две касательные к диаграмме Виттенбауэра, образующие с осью Jn углы max и min, тангенсы которых найдем по формулам:
где = 1/80 – коэффициент неравномерности вращения коленчатого вала, 1 – среднее значение угловой скорости коленчатого вала в режиме установившегося движения. max = 52,02.
min = 51,35.  3.5.2 Найдем приведенный к валу кривошипа момент инерции маховика: 3.5.2 Найдем приведенный к валу кривошипа момент инерции маховика:
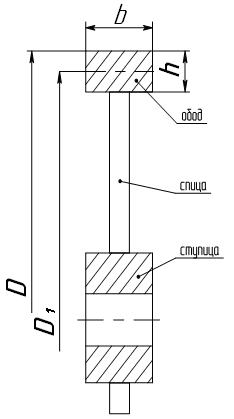
где (KL) – отрезок на оси ординат графика Jn), отсекаемый касательными к диаграмме “энергия – масса”. 3.6Определение параметров маховика 3.6.1 Для стального маховика примем плотность = 7800 кг/м. Также примем соотношения: b = 0,5 м; h = 0,1 м.
Подставим G в формулу (23), откуда получим:
Отсюда выразим приближенный диаметр D:
Если маховик ставить на ось кривошипа механизма, то он будет иметь нецелесообразные размеры и массу, потому расположил его прямо на оси двигателя. В этом случае JM – примет следующий вид:
Подставив затем JMДВ в (26) имеем:
Зная D, найдём величину D1 – средний диметр:
Найдём длину окружности маховика по формуле:
Имеем все данные для нахождения объёма V:
Находим вес маховика:
  4 Синтез зубчатых механизмов 4 Синтез зубчатых механизмов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

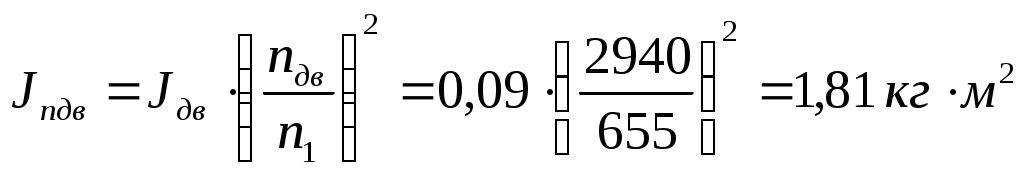 .
.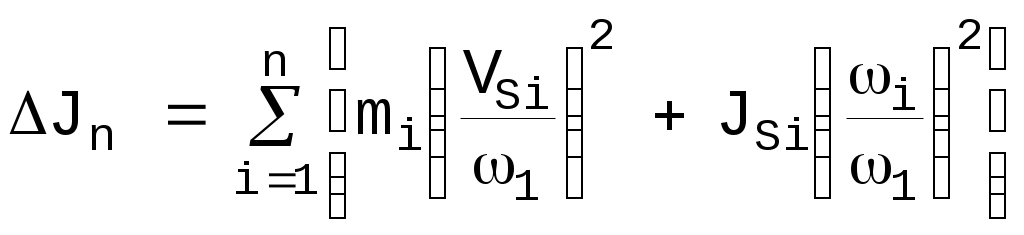 ,
,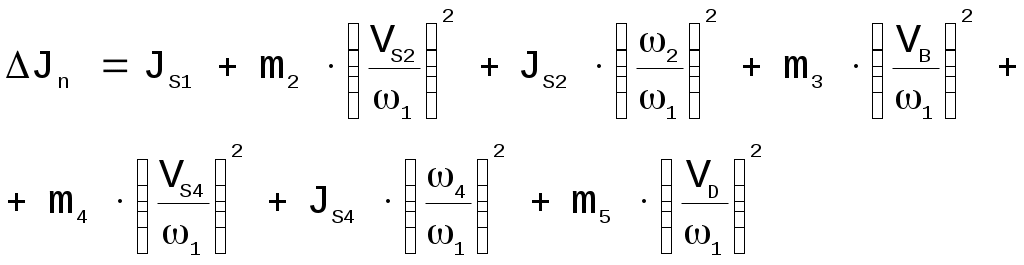 ,
,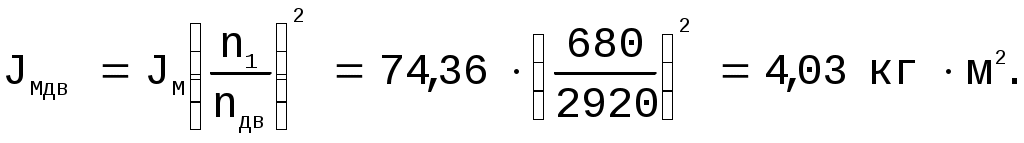
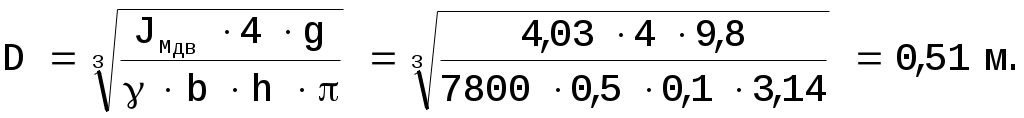
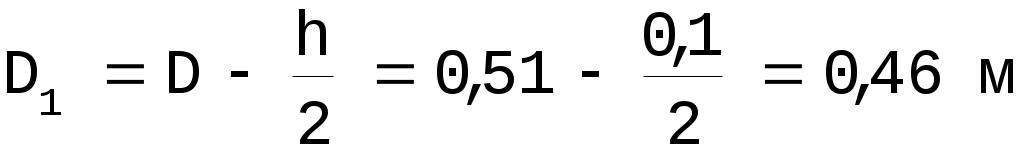 .
.