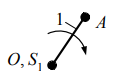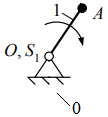Курсовая тмм. ТММ_лист2_и_другие. 2. 5 Обосновать выбор начала отсчета положений плоского рычажного механизма
 Скачать 1.36 Mb. Скачать 1.36 Mb.
|
  2.5 Обосновать выбор начала отсчета положений плоского рычажного механизма.
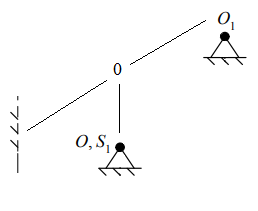
3 Кинематический анализ сложного плоского рычажного механизма 3.1 Составить векторные уравнения распределения величин скоростей между характерными точками механизма. 3.2 выбрать масштабный коэффициент скоростей. 3.3 Решая векторные уравнения, выполнить синтез планов скоростей для каждого положения начального звена. 3.4 Определить значения скоростей характерных точек, а также величины и направления действия угловых скоростей всех звеньев механизма для каждого положения начального звена. 3.5 Составить векторные уравнения распределения величин ускорений между характерными точками механизма. 3.6 Выбрать масштабный коэффициент ускорений. 3.7 Решая векторные уравнения, выполнить синтез планов ускорений для каждого положения начального звена. 3.8 Определить значения ускорений характерных точек, а также величины и направления действия угловых ускорений всех звеньев механизма для каждого положения начального звена. 4 Силовой анализ сложного плоского рычажного механизма 4.1 Определив значения и направления силовых факторов, действующих на звенья механизма, т. е. сил тяжести, сил и моментов пар сил инерции, выполнить синтез расчетной модели (схемы), установить для заданного положения механизма квазистатическое равновесие (сформировать расчетную модель (схему)). 4.2 Выполнить синтез динамической модели сложного плоского рычажного механизма для силового анализа. 4.3 Выполнить синтез повернутого плана скоростей заданного положения начального звена. 4.4 Используя теорему Жуковского,перенести все силовые факторы с расчетной модели (схемы) в одноименные точки повернутого плана скоростей. 4.5 Определить значение силового управляющего воздействия. 5 Динамический анализ сложного плоского рычажного механизма 5.1 Для каждого ползуна в соответствии с величиной фазового угла рабочего хода выявить положения механизма, в которых при определении значений приведенного момента пары сил необходимо учесть действие сил полезного сопротивления. 5.2 Выполнить синтез динамической модели сложного плоского рычажного механизма для динамического анализа. 5.3 Синтез диаграммы приведенного момента сил механизма. 5.3.1 Используя следствие из теоремы Жуковского, перенести все силовые факторы, действующие на звенья в одноименные точки действительного плана скоростей для каждого положения начального звена. 5.3.2 Выполнив синтез расчетных моделей, установить статическое равновесие и вычислить величину уравновешивающей силы для каждого положения механизма. 5.3.3 Определить значения приведенной силы и приведенного момента пар сил для каждого положения начального звена. 5.3.4 Выбрав масштабные коэффициенты осей приведенных моментов пар сил и угла поворота звена приведения, выполнить синтез диаграммы приведенных моментов пар сил сопротивления и приведенных моментов пар движущих сил. 5.4 Осуществив преобразования диаграммы приведенных моментов пар сил, выполнить синтез диаграммы работ и вычислить значение масштабного коэффициента оси работ, а также работу для каждого положения начального звена. 5.5 выбрав значение масштабного коэффициента оси изменения кинетической энергии (разности работ), выполнить синтез диаграммы изменения кинетической энергии (разности работ), используя метод графического вычитания. 5.6 Синтез диаграммы приведенного момента инерции механизма. 5.6.1 Представить приведенный момент инерции механизма в виде суммы постоянной и переменной частей. 5.6.2 Представив постоянную часть приведенного момента инерции механизма в виде суммы приведенных моментов инерции элементов привода: энергетическая машина, передаточный механизм и рабочая машина, определить ее значение, а также выбрать электродвигатель. 5.6.3 Вывести уравнение и рассчитать значения переменной части приведенного момента инерции для каждого положения механизма. 5.6.4 Определить величину приведенного момента инерции и приведенной массы для каждого положения механизма. 5.6.5 Определив значения масштабных коэффициентов осей приведенного момента инерции и угла поворота звена приведения, выполнить синтез диаграмм приведенного момента инерции и приведенной массы механизма. 5.7 Методом графического исключения угла поворота звена приведения, выполнить синтез диаграмм «энергия-приведенный момент инерции» и «энергия-масса». 5.8 Вычислив значения углов наклона, провести касательные к замкнутой кривой на диаграммах «энергия-приведенный момент инерции» и «энергия-масса». 5.9 Определить значение момента инерции маховой массы. 1 Структурный анализ сложного плоского рычажного механизма 1.1 Структурная схема сложного плоского рычажного механизма представлена на рисунке 1.1, а. 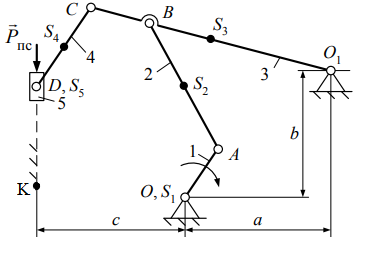 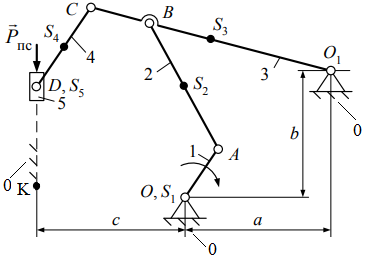 а б а бРисунок 1.1 – Структурная схема сложного плоского рычажного механизма Все элементы заданной структуры механизма, изображенные со штриховкой под 45̊, относим к одному звену (стойка) и обозначаем каждый из них цифрой 0 (рис. 1.1, б). 1.2 По условию задания раздела 1 механизм является плоским механизмом, следовательно, для определения его подвижности выбираем структурную формулу П.Л. Чебышева: где n – число подвижных звеньев, содержащихся в структуре механизма; p5, p4 – число кинематических пар пятого и четвертого класса. 1.3 Определяем название, назначение, вид совершаемого движения и количество вершин подвижных звеньев, содержащихся в структуре механизма. Результаты представлены в виде таблицы 1.1. Таблица 1.1 - Звенья механизма и их свойства
Окончание таблицы 1.1
Анализ табл. 1.1 показывает, что структура механизма содержит пять простых подвижных звена с двумя вершинами. Кривошип 1 является начальным, а ползун 5 соответствует выходному звену. 1.4 Определяем название, класс, подвижность, вид контакта и замыкания всех кинематических пар. Результаты представлены в виде таблицы 1.2. Таблица 1.2 - Кинематические пары и их свойства
Окончание таблицы 1.2
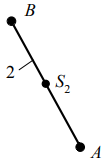
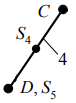
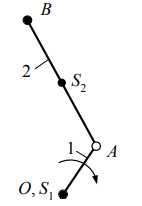
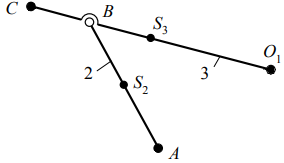
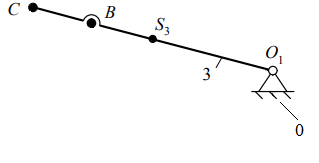
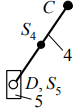
1.5 Анализируя данные таблицы 1.2, делаем вывод, что структура механизма реализована одной кинематической цепью, обладающей следующими свойствами: а) по конструктивному исполнению – сложная, так как структура механизма содержит коромысло 3, входящие в состав трех кинематических пар; б) по взаимодействию звеньев – замкнутая, так как в состав структуры механизма не входят звенья, имеющие свободный элемент, не взаимодействующий с другими звеньями и не образующий с ними кинематической пары. Согласно данным табл. 1.1 стойка представлена тремя элементами: двумя шарнирно - неподвижными опорами и одной направляющей (прямая DK). 1.6 Анализ данных табл. 1.1 также показывает, что структура механизма содержит пять подвижных звеньев 1, 2, 3, 4 и 5, следовательно, n= 5. В соответствии с табл. 1.2 показывает, что звенья, содержащиеся в структуре механизма, образуют между собой семь пар пятого класса, тогда p5= 7, а p4= 0. Подставив значения коэффициентов в формулу (1.1), получим Результат означает, что для математического описания взаимного расположения звеньев механизма на плоскости достаточно одной обобщенной координаты. 1.7 С целью определения числа и свойств структурных групп и первичных механизмов продолжим анализ структуры механизма, используя модель Ассура. Для этого начиная с выходного звена (ползун 5) разбиваем структуру механизма на группы звеньев. При этом руководствуемся следующим правилом: если выделенная группа звеньев обладает совместно подвижностью, равной нулю, то эта группа звеньев является структурной группой; если подвижность больше нуля, тогда это первичный механизм. Группа звеньев 4-5 представленная на рисунке 1.2 состоит из двух подвижных звеньев: шатуна 4 и ползуна 5, и двух поводков: коромысло 3 и направляющей 0 (прямая DK). Эти звенья образуют между собой три кинематические пары пятого класса с подвижностью, равной единице, т.е. пары 3 – 4 и 4 – 5 вращательные, а пара 5 – 0 поступательная. Тогда коэффициенты структурной формулы (1.1) принимают следующие значения: n= 2,p5= 3,p4= 0. Подставив значения коэффициентов в структурную формулу (1.1), получим Результат означает, что группа звеньев 4 – 5 является структурной группой. Значения коэффициентов указывают на то, что класс структурной группы второй. Наличие двух поводков свидетельствует о втором порядке. Из первых букв названий кинематических пар составляем структурную формулу. В результате получаем ВВП, следовательно, вид второй. 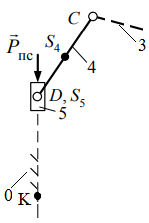 Рисунок 1.2 – Структурная группа 4-5 Группа звеньев 2-3 изображенная на рисунке 1.3, содержащаяся в структуре механизма, состоит из двух подвижных звеньев: шатуна 2 и коромысла 3, и двух поводков: кривошипа 1 и элемента стойки 0 (шарнирно-неподвижная опора). Эти звенья образуют между собой три вращательные пары пятого класса с подвижностью, равной единице: 1-2, 3-4, 3-0. Тогда коэффициенты структурной формулы (1.1) принимают следующие значения: |