Курсовая тмм. ТММ_лист2_и_другие. 2. 5 Обосновать выбор начала отсчета положений плоского рычажного механизма
 Скачать 1.36 Mb.
|
n = 2, p5 = 3, p4 = 0.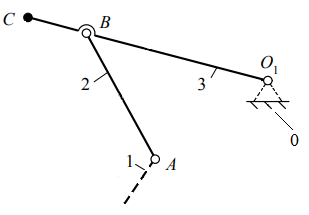 Рисунок 1.3 – Структурная группа 2-3 Подставив значения коэффициентов в структурную формулу (1.1), получим  .Результат означает, что группа звеньев 2-3 является структурной группой. Значения коэффициентов указывают на то, что класс структурной группы второй. Наличие двух поводков свидетельствует о втором порядке. Из первых букв названий кинематических пар составляем структурную формулу. В результате получаем ВВВ, следовательно, вид первый. Группа звеньев 0-1 представленная на рисунке 1.4 состоит из подвижного кривошипа 1 и стойки 0, образующих одну вращательную кинематическую пару пятого класса 0-1 с подвижностью, равной единице, тогда n = 1, p5 = 1, а p4 = 0. 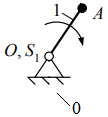 Рисунок 1.4 – Первичный механизм 0-1 Подставив значения коэффициентов в структурную формулу (1.1), получим  .Результат означает, что группа звеньев 0-1 не является структурной группой, а представляет собой первичный механизм, подвижность которого равна единице, т.е. существует одна обобщенная координата, позволяющая математически описать возможные положения кривошипа 1 на плоскости в любой момент времени. 1.8 Из проведенного анализа (пункт 1.7) следует, что механизма состоит из первичного механизма с подвижностью, равной единице, и двух структурных групп второго класса второго порядка первого вида и второго класса второго порядка второго вида (рис. 1.5) 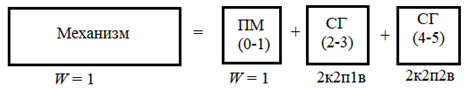 Рисунок 1.5 – Модель состава структуры механизма Анализ модели состава структуры (рис. 1.5) показывает, что в наличии имеется только структурные группы второго класса, следовательно, сложный плоский рычажный механизм является механизмом второго класса. 1.9 Анализ модели состава структуры (рис. 1.5) также показывает, что подвижность механизма определяется подвижностью первичного механизма, входящего в состав его структуры, т. е. равна единице, что соответствует результату, полученному по формуле П. Л. Чебышева в пункте 1.6. 2 Метрический синтез сложного плоского рычажного механизма 2.1 За характерные точки принимаем: а) геометрические центры кинематических пар – точки A, B, C, D, O, O1; б) центры масс звеньев – точки S1, S2, S3, S4, S5. Траектории движения характерных точек определяем с учетом данных табл. 1.3 раздел 1: Точки O, O1 и K принадлежат элементам стойки 0 (шарнирно-неподвижным опорам), т. е. являются неподвижными точками, следовательно, траекториями движения не обладают. Точка S1 по условию задания совпадает с точкой О, следовательно, тоже является не подвижной точкой и траекторией движения не обладает. Точка А принадлежит кривошипу 1, т. е. совершает вращательные движения вокруг оси проходящей через неподвижную точку O, следовательно, траекторией движения является замкнутая кривая второго порядка (окружность) с радиусом равным длине отрезка |OA|. Точки B, Cи S3 принадлежат коромыслу 3, т. е. совершают вращательные движения вокруг оси, проходящей через неподвижную точку O1, следовательно, траекторией движения являются кривые второго порядка (дуги окружностей) с радиусом, равным длине отрезка |O1B|, |O1C| и |O1S3|. Точки D и S5 совпадают и принадлежат ползуну 5, т. е. совершают поступательные движения вдоль направляющей 0 (элемент стойки), следовательно, траекторией движения является прямая, проходящая параллельно прямой DK. Точка S2 принадлежит шатуну 2, т. е. совершает сложное движение, следовательно, траекторией движения этой точки является кривая второго порядка, конкретный вид которой по условиям задания раздела 2 установить невозможно. Точка S4 принадлежит шатуну 4, т. е. совершает сложное движение, следовательно, траекторией движения этой точки является кривая второго порядка, конкретный вид которой по условиям задания раздела 2 установить невозможно. 2.2 Определяем масштабный коэффициент длин 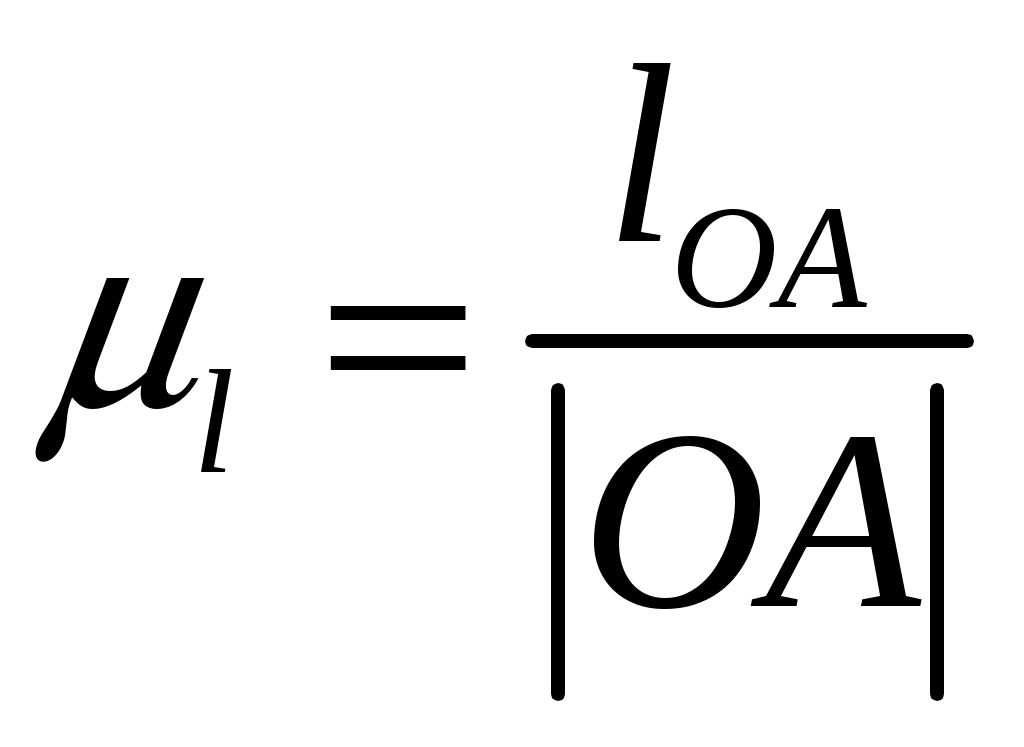 , (2.1)где lOA - действительная длина кривошипа 1, м; |OA| - длина произвольно выбранного отрезка, мм. Примем |OA| = 36 м, тогда по формуле (2.1) получим  .2.3 Переводим все заданные геометрические параметры механизма, имеющие размерность длин, м, в масштабный коэффициент, используя выражение  , (2.2)где li– заданная длина i- го звена механизма, м. Подставляя значения заданных геометрических параметров механизма в формулу (2.2), получим  мм, мм, мм, мм, мм, мм, мм, мм, мм, мм.2.4 Определяем радиусы приближения  и удаления   , (2.3) , (2.4)где |AB|, |OA| – отрезки, пропорциональные длинам шатуна 2 и кривошипа 1 в масштабном коэффициенте длин. Используя данные полученные в п. 2.2 и 2.3, по формулам (2.3) и (2.4) будем иметь  мм, мм,По полученным величинам в выбранном масштабном коэффициенте длин реализуем метрический синтез кинематических схем для крайних положений механизма (рис. 2.1). 2.5 На полученное графическое построение кинематических схем механизма наносим вектор силы полезного сопротивления 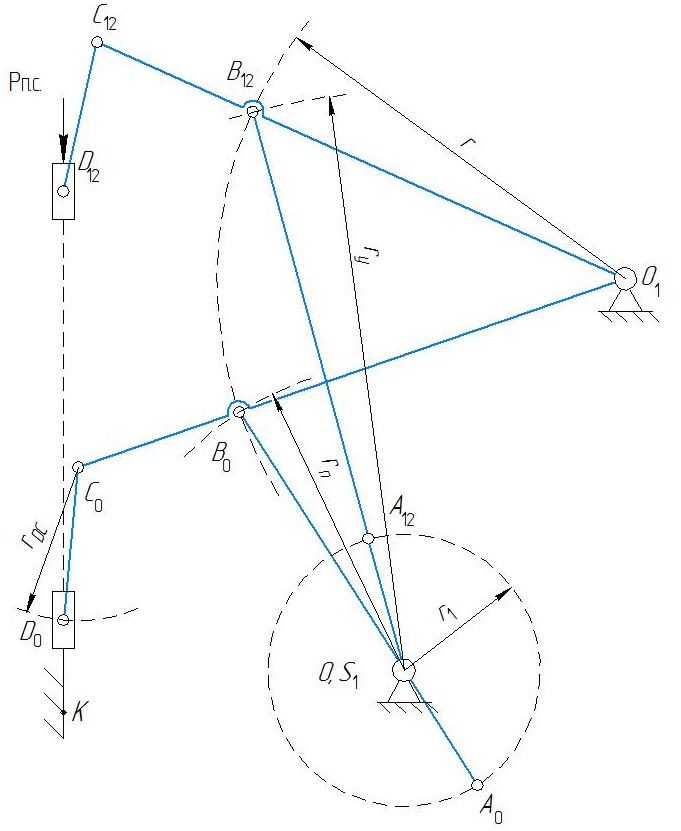 в соответствии с заданными условиями (рис. 2.1). Рисунок 2.1 – Метрический синтез кинематических схем для крайних положений механизма. За начало отсчета положений механизма принимает точку А0, а нулевым положением будем считать крайнее положение механизма, которое соответствует точке D0, полученной пересечением дуги радиусом rDC с направляющей 0, так как, начиная из этого положения движение ползуна 5 в следующий момент времени будет осуществляться в направлении, являющимся противоположным по отношению к направлению действия вектора силы полезного сопротивления (рис. 2.1).2.6 Условие эффективной эксплуатации плоских рычажных механизмов любого вида  , (2.5)где φр.х и φх.х – фазовые углы рабочего и холостого ходов. Анализируя план положений механизма, видим, что период движения механизма для ползуна 5 содержит: фазовый угол рабочего хода φр.х = 197,38° и протекающий с 0 по 12 положения кривошипа 1, а также фазовый угол холостого хода φх.х = 162,62° и протекающий с 12 по 0 положения механизма (рис. 2.2). Положения 0 и 12 являются крайними. 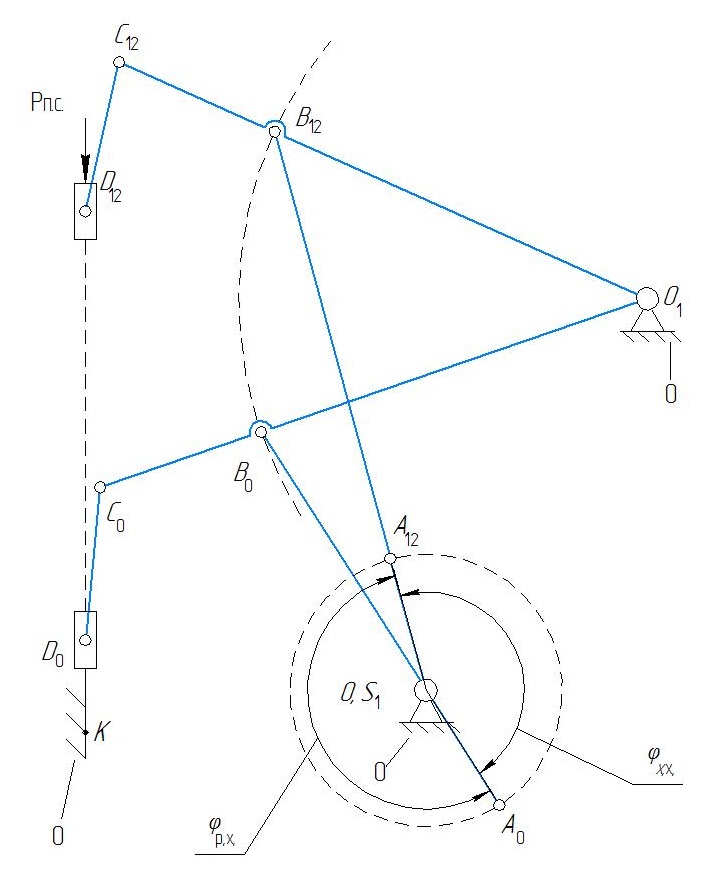 Рисунок 2.2 – Схема определения фазовых углов механизма Подставив в неравенство (2.6) выявленные величины, получим  следовательно, условие выполняется. 2.7 Ход механизма вычисляем по формулам  (2.5)где |В0В12| – длина отрезка между крайними положениями ползуна 5, мм. Замерив длину отрезка между крайними положениями ползуна 5 (рис. 2.3) по формуле (2.5), получим 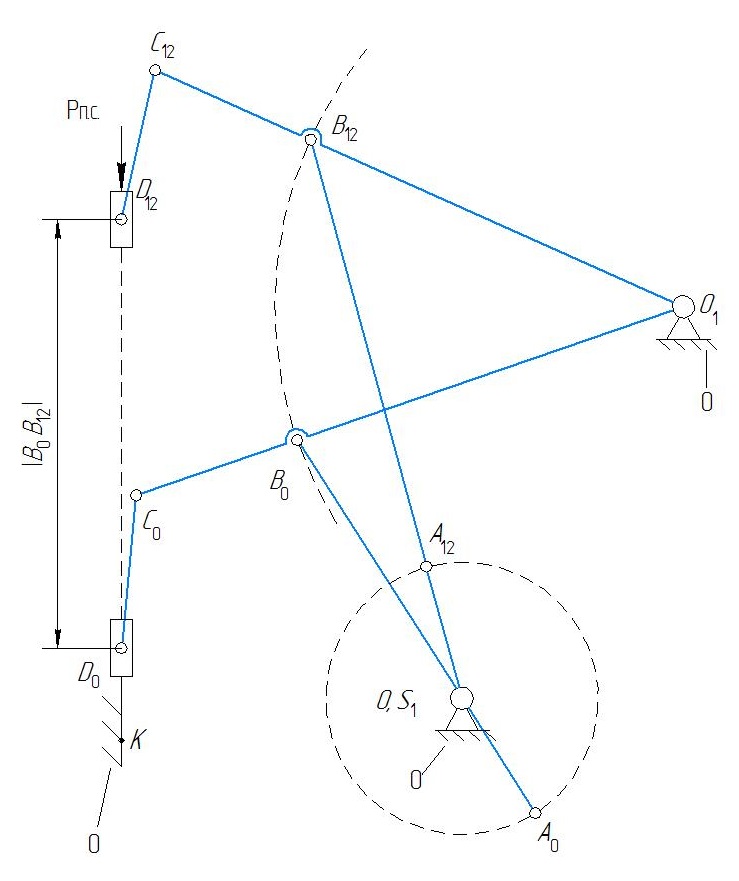 м. Рисунок 2.3 – Схема определения хода механизма Коэффициент неравномерности (изменения) средней скорости должен удовлетворять следующему условию  , (2.7)Коэффициент неравномерности средней скорости определяем по выражению 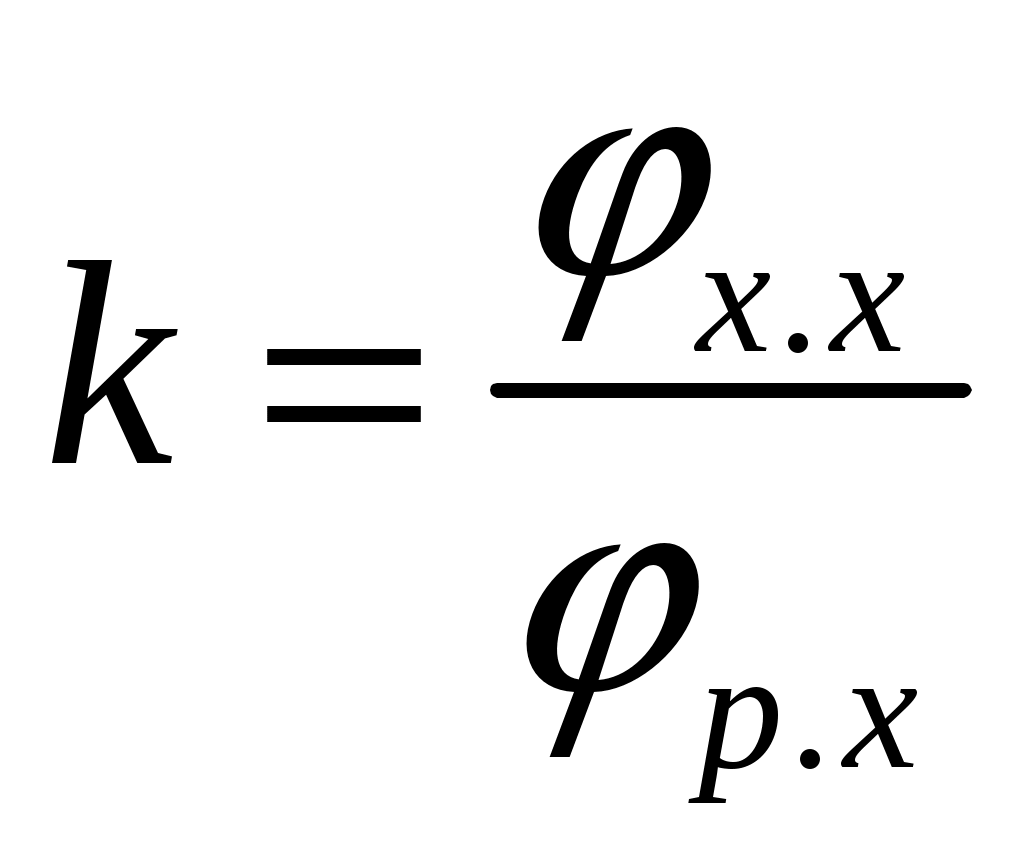 , (2.8)С учетом значений фазовых углов, выявленных в пункте 2.6 по формуле (2.8) получим  Подставив в неравенство (2.7) выявленное значение коэффициента неравномерности средней скорости, будем иметь  следовательно, условие выполняется. 2.8 Условиями задания раздела 2 задано, что кривошип 1 совершает равномерные вращательные движения, т. е. угловая скорость этого звена ω1 = const. Это означает, что за одинаковые промежутки времени кривошип 1 будет совершать равные угловые перемещения, тогда, от выбранного начала отсчета (точка А0) в заданном направлении вращения кривошипа 1 делим траекторию движения точки А (окружность радиусом r1) на двенадцать частей через 300. Полученные точки А нумеруем по порядку от 0 до 12. Добавив условные изображения кинематических пар, а также шатуна 2, коромысла 3, шатуна 4 и ползуна 5, получим кинематические схемы механизма для каждого положения кривошипа 1, метрический синтез которых выполнен в выбранном масштабном коэффициенте длин. В результате выполненных действий получаем план положений механизма, который приводим на листе 1 графической части. 3 Кинематический анализ сложного плоского рычажного механизма 3.1 Составляем векторные уравнения распределения величин скоростей между характерными точками механизма, выбор которых реализуем согласно п. 2.1 раздела 2. Точка O принадлежит элементу стойки 0 (шарнирно-неподвижной опоре), т. е, является неподвижной точкой, следовательно, скорость этой точки равна нулю в любой момент времени, т. е. VO = 0. Вектор скорости точки А, принадлежащей кривошипу 1, представляет собой геометрическую сумму вектора скорости точки O и вектора скорости относительного вращательного движения точки А вокруг оси, проходящей через неподвижную точку О  . (3.1)Первое слагаемое в уравнении (3.1) является точечным вектором, так как VO = 0. Линия действия второго слагаемого в уравнении (3.1) вектора относительной скорости является перпендикуляром к оси кривошипа 1, т. е.  , а направление действия этого вектора совпадает с направлением вращения этого звена.Решение уравнения (3.1) позволит определить положение точки a в составе плана скоростей, а также выявить значение скорости точки А и направление действия вектора этого параметра. Вектор скорости точки В, принадлежащей шатуну 2, представляет собой геометрическую сумму вектора скорости точки А и вектора скорости относительного вращательного движения точки В вокруг оси, проходящей через условно неподвижную точку А  . (3.2)Положение точки а, являющейся вершиной вектора первого слагаемого в уравнении (3.2) в составе плана скоростей найдем в результате графического решения уравнения (3.1). Линия действия второго слагаемого в уравнении (3.2) вектора относительной скорости является перпендикуляром к оси шатуна 2, т. е.  .Вектор скорости точки В, принадлежащей коромыслу 3, представляет собой геометрическую сумму вектора скорости точки O1 и вектора скорости относительного вращательного движения точки В вокруг оси, проходящей через неподвижную точку O1  . (3.3)Точка О1 является неподвижной точкой, следовательно, скорость этой точки равна нулю, т. е.  . В этом случае первое слагаемое в уравнении (3.3) является точечным вектором. Линия действия второго слагаемого в уравнении (3.3) вектора относительной скорости является перпендикуляром к оси коромысла 3, т. е.  .Совместное решение уравнений (3.2) и (3.3) позволит определить положение точки b в составе плана скоростей, а также выявить значение скорости точки В и направление действия вектора этого параметра. Вектор скорости точки D, принадлежащей шатуну 4, представляет собой геометрическую сумму вектора скорости точки С и вектора скорости относительного вращательного движения точки D вокруг оси, проходящей через условно неподвижную точку C  (3.4)Положение точки с, являющейся вершиной вектора первого слагаемого в уравнении (3.5) в составе плана скоростей найдем в результате применения теоремы подобия. Линия действия второго слагаемого в уравнении (3.4) вектора относительной скорости является перпендикуляром к оси шатуна 4, т. е.  .Вектор скорости точки D, принадлежащий ползуну 5, представляет собой геометрическую сумму вектора скорости точки K и вектора скорости поступательного движения точки D относительного точки K  (3.5)Первое слагаемое в уравнении (3.5) является точечным вектором, так как VK = 0. Ползун 5 совершает поступательное движение вдоль направляющей 0 (элемент стойки), следовательно, линия действия второго слагаемого в уравнении (3.5) вектора относительной скорости проходит параллельно прямой KD, т. е.  .Совместное графическое решение уравнений (3.4) и (3.5) позволит определить положение точки dв составе плана скоростей, а также выявить значение скорости точки D и направление действия вектора этого параметра. 3.2 Масштабный коэффициент скоростей найдем по выражению |