Курсовая тмм. ТММ_лист2_и_другие. 2. 5 Обосновать выбор начала отсчета положений плоского рычажного механизма
 Скачать 1.36 Mb.
|
|
3.5 Составляем векторные уравнения распределения величин ускорений между характерными точками механизма, выбор которых реализуем согласно п. 2.1 раздела 2. Точка О принадлежит элементу стойки 0 (шарнирно-неподвижной опоре), т. е, является неподвижной точкой, следовательно, ускорение этой точки равно нулю в любой момент времени, т. е.  .Вектор ускорения точки А представляет собой геометрическую сумму вектора ускорения точки О, вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения точки А вокруг оси, проходящей через неподвижную точку О  , (3.29)Первое слагаемое в уравнении (3.29) является точечным вектором, так как aO = 0. Третье слагаемое в уравнении (3.29) является точечным вектором, так как  , что вытекает из условия решаемой задачи: кривошип 1 шарнирного механизма совершает равномерные вращательные движения, следовательно, угловая скорость этого звена является величиной постоянной, т. е. ω1 = const. Линия действия второго слагаемого в уравнении (3.29) вектора нормального ускорения проходит параллельно оси кривошипа 1, т. е.  .Решение уравнения (3.29) позволит определить положение точки a в составе плана ускорений, а также выявить значение абсолютного ускорения точки А и направление действия вектора этого параметра. Вектор ускорения точки В, принадлежащей шатуну 2, представляет собой геометрическую сумму вектора ускорения точки А, вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения точки В вокруг оси, проходящей через условно неподвижную точку А  , (3.30)Положение точки а, являющейся вершиной вектора первого слагаемого в уравнении (3.30) в составе плана ускорений найдем в результате решения уравнения (3.29). Линия действия второго слагаемого в уравнении (3.30) вектора нормального ускорения проходит параллельно оси шатуна 2, т. е.  . Линия действия третьего слагаемого в уравнении (3.30) вектора тангенциального ускорения является перпендикуляром к оси шатуна 2, т. е.  .Вектор ускорения точки В коромысла 3, представляет собой геометрическую сумму вектора ускорения точки О1, вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения точки В вокруг оси, проходящей через неподвижную точку О1  , (3.31)Точка О1 является неподвижной точкой, следовательно, ускорение этой точки равна нулю, т. е.  . В этом случае первое слагаемое в уравнении (3.13) является точечным вектором. Линия действия второго слагаемого в уравнении (3.31) вектора нормального ускорения проходит параллельно оси коромысла 3, т. е.  . Линия действия третьего слагаемого в уравнении (3.9) вектора тангенциального ускорения является перпендикуляром к оси коромысла 3, т. е.  .Совместное решение уравнений (3.30) и (3.31) позволит определить положение точки b в составе плана ускорений, а также выявить значение ускорения точки В и направление действия вектора этого параметра. Вектор ускорения точки D, принадлежащей шатуну 4, представляет собой геометрическую сумму вектора ускорения точки C, вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения точки D вокруг оси, проходящей через условно неподвижную точку C  , (3.32)Положение точки c, являющейся вершиной вектора первого слагаемого в уравнении (3.33) в составе плана ускорений найдем применяя теорему подобия. Линия действия второго слагаемого в уравнении (3.32) вектора нормального ускорения проходит параллельно оси шатуна 4, т. е.  . Линия действия третьего слагаемого в уравнении (3.32) вектора тангенциального ускорения является перпендикуляром к оси шатуна 4, т. е.  .Вектор ускорения точки В, принадлежащий ползуну 5, представляет собой геометрическую сумму вектора ускорения точки K и вектора ускорения поступательного движения точки D относительного точки K  (3.33)Первое слагаемое в уравнении (3.33) является точечным вектором, так как aO = 0. Ползун 5 совершает поступательное движение вдоль направляющей 0 (элемент стойки), следовательно, линия действия второго слагаемого в уравнении (3.33) вектора относительного ускорения проходит параллельно прямой KD, т. е.  .Совместное решение уравнений (3.32) и (3.33) позволит определить положение точки d в составе плана ускорений, а также выявить значение абсолютного ускорения точки D и направление действия вектора этого параметра. 3.6 Масштабный коэффициент ускорений найдем по выражению  (3.34)где  – нормальное ускорение, м/с2;|оа| – длина произвольно выбранного отрезка, изображающего в составе плана ускорений вектор нормального ускорения, мм. Нормальное ускорение найдем, используя равенство  , (3.35)здесь  – угловая скорость кривошипа 1; – длина кривошипа 1.Подставив значение угловой скорости кривошипа 1 найденную в п. 3.2 и заданную длину кривошипа в формулу (3.36), получим  Считая, что  , по формуле (3.35), будем иметь 3.7 По условиям следует, что кривошип 1 совершает равномерные вращательные движения, тогда решая графически векторные уравнения (3.29)…(3.31), выполняем синтез планов ускорений в выбранном масштабном коэффициенте для каждого положения механизма. Планы ускорений представлены на листе 1 графической части. Нормальные ускорения определим, используя следующее выражения  (3.36) (3.37) (3.38)здесь  ,  ,  ,  ,  и  – угловые скорости и длины шатуна 2, коромысла 3 и шатуна 4.Подставив найденные в п. 3.4 значения угловых скоростей и заданные длины звеньев в формулы (3.37), (3.38) и (3.39), получим  (3.39) (3.40) (3.41)Длины отрезков, изображающих в составе плана вектора нормальных ускорений, определим с учетом равенств (3.40), (3.41) и (3.42) по формулам    Для определения положений точек s1, s2, s3, s4, s5, являющихся центрами тяжести звеньев механизма в составе плана ускорений выполняем ряд дополнительных действий: В соответствии с теоремой подобия совмещаем точки s1 и s5 с точкой о на плане ускорений. Положения точек s2, s3 и s4 на плане ускорений найдем, воспользовавшись теоремой подобия, тогда по формулам (3.14), (3.15) и (3.16) получим  мм; (3.42) мм; (3.43) мм. (3.44)Используя формулы (3.37)…(3.45), вычисляем отрезки, позволяющие определить положения точек p1, р2,p3, s2, s3и s4 на планах ускорений для всех положений механизма. Результат приводим на листе 1 графической части. 3.8 Измерив на плане ускорений длины отрезков |p1b|, |p2b|, |p3c|, |ps1|, |ps2|, |ps3|, |pb|, |pc| и |pd|, определяем значения абсолютных и относительных ускорений характерных точек механизма для 7 положения механизма  (3.45) (3.46) (3.47) (3.48) (3.59) (3.60) (3.61) (3.62) (3.63)Используя формулы (3.46)…(3.54), определяем величины скоростей характерных точек для всех остальных положений механизма. Результат приводим в виде таблицы 3.1. Условиями задано, что начальное (входное) звено кривошип 1 совершает равномерные вращательные движения, т. е. угловая скорость этого звена является постоянной величиной (ω1 = const), тогда тангенциальное ускорение относительного вращательного движения точки А вокруг оси, проходящей через неподвижную точку О равно нулю, следовательно, угловое ускорение этого звена также равно нулю, так как  .Угловые ускорения шатуна 2, шатуна 4 и коромысла 3 определим по формулам 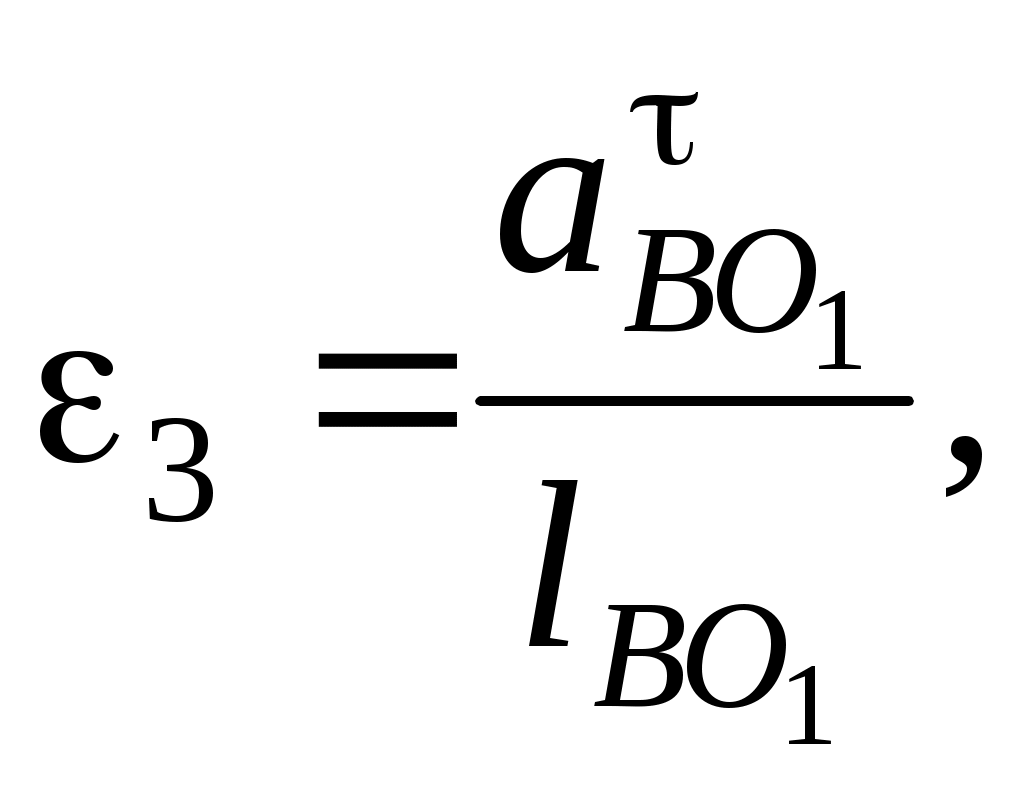 (3.64) (3.65) (3.66)Подставим значения параметров в формулы (3.33) и (3.34), получим    Направление действия углового ускорения шатуна 2 указывает вектор тангенциального ускорения  , содержащийся в уравнении (3.30) и перенесенный с плана ускорений в точку В на кинематической схеме механизма. Разрываем связи шатуна 2 с кривошипом 1 и коромыслом 3, а точку А делаем условно неподвижной. В этом случае точка В совместно шатуном 2 под действием вектора тангенциального ускорения получает возможность совершать вращательное движение в направлении действия этого вектора вокруг оси проходящей через условно неподвижную точку А. Полученное направление вращательного движения шатуна 2 будет являться направлением действий углового ускорения данного звена шарнирного механизма.Направление действия углового ускорения коромысла 3 указывает вектор тангенциального ускорения  , содержащийся в уравнении (3.31) и перенесенный с плана ускорений в точку В на кинематической схеме механизма. Разрываем связи коромысла 3 с шатуном 2, а точка O1 остается неподвижной. В этом случае точка В совместно с коромыслом 3 под действием вектора тангенциального ускорения получает возможность совершать вращательное движение в направлении действия этого вектора вокруг оси проходящей через неподвижную точку O1. Полученное направление вращательного движения коромысла 3 будет являться направлением действия углового ускорения данного звена.Направление действия углового ускорения шатуна 4 указывает вектор тангенциального ускорения  , содержащийся в уравнении (3.32) и перенесенный с плана ускорений в точку D на кинематической схеме механизма. Разрываем связи шатуна 4 с ползуном 5 и коромыслом 3, а точку С делаем условно неподвижной. В этом случае точка D совместно шатуном 4 под действием вектора тангенциального ускорения получает возможность совершать вращательное движение в направлении действия этого вектора вокруг оси проходящей через условно неподвижную точку C. Полученное направление вращательного движения шатуна 4 будет являться направлением действий углового ускорения данного звена.Ползун 3 совершает только поступательные движения, следовательно, угловое ускорение этого звена равна нулю, т. е. ε3 = 0. Используя формулы (3.64)...(3.44) определяем значения угловых ускорений звеньев для всех положений механизма. Результат представляем в виде таблицы 3.2. Таблица 3.2 – Ускорения характерных точек и угловые ускорения звеньев плоского рычажного механизма
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
, мм
, мм
, мм
, мм
, мм
, мм