Курсовая тмм. ТММ_лист2_и_другие. 2. 5 Обосновать выбор начала отсчета положений плоского рычажного механизма
 Скачать 1.36 Mb. Скачать 1.36 Mb.
|
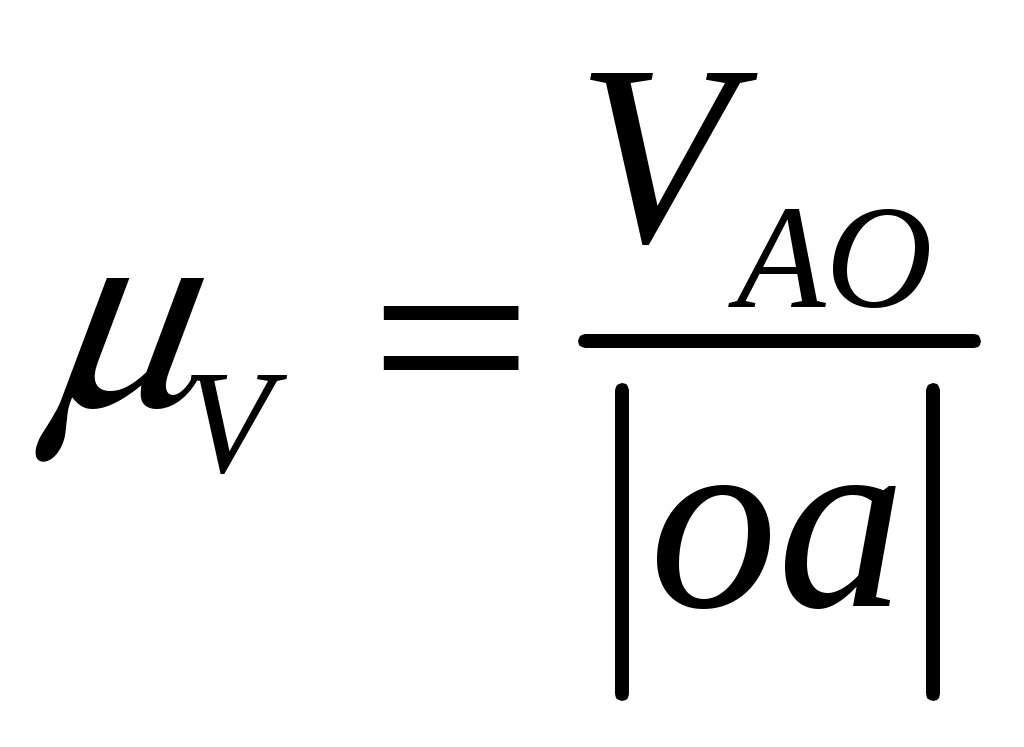 , (3.6) , (3.6)где |оа| – длина произвольно выбранного отрезка, изображающего в составе плана скоростей вектор относительной скорости, мм. Относительную скорость рассчитаем по формуле здесь ω1, lOA – угловая скорость и длина кривошипа 1. Угловую скорость кривошипа 1 найдем по выражению где n1 – число оборотов кривошипа 1, мин -1. Подставив заданные значения в формулу (3.8), будем иметь С учетом найденной угловой скорости по выражению (3.7), получим Считая, что |oa| = 90 мм, по формуле (3.6), будем иметь 3.3 По условиям задания следует, что кривошип 1 совершает равномерные вращательные движения, тогда для синтеза планов скоростей в выбранном масштабном коэффициенте решаем графически векторные уравнения (3.1)…(3.5) для каждого положения механизма. Планы скоростей представлены на листе 1 графической части. Положение точки c на планах скоростей найдем, воспользовавшись теоремой подобия 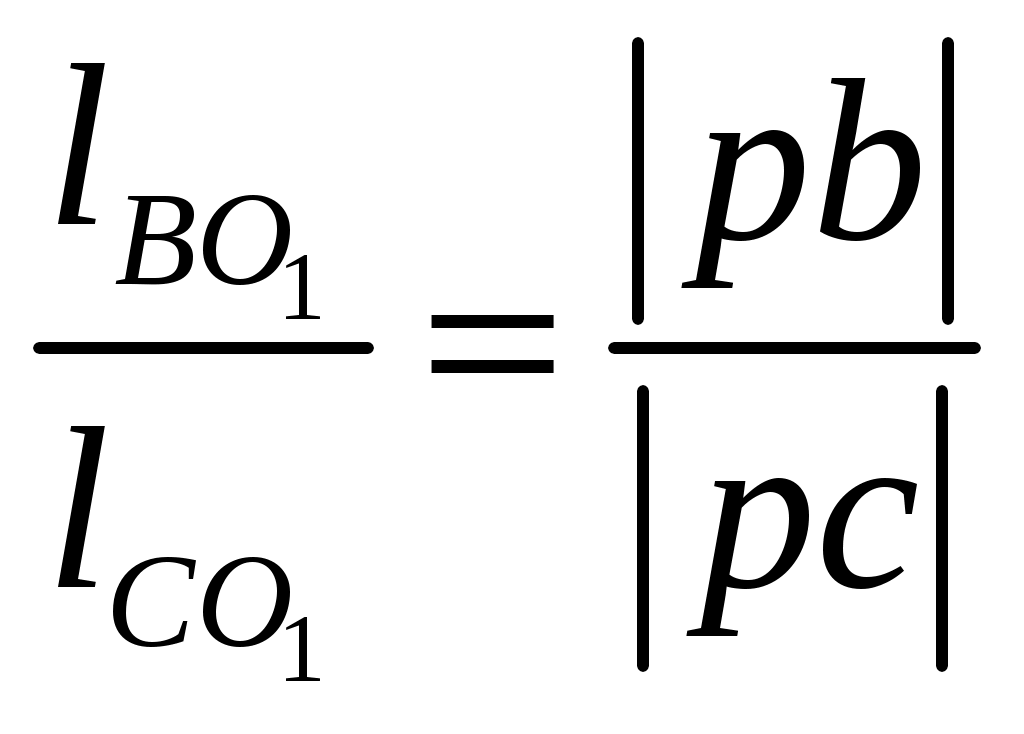 , (3.9) , (3.9)где |pb|, |pc| – длины отрезков с плана скоростей; Проведя преобразования (3.9), с учетом заданных величин для седьмого положения механизма получим 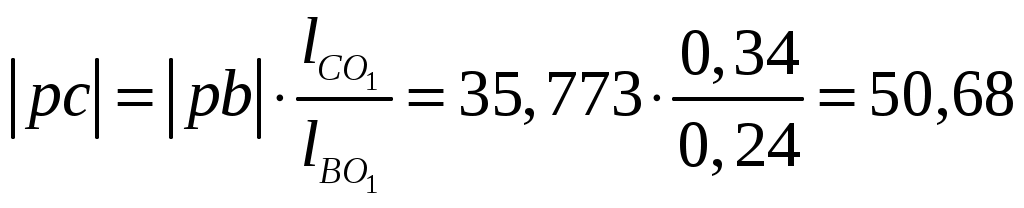 мм. (3.10) мм. (3.10)Для определения положений точек s1, s2, s3, s4 и s5 являющихся центрами тяжести звеньев механизма в составе планов скоростей выполняем ряд дополнительных действий: в соответствии с теоремой подобия совмещаем точку s1 с точкой o, а s5 с точкой dна плане скоростей. Положение точек s2, s3 и s4 на плане скоростей найдем, воспользовавшись теоремой подобия, для этого составим пропорции 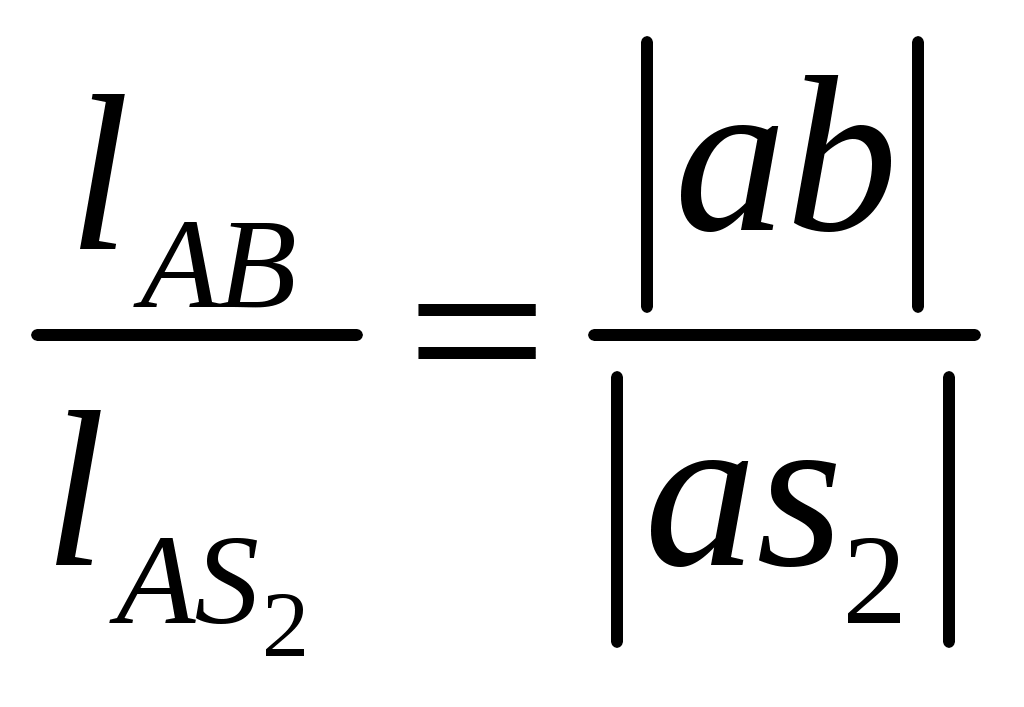 ; (3.11) ; (3.11)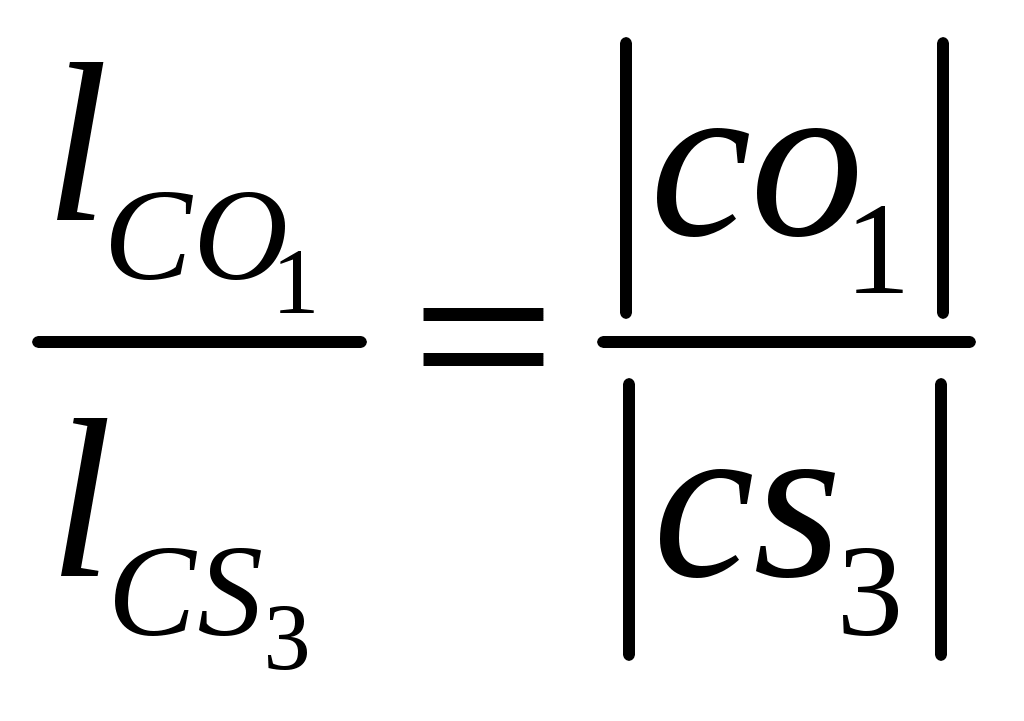 ; (3.12) ; (3.12)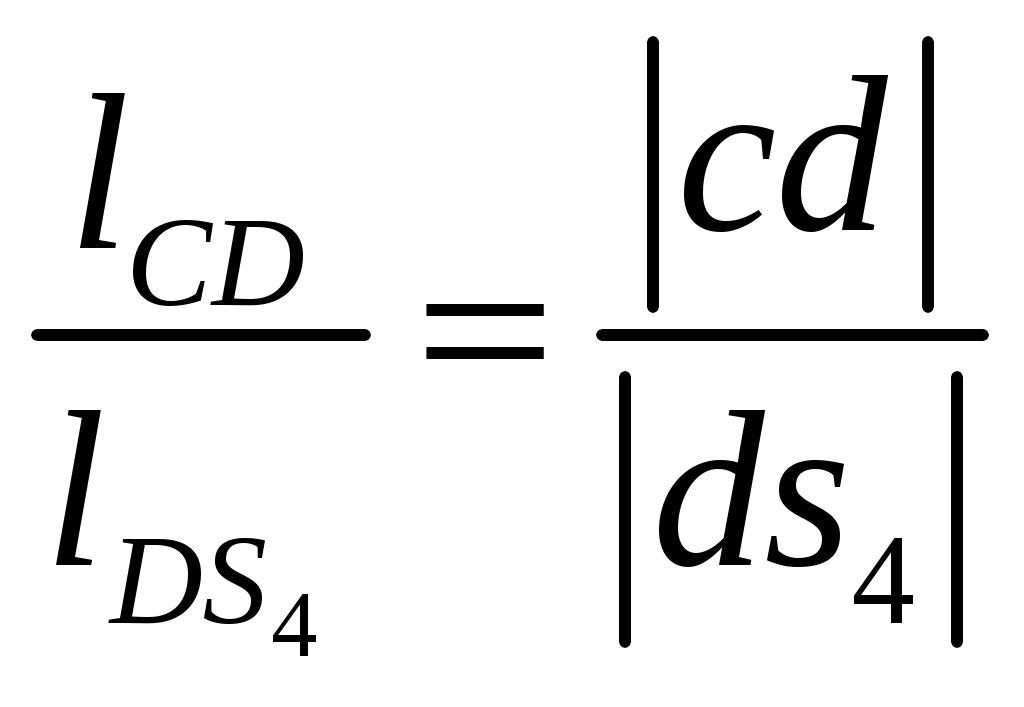 . (3.13) . (3.13)где |ab|, |as2|, |co1|, |cs3|, |cd|, |ds4| – длины отрезков с плана скоростей, мм; В результате преобразования равенств (3.11), (3.12) и (3.13), будем иметь 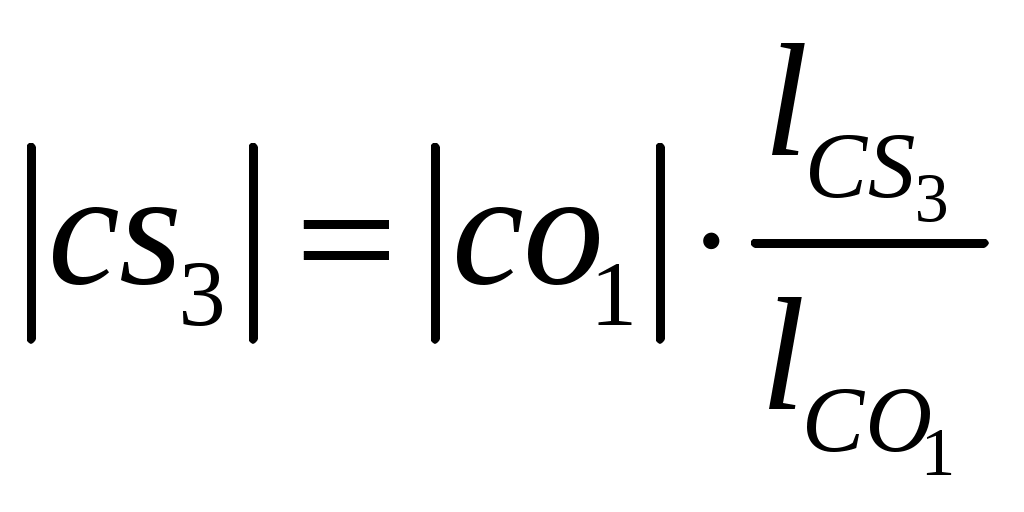 ; (3.15) ; (3.15)Измерив длины отрезков |ab|, |сo1| и |cd| на плане скоростей механизма, а также подставив в формулы (3.14), (3.15) и (3.16) заданные параметры, получим 3.4 Измерив на плане скоростей длины отрезков |ab|, |cd|, |pb|, |pc|, |pd|, |ps2|, |ps3| и |ps4|, определяем значения линейных и относительных скоростей характерных точек механизма для седьмого положения механизма. Условиями задано, что начальное (входное) звено кривошип 1 совершает равномерные вращательные движения, т. е. угловая скорость этого звена является постоянной величиной (ω1 = const), значение которой найдено в п. 3.2, а направление действия этого параметра совпадает с заданным направлением вращения данного звена. Ползун 5 совершает поступательные движения по неподвижной направляющей 0, следовательно, угловая скорость этого звена равна нулю, т. е. ω5 = 0. Угловые скорости шатуна 2 коромысла 3 и шатуна 4 определим по формулам 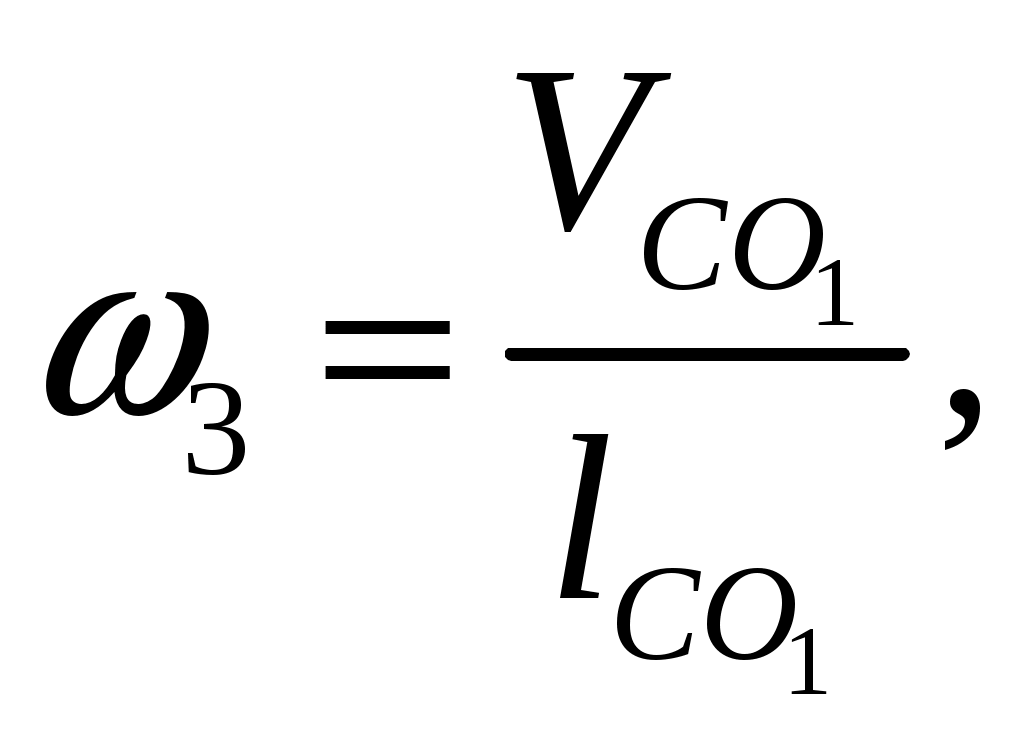 (3.27) (3.27)Подставим значения параметров в формулы (3.26), (3.27) и (3.28), получим Направление действия угловой скорости шатуна 2 указывает вектор относительной скорости VBA, содержащийся в уравнении (3.2) и перенесенный с плана скоростей в точку В на кинематической схеме механизма. Разрываем связи шатуна 2 с кривошипом 1 и коромыслом 3, а точку А делаем условно неподвижной. В этом случае точка В совместно с шатуном 2 под действием вектора относительной скорости VBA получает возможность совершать вращательное движение в направлении действия этого вектора вокруг оси проходящей через условно неподвижную точку А. Полученное направление вращательного движения шатуна 2 будет являться направлением действия угловой скорости данного звена. Направление действия угловой скорости коромысла 3 указывает вектор относительной скорости Направление действия угловой скорости шатуна 4 указывает вектор относительной скорости Используя формулы (3.26)...(3.28) определяем угловые скорости звеньев для всех положений механизма. Результат представляем в виде таблицы 3.1. Таблица 3.1 – Скорости характерных точек и угловые скорости звеньев плоского рычажного механизма
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
