УПП_Дискретная математика-1. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
 Скачать 6.65 Mb. Скачать 6.65 Mb.
|
Контрольное задание №8С помощью ДНФ и КНФ (без построения таблицы истинности) установить тип формулы (в случае выполнимой формулы установить: является ли она тождественно истиной или нейтральной). Контрольное задание №9Получить для формул из контрольного задания 8 СДНФ и СКНФ (если это возможно) с помощью равносильных преобразований (без построения таблицы истинности). Контрольное задание №10По функциям написать формулы и упростить их: 1. f (0,0,0) = f (0,0,1) = f (1,0,0) =1. 2. f (0,0,0) = f (0,0,1) = f (1,0,0) =0. 3. f (1,0,1) = f (0,1,1) = f (1,1,1) =1. 4. f (1,0,1) = f (0,1,1) = f (1,1,1) =0. 5. f (0,1,0) = f (1,1,0) = f (1,1,1) =0. 6. f (0,1,1) = f (1,0,0) = f (1,1,0) =1. 7. f (0,0,0) = f (0,1,0) = f (1,1,1) =0. 8. f (0,0,1) = f (1,0,0) = f (1,1,0) =1. 9. f (1,0,1,0) = f (0,0,1,0) =0. 10. f (1,1,0,0) = f (0,1,0,0) =1. Контрольное задание №11Упростить схемы: 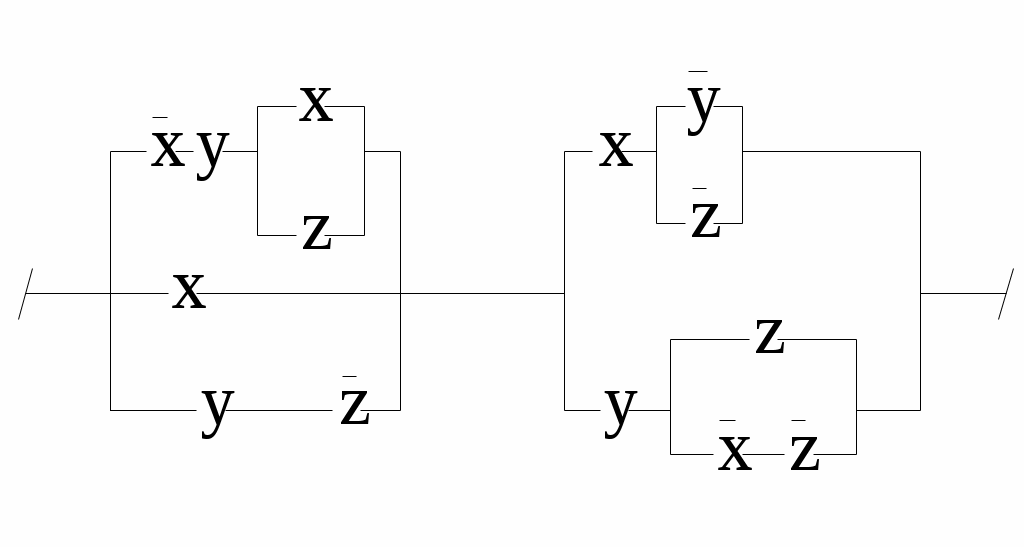 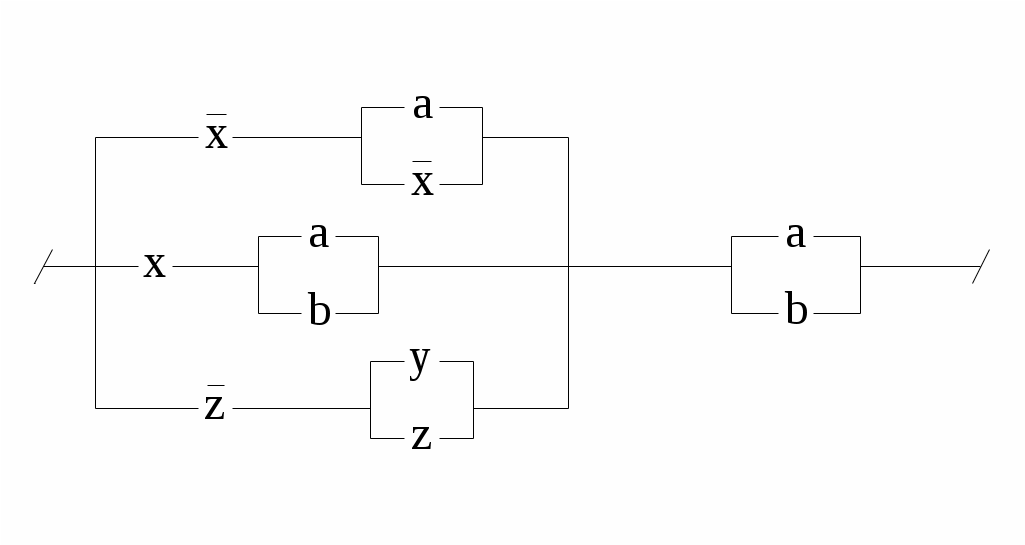 3. 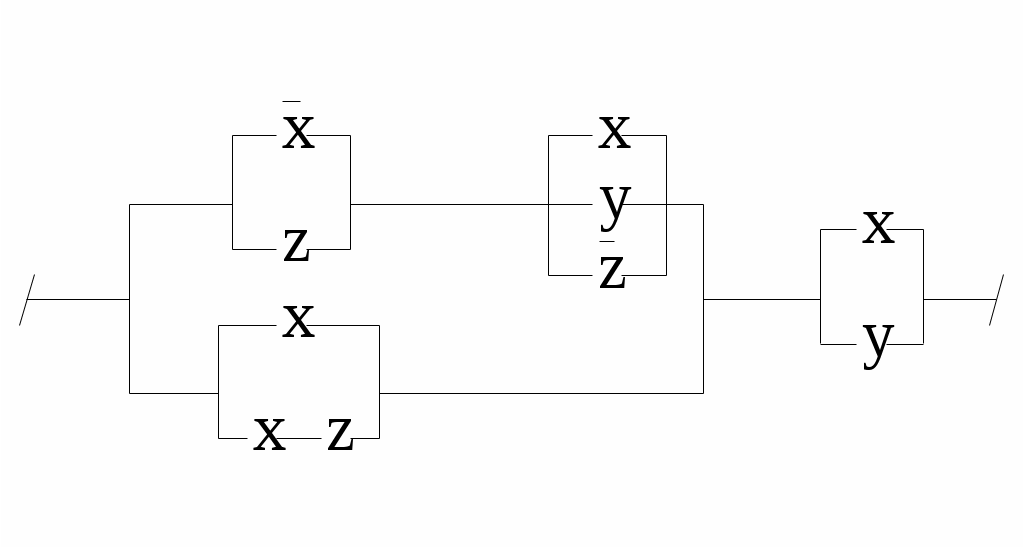 4. 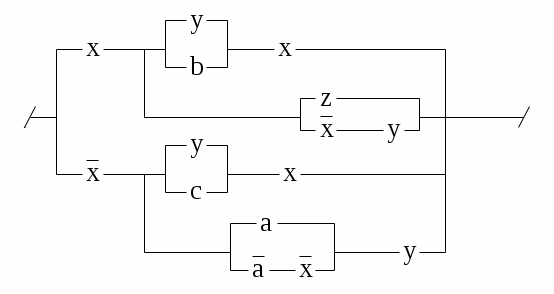 5. 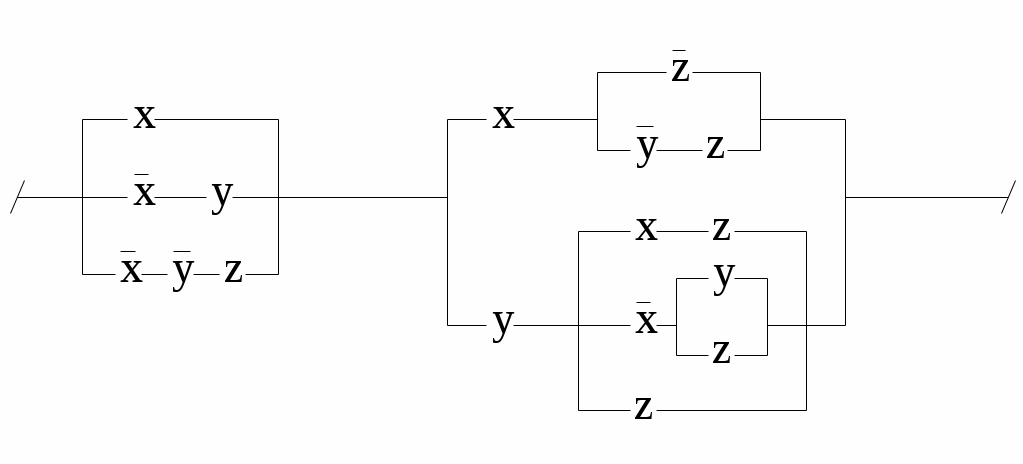 6. 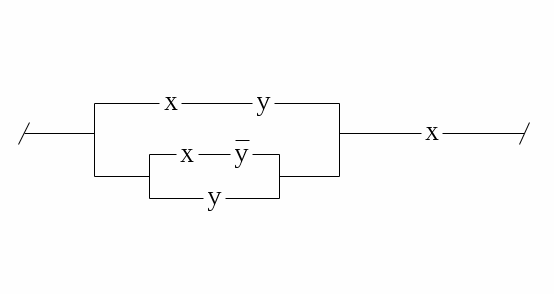 7. 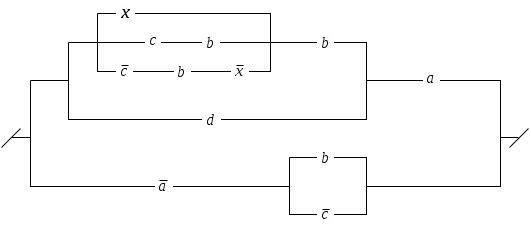 8. 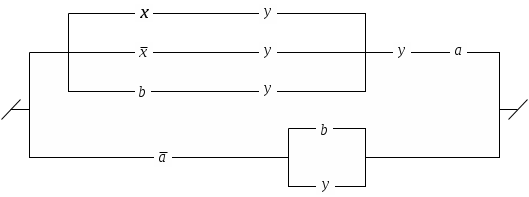 9. 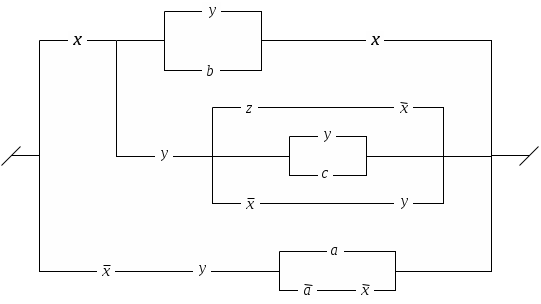 10. 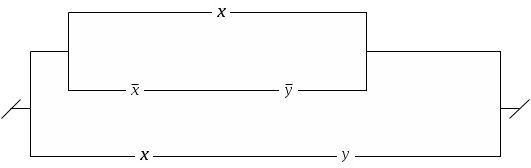 Контрольное задание №12.Ввести предикаты на соответствующих областях (возможно многоместные) и записать с их помощью высказывания: Через три произвольные точки проходит некоторая плоскость. Через три различные точки проходит некоторая плоскость. Через три различные точки проходит единственная плоскость. Через три точки, не лежащие на одной прямой, проходит некоторая плоскость. Между двумя любыми точками на прямой лежит еще хотя бы одна точка. Любая прямая лежит хотя бы в одной плоскости. Сумма двух любых четных чисел четна. Если сумма трех натуральных чисел не делится на простое число, то на него не делится, по крайней мере, одно из слагаемых. Записать в виде логики предикатов определение простого числа. записать в виде логики предикатов определение непрерывности функции. |
