УПП_Дискретная математика-1. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
 Скачать 6.65 Mb.
|
3.3. Экстремальные задачи на графахЗадача о кротчайшем пути между двумя вершинами ориентированного графа и ее экономическая интерпретация Постановка задачи Постановка задачи состоит в следующем. Задан конечный ориентированный граф G(x,гx), или G(x,u). Каждой дуге графа «u» поставлено в соответствие некоторое число l(u)0, называемое длинной дуги «u». Длинной пути называется сумма длин дуг, составляющих данный путь.  .Требуется для двух фиксированных вершин xo и xn графа G(x,u) найти самый короткий соединяющий их путь. К данной задаче может быть сведена следующая задача экономического содержания. Задана сеть дорог, соединяющих пункты xi (i=0,1,…,n). Найти путь, соединяющий пункты xo и xn, по которому можно доставить груз в кратчайшее время. При этом время доставки груза из пункта xi в xj (i,j0,…,n) задано и равно l(uij)=l(xi,xj)0. Если под длинной дуги l(xi,xj) понимать стоимость перевозки груза из пункта xi в xj, то содержание задачи составит определение такого пути из пункта xi в xj, на котором затраты на транспортировку были бы минимальными. Пример. Имеем 6 пунктов Х (x0,…,x6). Сеть дорог, связывающих эти пункты, изображена на графе (рис.3.3.1). Время доставки груза из i-го пункта в j-й, т.е. l(xi,xj), задано и изображено числом в кружке, записанным рядом с дугой (xi,xj). Так, l(x0,x1)=2, l(x0,x2)=4, l(x0,x3)=5, l(x1,x4)=3 и т.д. 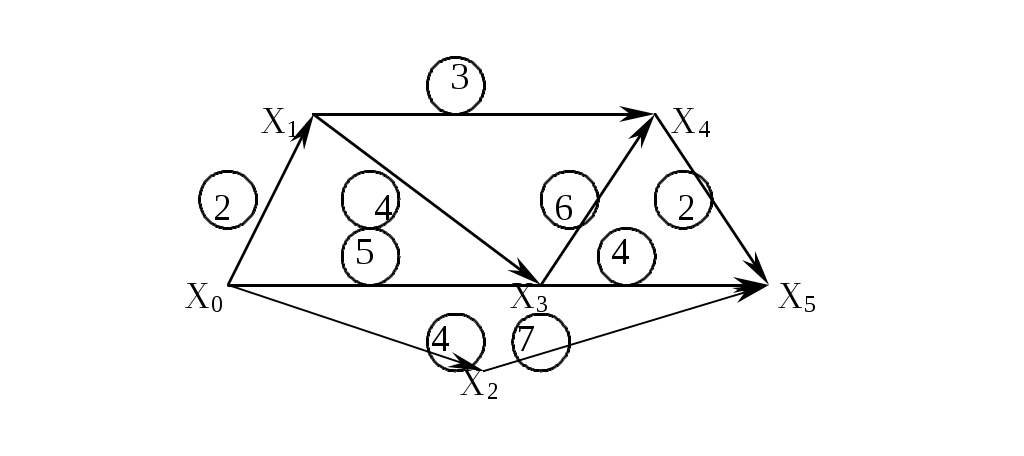 Рис. 3.3.1 Требуется определить путь, по которому из пункта x0 в пункт x5 можно доставить груз в кратчайшие время, и само кратчайшее время доставки. Итак, задача о кратчайшем пути между двумя фиксированными вершинами ориентированного графа предполагает, во-первых, определение длины кратчайшего пути, во-вторых, определение самого кратчайшего пути. Алгоритм Алгоритм решения этой задачи позволяют определить кратчайший путь и его длину за конечное число шагов. Каждая вершина графа получает некоторую числовую метку на первом шаге. Затем метки, вообще говоря, могут меняться, становясь на некотором шаге постоянным числом. Установившаяся метка данной вершины есть кратчайшее расстояние от этой вершины до вершины x0. Если пути, соединяющего x0 и xn, не существует, будем считать длину кратчайшего пути между этими вершинами равной +  . Алгоритм состоит в последовательном выполнении следующих операций: На первом шаге ставим следующие метки: для вершины x0:0=0, для любой другой вершины xi j=+ (i=1,…,n);Ищем на графе такую дугу (xi,xj), для которой j-i>l(xi,xj). Причем разность - считаем равной 0. Если такая дуга найдется, меняем метку вершины xj на  . Если такой дуги не найдется, то пути, соединяющего x0 с xn, не существует, т.к. из x0 ни в какую другую вершину графа не идет ни одна дуга.;Повторяем процедуру пункта 2 до тех пор, пока метки вершин не перестанут меняться. Установившиеся метки обозначим *i (i=1,2,…,n). При этом может быть два случая: *n=+ . Это значит, что пути, соединяющего x0 и xn, не существует. Длина кратчайшего пути равна + . *n – конечное число. Оно равно кратчайшему расстоянию между вершинами x0 и xn. Кратчайший путь получаем следующим образом. Ищем вершину  такую, что  , затем  , для которой  и т.д. до тех пор, пока не придем в вершину  = x0. Путь, проходящий через отмеченные вершины  , является кратчайшим. Как следует из построения и правил изменения меток, метки вершины xi (i=1,…,n) могут меняться конечное число раз (метка вершины x0 0=0 не меняется), т.к. конечная метка всякой вершины равна длине некоторого пути из x0 в данную вершину xi. Из построения следует, что отмеченный путь (  ) – есть кратчайший путь. В самом деле, пусть существует другой путь  из вершины x0 в xn, проходящий через вершины x0, y1, y2, …, yr, xn. Из построения следует, что Складывая эти неравенства и учитывая, что  = 0, получим  , т.е.  . Заметим, что решение задачи может не быть однозначным, т.е. существует несколько путей минимальной длины из вершины x0 в xn. Рассмотренный алгоритм известен в литературе как алгоритм Форда. Решение данной задачи можно ускорить, сократив число шагов, если пользоваться формулой  . (3.3.1)Задача об отыскании кратчайшего пути между двумя вершинами ориентированного графа может быть решена методами целочисленного программирования. Решение по приведенному алгоритму является более простым. Обратимся к приведенному выше примеру. Определим кратчайший путь, соединяющий пункты x0 и x5. При этом будем пользоваться формулой (3.3.1) Для вершины x0 полагаем 0=0. Для всех остальных вершин i=+ (i=1…,5). Затем ищем дугу, для которой j-0>l(x0,xj). Начнем с вершины x1.1-0= >l(x0,x1)=2.Следовательно, меняем метку вершины x1 на ’1=0+l(xo,x1)=2. Аналогично определяем метку вершины X2 ’2=0+l(xo,x2)=4. Чтобы найти изменившуюся метку вершины x3, следует воспользоваться формулой (3.3.1), т.к. в вершину x3 направлены две дуги, идущие из двух разных верши x0 и x1:
Аналогично определяем новые метки для вершин x4 и x5:
В данном случае получили установившиеся метки вершин на втором шаге (на первом шаге полагали 0=0, i=+ ). Каждая из меток ’j – длина кратчайшего пути из вершин xi в данную вершину xj. Длина кратчайшего пути из x0 в x5 есть *5=’5=7. При подсчете значений ’j справа в скобках отмечены вершины, по которым достигается минимум. Так, для x5 ’5=7, если прийти в эту вершину из вершины x4, т.е. ’5=’4+l(x4,x5). Метка для вершины x5 примет большее значение, если прийти в x5 из x2 или x3. Следовательно, кратчайший путь в x5 проходит через вершину x4 (p1=4 в приведенных выше обозначениях). В x4 он идет через вершину x1 (p2=1), в x1 из x0 (p3=р4=0). Итак, кратчайший путь из вершины x0 в x5 проходит через вершины x0,x1,x4,x5. Искомый путь есть (x0,x1,x4,x5); l()=7. В рассмотренном примере установившиеся метки получили за один шаг, потому что, воспользовавшись формулой (3.3.1), определили кратчайший путь между входом и выходом графа-сети. Заметим, что для графов-сетей кратчайший путь между входом и выходом графов всегда существует. Причем он может быть получен за один шаг без предварительного изменения меток, т.е. алгоритм становится совсем простым, если пользоваться формулой (3.3.1) и правильной нумерацией вершин графа, что и было проделано в этой задаче. Сети. Отношение порядка между вершинами ориентированного графа Ориентированный граф без циклов, имеющий одну вершину без входящих дуг (вход графа) и одну вершину без выходящих дуг (выход графа), называется сетью. Отыскание экстремальных путей на графах такого вида используется в различных экономических расчетах. К их числу относятся рассмотренная выше задача, а также задачи сетевого планирования. В любом ориентированном графе без циклов можно установить отношение порядка между его вершинами. Вершина xi предшествует вершине xj,  , если существует дуга из xi в xj. Это отношение порядка удовлетворяет аксиомам порядка:если xi предшествует xj, то xj не предшествует xi; если xi предшествует xj, а xj предшествует xk, то xi предшествует xk. «Правильная» нумерация вершин графа заключается в том, что если xi предшествует xj, то номера i и j должны удовлетворять неравенству i На графе-сети практически это можно сделать, используя распределение вершин по рангам методом вычерчивания дуг. Вычеркиваем дуги, исходящие из входа графа, вершины x0. Вершины, соответствующие концам этих дуг и не имеющие после этой операции входящих дуг, относим к вершинам I-го ранга. На графе G (рис.3.3.1) вершинами I-го ранга являются вершины x1 и x2. Вершины I-го ранга получают первые порядковые номера 1,2. Внутри одного ранга нумерация произвольна. Затем вычеркиваем дуги, выходящие из вершин I-го ранга. Вершины, соответствующие концам таких дуг и не имеющие после этих операций входящих дуг, относим к вершинам 2-го ранга. Они получают следующие порядковые номера. В нашем примере к вершинам 2-го ранга относится одна вершина x3. Процесс вычеркивания дуг продолжается до тех пор, пока все вершины графа не будут занумерованы. Последний порядковый номер получит вершина xn – выход графа. В рассмотренном примере все вершины распределены по 4 рангам. К вершинам 3-го ранга принадлежит x4, а к вершинам 4-го ранга – x5. Существуют и другие способы «правильной» нумерации вершин графа, в том числе алгоритм Форда для нумерации вершин графа. Задача о пути максимальной длины между двумя вершинами ориентированного графа в сетевом планировании Постановка задачи Задача ставится следующим образом. Задан конечный ориентированный граф без контуров G(x,u). Каждой дуге графа «u» ставится в соответствие длина дуги l(u). Требуется определить длиннейший путь, соединяющий две вершины графа x0 и xn. Аналогичные задачи можно ставить для ориентированных графов с контурами, а также неориентированных графов. Но в этом случае во избежание бессодержательности задачи нужно вводить дополнительные условия, исключающие пути бесконечной длины. Решение задачи состоит как в отыскании пути максимальной длинны между двумя фиксированными вершинами графа, так и в определении величины этого пути. Одну из основных задач сетевого планирования составляет отыскание путей максимальной длины между входом и выходом графа-сети. Алгоритм Каждая вершина графа получает числовую метку, которая может меняться конечное число раз. Установившаяся метка – величина длиннейшего пути из вершины x0 в данную вершину xj. В частности, установившаяся метка вершины xn есть величина длиннейшего пути из x0 в xn. Чтобы определить искомый путь, нужно рассмотреть последовательность шагов, на каждом из которых ищется одна из дуг длиннейшего пути между x0 и xn. Алгоритм состоит в последовательном проведении следующих этапов: Полагаем λ0 = 0; λi = -∞ (i = 1,…,n). Ищем дугу (xi, xj) такую, что  . Если такой дуги нет, то не существует пути, соединяющего x0 и xn. Если такая дуга найдется, то изменяем метку j на ’j=j + + l(x0,xj). Продолжаем процедуру пункта 2 до тех пор, пока метки вершин xi не перестанут меняться. Установившиеся метки обозначим *i. При этом могут встретиться два случая: *n= - , это соответствует тому, что пути, соединяющего вершины x0 и xn, не существует;*n- конечное число. Оно равно длине пути максимальной длины из x0 в xn. Сам путь находим, отмечая вершины, по которым достигается максимум, т.е. те вершины, для которых  .Если между вершинами графа-сети установлено отношение порядка, т.е. они «правильно» занумерованы, то решение задачи можно получить за один шаг, произведя подсчет меток с учетом следующей формулы:  . (3.3.2)Пример. Определим длиннейший путь на графе, изображенном на рис.3.3.1, а также его длину. Вначале полагаем для вершины x0 0=0 и j=- для вершин xi (i=1,…,5).Затем, т.к. 1-0=- <l(x0,x1), меняем метку вершины x1, т.е. 1, на
Аналогично ’2=0+l(x0,x2)=4. Чтобы найти метку вершины x3, пользуясь формулой (3.3.2)
Справа в скобках отмечаем вершины, по которым достигается максимум длины. Аналогично
Искомый путь имеет длину l()=*5=14. Причем в x5 он идет из вершины x4, в x4 из x3, в x3 из x1, в x1 из x0: x5,x4,x3,x1,x0. Следовательно, =(x0,x1,x3,x4,x5). Путь максимальной длины называют критическим путем. Следовательно, критический путь в рассмотренном примере есть =(x0,x1,x3,x4,x5), а его длина l()=14. |