Мера Жордана. Измеримые множества. Примеры измеримых и неизмеримых множеств
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
|
Приветики))))
ОглавлениеПонятие меры 2 Определение меры множества 3 Если говорят m(A) = 0 это значит 3 Свойства множеств с мерой 0 4 Критерий измеримости 4 Свойства измеримых множеств 6 Понятие мерыДано 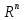 , в нём рассматриваем прямоугольник (это такое множество точек) , в нём рассматриваем прямоугольник (это такое множество точек)П= 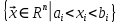 В случае 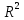 это обычный прямоугольник, для это обычный прямоугольник, для 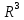 это куб, для R это отрезок. это куб, для R это отрезок. Мера обозначается 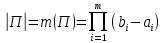 (произведение длин всех сторон) В двумерном пространстве отрезокможно считать прямоугольником, но у него будет мера = 0 Фигурой 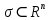 будем называть множество будем называть множество 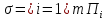 конечное объединение прямоугольников, которые пересекаются только по границам конечное объединение прямоугольников, которые пересекаются только по границамВозьмём фигуру и разобъём её  или вот так вот или вот так вот  (по пунктиру) (по пунктиру)Любую фигуру можно представить как объединение конечного числа разбиений фигуры на прямоугольники (бесконечным числом способов) Сумма мер прямоугольников всегда будет одна 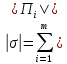 Определение меры множестваA – ограниченное множество, 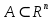 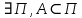 (ограниченное <–> найдётся прямоугольник в котором содержится А) (ограниченное <–> найдётся прямоугольник в котором содержится А)Обозначим следующие фигуры: 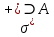 (фигура содержит А) (фигура содержит А)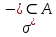 (фигура содержится в А) (фигура содержится в А)Тогда 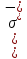 - мера фигуры - мера фигуры 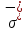 ограничена сверху мерой прямоугольника ограничена сверху мерой прямоугольника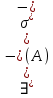 – найдётся супремум внутренних мер фигуры – называется внутренней мерой множества А Аналогично 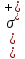 – мера фигуры – мера фигуры 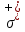 ограничена снизу нулём ограничена снизу нулём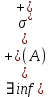 – найдётся инфинум внешних мер фигуры – внешняя мера множества А – найдётся инфинум внешних мер фигуры – внешняя мера множества АЕсли 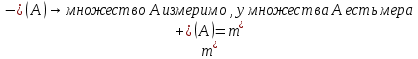 Собственно его мера 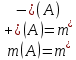 Если говорят m(A) = 0 это значит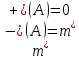 Что значит 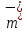 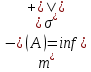 =0 =0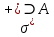 Супремум равен нулю – значит, что если мы возьмём, отступим от нуля вправо, то всегда найдётся данная фигура 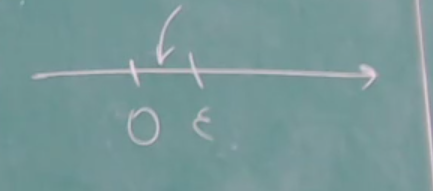 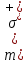 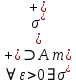 Вот что значит мера множества равна нулю Свойства множеств с мерой 0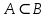 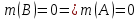 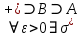 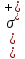 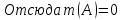 A, B измеримые 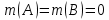 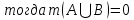 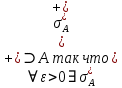 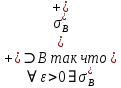 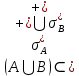 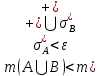  Критерий измеримостиМножество измеримо только тогда, когда мера его границы равна нулю. 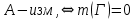 доказательство доказательство 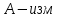 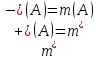 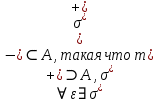 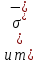   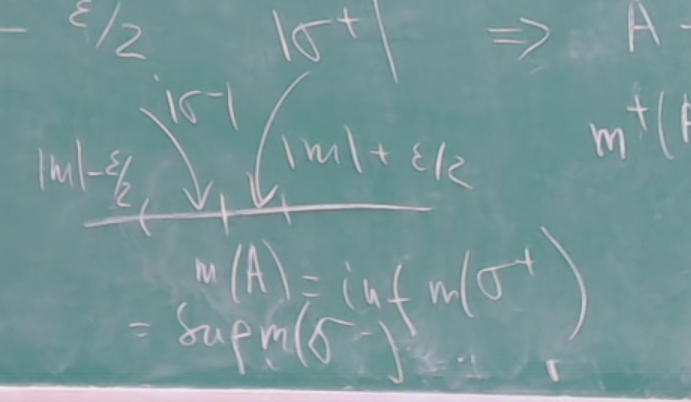 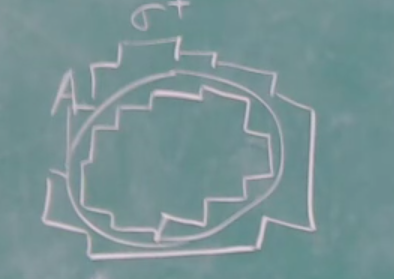 Рассмотрим 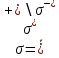 (разность фигур) (разность фигур)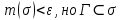 Это означает, что мера границы равна нулю В обратную сторону 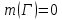 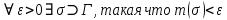 Тогда обозначим фигурами: 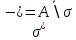 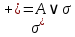 Тогда 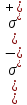 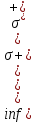 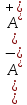 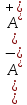 Свойства измеримых множествЕсли 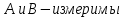 , то , то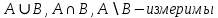 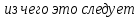 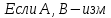 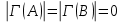 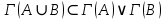 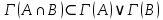 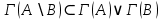 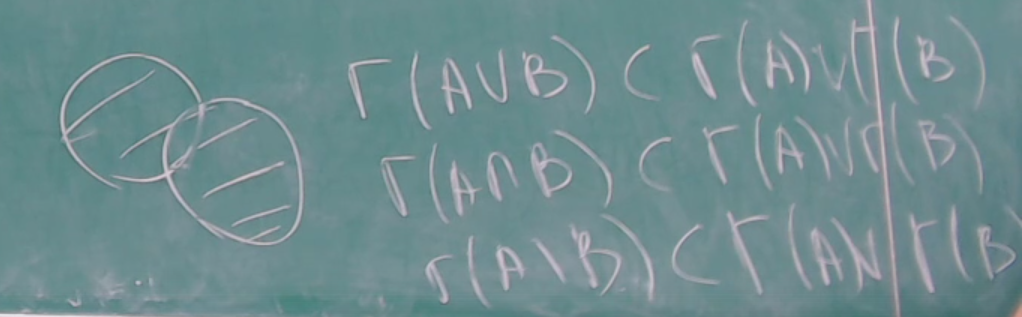 Мера/площадь непрерывной дуги кривой, однозначно проектируемой на какую-то прямую, равна нулю. Вот есть у нас кривая, которая проектируется на прямую (ОХ). 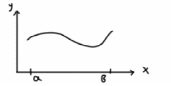 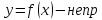 Мы доказывали, когда криволинейная трапеция имеет площадь (???) Чем является кривая для трапеции? Она является частью границы 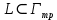 Трапеция имеет площадь – измерима 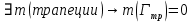 Значит и мера дуги равна нулю |
