ОТЧЕТ ПО МО. Методы оптимизации
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра безопасности информационных систем (БИС) Отчет по дисциплине «Методы оптимизации» Выполнил студент гр. 731-2 А.С.Батаев Принял Старший преподаватель кафедры КИБЭВС А.Ю.Якимук Томск 2022 1 ВведениеЦелью работы является ознакомление с методами минимизации одномерных и многомерных функций. 2. Ход работыМинимизация одномерной функции без ограничений на переменную Код для минимизации одномерной функции без ограничений представлен в приложении А. Для минимизации одномерной функции используются методы: Фибоначчи, дихотомии и золотого сечения. Метод Фибоначчи подразумевает под собой использование последовательность чисел Фибоначчи вместе с итерационными формулами для получения определенной промежуточной точки, расположенной в середине определенного отрезка. Далее отрезок уменьшается и выполняются последующие циклические итерации пока не будет достигнуто условие останова. Метод дихотомии подразумевает под собой вычисление значений функции на определенном отрезке с помощью точек, полученных специальным соотношением. Далее происходит сравнение результатов и сокращение отрезка и повторяется вышеописанный алгоритм, пока не будет достигнуто условие останова. Метод золотого сечения подразумевает под собой вычисление значений функции на определенном отрезке, последующем сравнении значений и сокращении отрезка пропорциональным отношению чисел 0,382 и 0,612. Начальный отрезок задается большим, длиной не менее 10 и не симметричным. Условие останова было выбрано равным 0,001. Минимизация одномерной функции f1(x)Функция f1(x) задана формулой f1(x) = 2*(x - 7) * (x - 5) * (x -2). График функции представлен на рисунке 2.1. 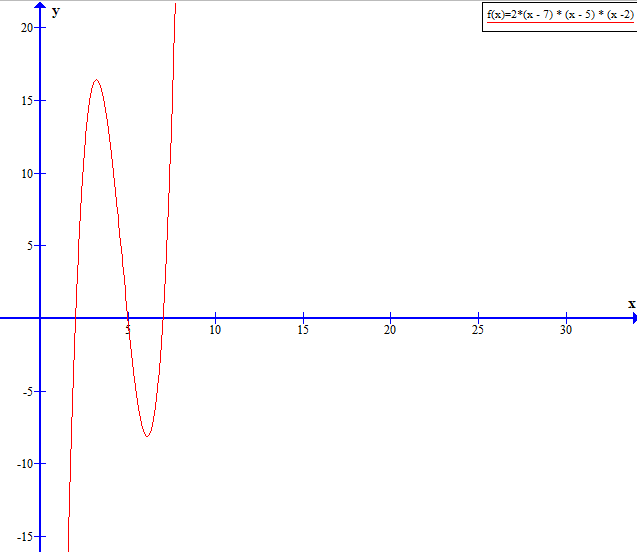 Рисунок 2.1 – График функции f1(x) Результат работы программы представлен на рисунке 2.2-2.4. 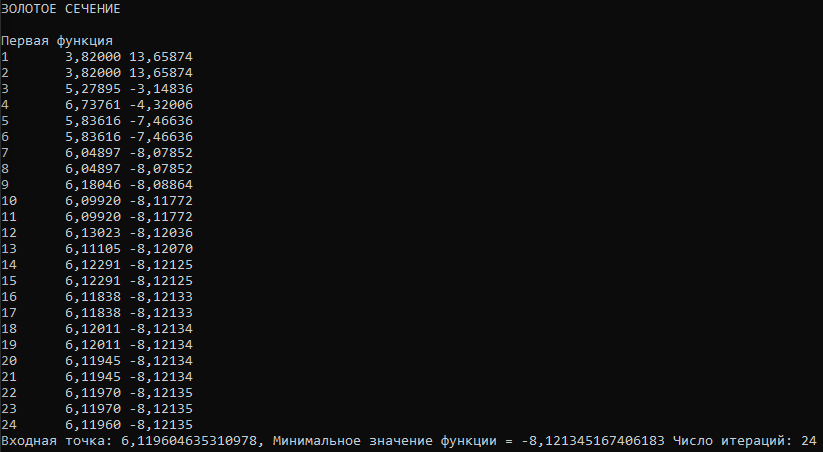 Рисунок 2.2 – Результат работы программы для функции f1(x) методом Золотого сечения 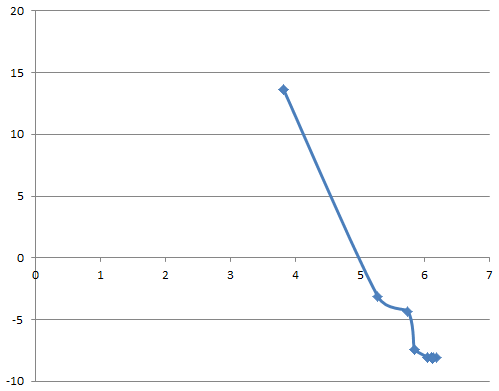 Рисунок 2.3 – График работы программы для функции f1(x) методом Золотого сечения 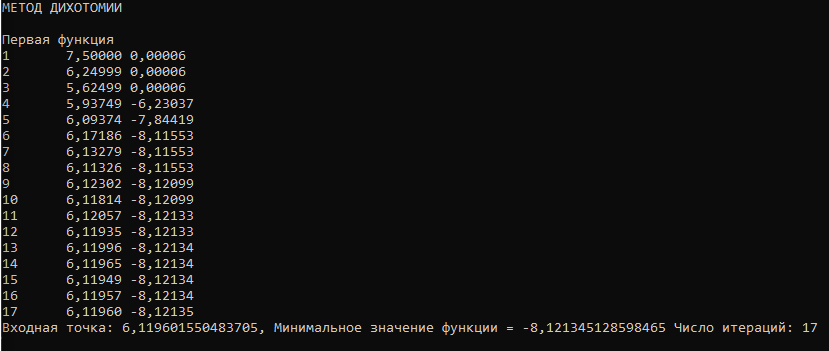 Рисунок 2.4 – Результат работы программы для функции f1(x) методом Дихотомии 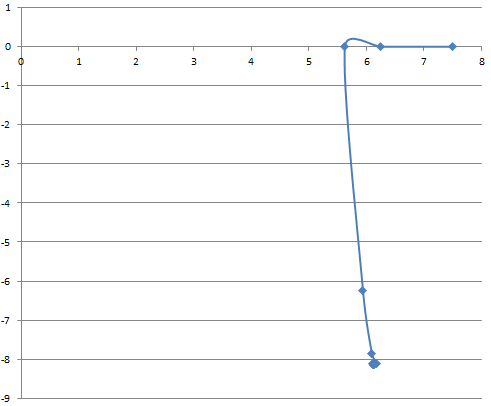 Рисунок 2.5 – График работы программы для функции f1(x) методом Дихотомии  Рисунок 2.6 – Результат работы программы для функции f1(x) методом Фибоначчи 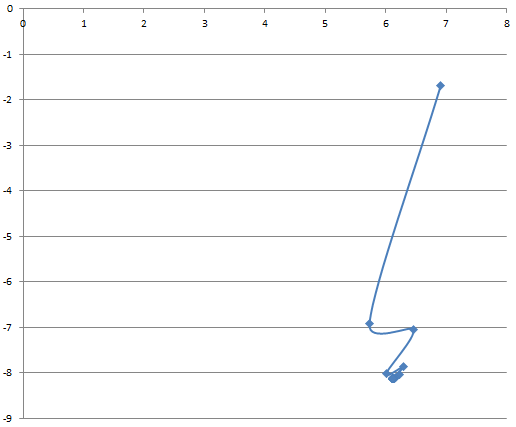 Рисунок 2.7 – График работы программы для функции f1(x) методом Фибоначчи |
