КП_ОТН_18_21_вариант_Канарев. Методы расчета показателей надежности сжат
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
3. Методы расчета показателей надежности СЖАТ3.1 Статистические оценки показателей надежности3.1.1 Построение функции распределения и функции плотности распределения по статистической выборке На основании статистической выборки из 30 значений построить гистограмму частот. Используя критерий Пирсона, убедиться в экспоненциальном законе распределения времени наработки до отказа t. Построить теоретическую функцию плотности распределения a(t).
Переведем время наработки до отказа в часы, в результате статистика примет следующий вид (таблица 1.1). (*24) Таблица 1.1
Статистический ряд для данной выборки, а также номер интервала, в который попадает определенное значение представлены в таблице 2. Таблица 2
Возьмем диапазон значений случайной величины от 360 до 141288. Диапазон значений случайной величины t: 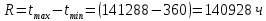 Количество интервалов K: 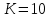 Интервал 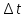  Частота попадания в i-й интервал 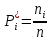 1. 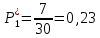 2. 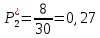 3. 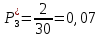 4. 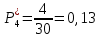 5. 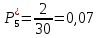 6. 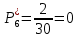 ,07 ,077. 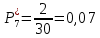 8. 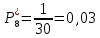 9. 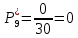 10. 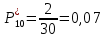 Статистическая плотность вероятности времени безотказной работы (частота отказов 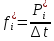 1. 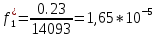 2. 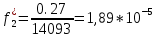 3. 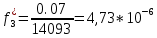 4. 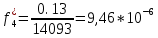 5. 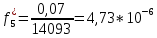 6. 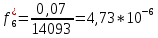 7. 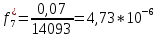 8. 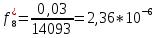 9. 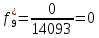 10. 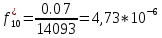 Таблица 3
Построим полигон и гистограмму частот. 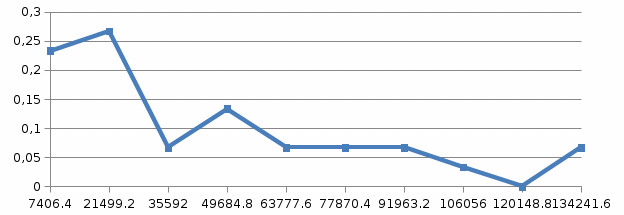 Рис. 1 График полигона (частота попадания в заданный интервал) 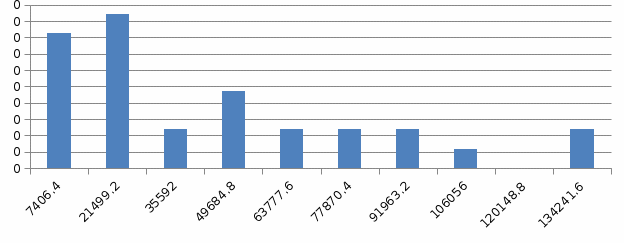 Рис. 2. Гистограмма (статистическая плотность распределения) Построим статистическую функцию распределения Q. 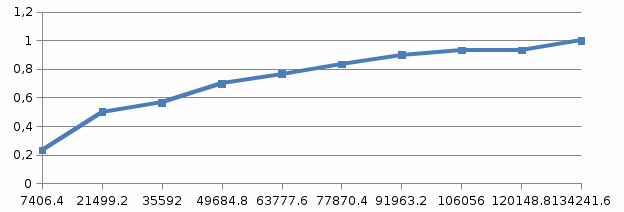 Рис. 3. Статистическая функция распределения По виду гистограмм можно предположить экспоненциальный закон распределения времени наработки t. Примем эту гипотезу и проверим степень ее правдоподобия, используя критерий Пирсона. Для этого построим теоретическую функцию частоты отказов, предполагая экспоненциальный закон распределения для времени наработки: 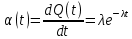 для значений ti –центров интервалов для значений ti –центров интервалов 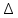 ti, i=1,2,3,4,5 и ti, i=1,2,3,4,5 и 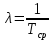 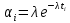 1. 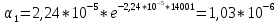 2. 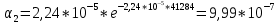 3. 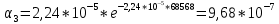 4. 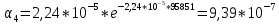 5. 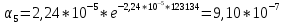 6. 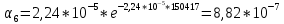 7. 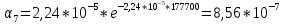 8. 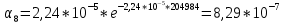 9. 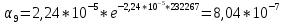 10. 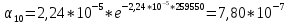 Среднее время наработки до отказа 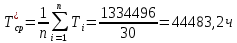 Интенсивность отказов 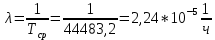 Теоретическое число попаданий в i-ый интервал: 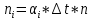 1. 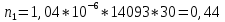 2. 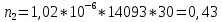 3. 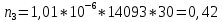 4. 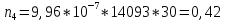 5. 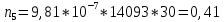 6. 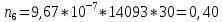 7. 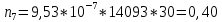 8. 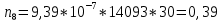 9. 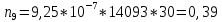 10. 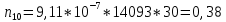 Найдем значения 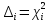 – меры расхождения между теоретическими числами – меры расхождения между теоретическими числами 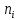 и экспериментальными и экспериментальными 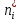 : :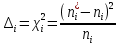
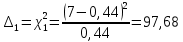 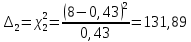 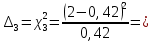 5,78 5,78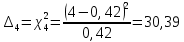 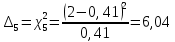 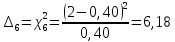 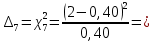 6,32 6,32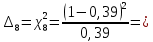 0,91 0,91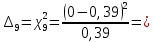 0,39 0,39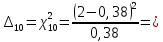 6,76 6,76Просуммировав значения этого ряда, найдем значение 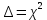 : :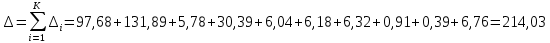 Число степеней свободы 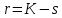 =10-1=9 =10-1=9Для r=9 и 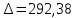 находим вероятность γ≤0,01. Это значение не превышает порог γ=0,3, что говорит о несогласии экспериментальных данных с гипотезой об экспоненциальном законе распределения времени наработки до отказа. находим вероятность γ≤0,01. Это значение не превышает порог γ=0,3, что говорит о несогласии экспериментальных данных с гипотезой об экспоненциальном законе распределения времени наработки до отказа.3.1.2 Статистическая оценка параметров надежности восстанавливаемых устройств На предприятии в момент времени t0=0 было установлено N0 восстанавливаемых устройств. При проверках на промежутках времени 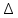 ti(i+1) (i=0,1,2) подсчитывалось, сколько устройств отказало на данном промежутке ni(i+1) и сколько было восстановлено nвi(i+1). (табл. 5) ti(i+1) (i=0,1,2) подсчитывалось, сколько устройств отказало на данном промежутке ni(i+1) и сколько было восстановлено nвi(i+1). (табл. 5) Таблица 5
Найти статистические параметры безотказности и ремонтопригодности на промежутке времени 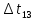  Статистические оценки параметров безотказности Вероятность безотказной работы 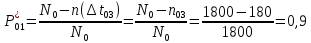 Вероятность отказа 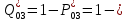 0,9=0,1 0,9=0,1Частота отказов 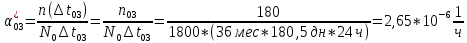 Интенсивность отказов 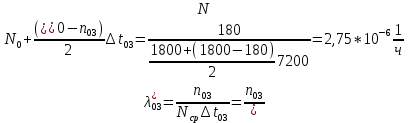 Параметр потока отказов 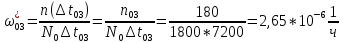 Статистические оценки параметров ремонтопригодности Вероятность восстановления 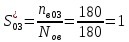 Считаем, что число поставленных на восстановление устройств на начало промежутка 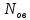 ,равно числу неисправных устройств на всем рассматриваемом промежутке. ,равно числу неисправных устройств на всем рассматриваемом промежутке.Частота восстановления 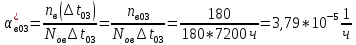 Интенсивность восстановления 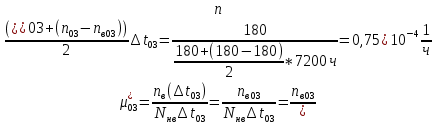 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

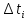 , ч
, ч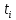 , ч
, ч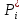
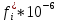 , 1/ч
, 1/ч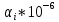 , 1/ч
, 1/ч