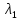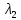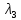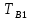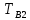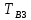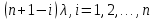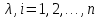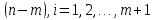КП_ОТН_18_21_вариант_Канарев. Методы расчета показателей надежности сжат
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессовИсходные данные Вариант № 18 λik=λ=18*10-4 1/ч. μik=μ=0,55 1/ч. РАСЧЕТЫ 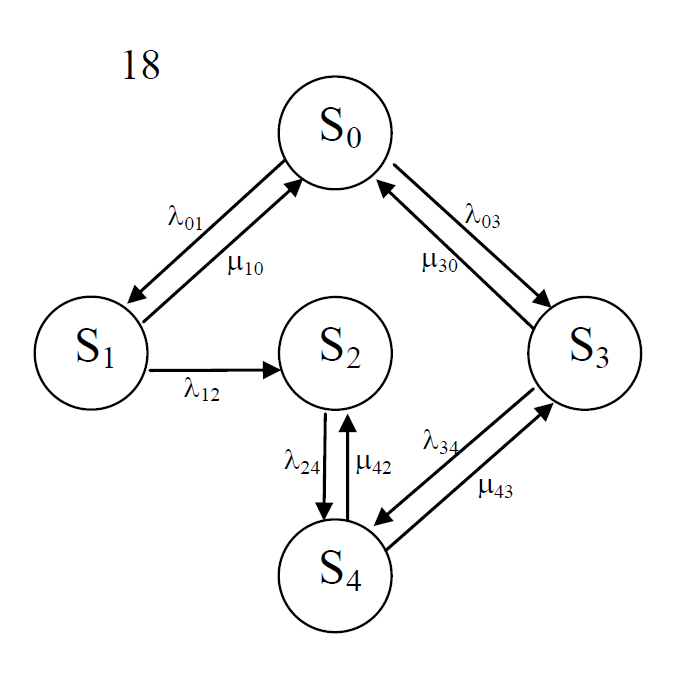 Рисунок 5. Граф состояний схемы. Исходя из графа, система может находиться в одном из четырех состояний: 0 – исправное состояние; 1 – первое работоспособное состояние, отказал первый элемент, второй и третий – исправны; 2 – второе работоспособное состояние, отказал второй элемент, первый и третий – исправны; 3 – третье работоспособное состояние, отказал третий, первый и второй – исправны; 4 – неработоспособное состояние, отказали последовательно три элемента и находятся в состоянии ремонта. Составим систему уравнений Колмогорова для финальных вероятностей нахождения во всех состояниях.    Система состоит из шести уравнений, пять неизвестных, значит можно путем подстановки выразить каждую переменную: Р0=0,355 P1=0,131 P2=0,487 P3=0,025 P4=0,002 Вероятность отказа системы: QC=P4=0,00018 Вероятность безотказной работы: PC=1-QC=1-0,00018=0,99982 Время наработки на отказ: Tср= 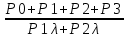 = =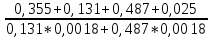 =897,1 ч. =897,1 ч.Интенсивность отказов: λc=1/ Tср=1/897,1 = 0,00111 1/ч. Среднее время восстановления: Tв= 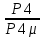 = =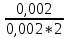 =0,5 =0,5Коэффициент готовности: Кг= 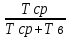 = =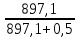 =0,999 =0,999Для нахождения среднего времени безотказной работы выполним преобразование Лапласа для уравнений Колмогорова с учетом начальных условий: 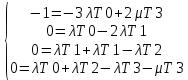 → → 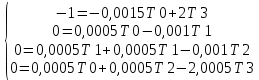 Система состоит из четырех уравнений, 3 неизвестных, значит можно путем подстановки выразить каждую переменную: T0=1333 ч. T1=666 ч. T2=666 ч. T3=0,5 ч. Среднее время безотказной работы системы: Tот=T0+T1+T2+T3=1333+666+666+0,5=2665,5 ч. 3.4 Структурный метод расчета надежности Исходные данные Вариант № 10 1 Узел: (n1*n2) v (n3*(n4 v n5)) 2 Узел: n6 3 Узел: n7 v n8 v n9 λ1=18*10-51/ч. λ2=18*10-51/ч. λ3=18*10-51/ч. λ4=18*10-51/ч. λ5=18*10-51/ч. λ6=18*10-51/ч. λ7=18*10-51/ч. λ8=18*10-51/ч. λ9=18*10-51/ч. Тву1= 18 ч. Тву2= 18 ч. Тву3=18 ч. t =1 год = 8760 ч РАСЧЕТЫ Логическая функция схемы:  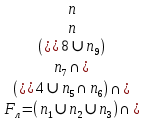 Арифметическая функция: 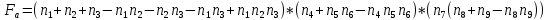 Преобразуем узлы схемы:  Рис.8. 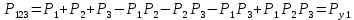 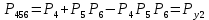 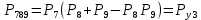 Функция надежности: 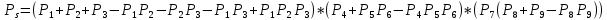 Значения функции надёжности схемы за t=1 год (8760 ч): 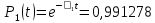 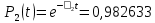 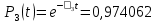 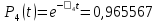 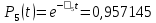 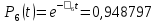 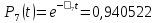 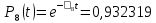 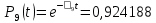 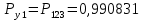 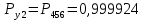 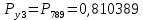 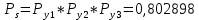 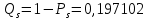 Интенсивностьотказов: 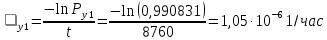 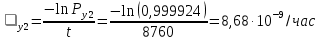 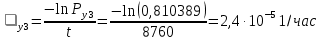 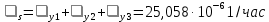 Среднее время наработки до отказа: 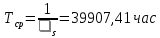 Среднее время восстановления системы: 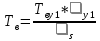 + +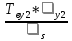 + +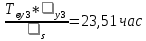 Коэффициент готовности: 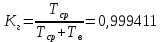 Вывод: после определения всех параметров системы можно сделать вывод, что система в течении года будет работать надёжно с вероятностью 80,2898% 3.5 Топологический метод расчета надежности резервированных систем На рис. 1 приведена структурная схема некоторой системы с восстановлением. Значения интенсивности отказа и времени восстановления каждого элемента, вид и кратность резервирования, а также число ремонтных бригад заданы в соответствии с вариантом (табл.1). 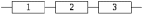 Рис. 1. Структурная схема системы Необходимо построить систему с резервированием и найти выигрыш надёжности по времени наработки на отказ: 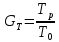 , где , где 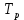 - время наработки на отказ для резервированной системы, - время наработки на отказ для резервированной системы, 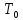 - время наработки на отказ для нерезервированной системы. - время наработки на отказ для нерезервированной системы.Исходные данные приведены в табл. 1. Таблица 1
Таблица 2 Интенсивность переходов 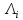 в зависимости от вида резервирования в зависимости от вида резервирования
Структурная схема системы после резервирования приведена на рис.2.  Рис. 2. Структурная схема после резервирования Время наработки на отказ системы без резервирования: 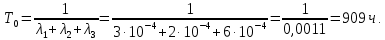 Интенсивность отказа 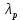 и интенсивность восстановления и интенсивность восстановления 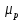 . .Если все элементы системы идентичны по безотказности и ремонтопригодности, то функционирование систем с постоянно включённым резервом, резервом замещением, с мажоритарным резервированием и скользящим резервом, обслуживаемых любым количеством ремонтных бригад, будет описываться графом, показанным на рис. 3.  Рис. 3. Граф состояний резервированной системы с идентичными элементами Приняты следующие обозначения: 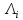 – интенсивности переходов, соответствующие отказам элементов системы, – интенсивности переходов, соответствующие отказам элементов системы, 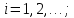 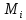 – интенсивности переходов, соответствующие восстановлениям элементов системы. – интенсивности переходов, соответствующие восстановлениям элементов системы.Воспользуемся таблицей 2 и приведёнными ниже формулами: наработка на отказ: 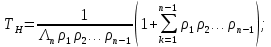 где 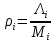 среднее время восстановления: 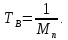 интенсивность восстановления 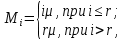 где r – число ремонтных бригад. Интенсивность отказа первой системы после резервирования определяется по формуле в соответствии с таблицей 2 для постоянного резервирования: Найдем интенсивность отказа и интенсивность восстановления первого элемента после резервирования 𝝀1р и μ1р. 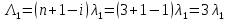 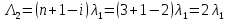 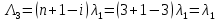 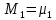 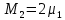 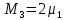 где 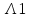 , ,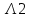 , , 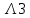 , M1, M2, M3 – интенсивности переходов для представленного на рисунке 3 графа. , M1, M2, M3 – интенсивности переходов для представленного на рисунке 3 графа.Используя формулы, находим наработку на отказ резервированного элемента 1: 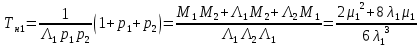 Учитывая экспоненциальный закон распределения интенсивностей переходов, найдем интенсивность отказа дублированного элемента 1. 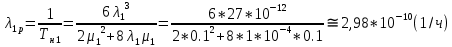 Интенсивность восстановления резервированного элемента 1. 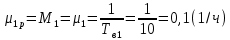 Аналогично найдем интенсивность отказа и интенсивность восстановления для резервированного (дублированного) элемента 2. 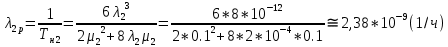 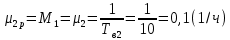 Найдем интенсивность отказа и интенсивность восстановления третьего элемента после резервирования 𝝀3р и μ3р, для этого воспользуемся формулами и таблицей 1. Используя данные таблицы 1 для резервирования замещением с кратностью 2 (1 – основной и 2 – резервных), получим: 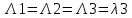 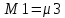 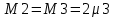 где 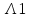 , ,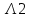 , , 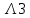 , M1, M2, M3 – интенсивности переходов для представленного на рисунке 3 графа. , M1, M2, M3 – интенсивности переходов для представленного на рисунке 3 графа.Используя формулы, находим наработку на отказ резервированного элемента 1: 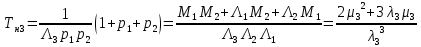 Учитывая экспоненциальный закон распределения интенсивностей переходов, найдем интенсивность отказа дублированного элемента 3. 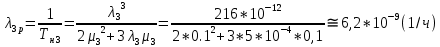 Интенсивность восстановления резервированного элемента 3. 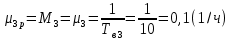 4. Время наработки на отказ системы с резервированием 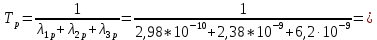 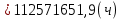 5. Выигрыш надёжности по времени наработки на отказ 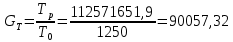 | ||||||||||||||||||||||||||||||||||||||||||||||