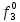КП_ОТН_18_21_вариант_Канарев. Методы расчета показателей надежности сжат
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
3.2 Расчет надежности комбинационных схемИсходные данные Вариант № 18 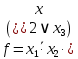 p1 = 0,7 p2 = 0,2 p3 = 0,6 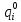 = 0,001 = 0,001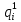 = 0,001 = 0,001Расчет надежности комбинационных схем Комбинационная схема – это логическая схема, состояния выходов которой однозначно зависят от состояния входов. Построим комбинационную схему на двухвходовых логических элементах по заданной функции алгебры логики. 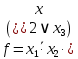 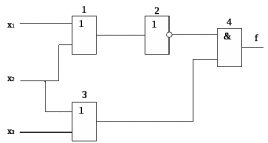 Рисунок 4. Комбинационная схема на двухвходовых логических элементах Таблица 4. Таблица истинности.
Таблица 5. Функции, реализуемые схемой при неисправности.
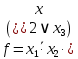 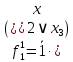 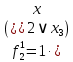 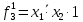 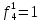 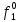 = = 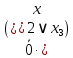  = = 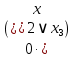 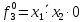 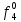 = =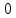 Функция ошибки 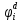 называется функция, принимающая значение “1” на тех и только на тех входных наборах, на которых функция, реализуемая исправной схемой – f, и функция, реализуемая неисправной схемой - fi, принимают различные значения. называется функция, принимающая значение “1” на тех и только на тех входных наборах, на которых функция, реализуемая исправной схемой – f, и функция, реализуемая неисправной схемой - fi, принимают различные значения.Неисправность ni называется существенной, если на входном наборе Si 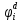 = f * = f * 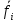 v v 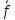 * fi, то есть если * fi, то есть если 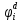 =1 то неисправность для данного набора является существенной. =1 то неисправность для данного набора является существенной.Таблица 6. Функции ошибки.
Функция ошибки в десятичном виде: 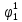 = {1} = {1}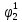 = {2,3,5,6,7} = {2,3,5,6,7}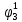 = {0,2,3,4,5,6,7} = {0,2,3,4,5,6,7}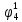 = {0,2,3,4,5,6,7} = {0,2,3,4,5,6,7}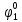 = {2,3,5,6,7} = {2,3,5,6,7}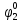 = {0,2,3,4,5,6,7} = {0,2,3,4,5,6,7}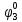 = {0,2,3,4,5,6,7} = {0,2,3,4,5,6,7}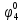 = {0,2,3,4,5,6,7} = {0,2,3,4,5,6,7}Функция ошибки в алгебраическом выражении: 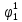 = =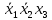 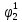 = = 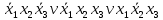 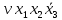 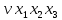 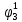 = = 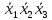 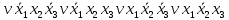 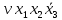 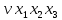 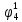 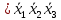 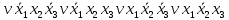 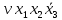 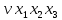 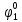 = = 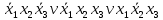 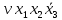 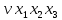 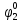 = = 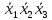 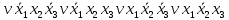 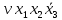 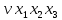 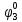 = = 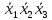 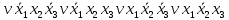 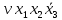 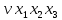 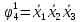 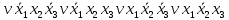 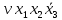 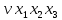 p1, p2 и p3 – вероятности, того что в момент времени t входная переменная xj=1, соответственно (1- pj) – вероятность того, что xj=0. p1 = 0,7, p2 = 0,2, p3 = 0,6. Таблица7. Вероятность появления входных наборов.
Pf = ∑Rkf Pf = R0 + R1 +R5 + R6 + R7 Pf =0,084+0,336+0,224+0,024+0,096=0,764 Определим вероятность функции ошибки как сумму вероятностей, того, что на выходе схемы происходит ошибка при наличии сбоя: P( 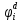 ) = ∑Rkf ) = ∑RkfP( 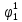 ) = R1= 0,336 ) = R1= 0,336 P( 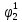 ) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504 ) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504P( 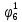 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644P( 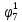 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644P( 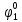 ) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504 ) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504P( 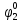 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644P( 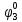 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644P( 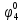 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644Вероятность того, что произойдет неисправность, которая приведет к ошибке на выходе схемы: 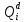 = = 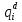 * P( * P(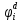 ) )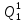 = =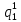 *P( *P(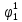 ) = 0,001*0,336=33,6*10-5 ) = 0,001*0,336=33,6*10-5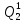 = =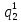 *P( *P(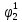 ) = 0,001*0,504=50,4*10-5 ) = 0,001*0,504=50,4*10-5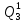 = =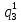 *P( *P(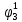 ) = 0,001*0,644 =64,4*10-5 ) = 0,001*0,644 =64,4*10-5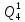 = =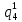 *P( *P(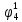 ) = 0,001*0,644=64,4*10-5 ) = 0,001*0,644=64,4*10-5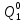 = =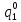 *P( *P(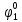 ) = 0,001*0,504=50,4*10-5 ) = 0,001*0,504=50,4*10-5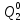 = =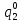 *P( *P(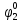 ) =0,001*0,644=64,4*10-5 ) =0,001*0,644=64,4*10-5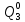 = =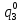 *P( *P(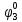 ) = 0,001*0,644=64,4*10-5 ) = 0,001*0,644=64,4*10-5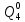 = =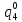 *P( *P(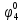 ) = 0,001*0,644=64,4*10-5 ) = 0,001*0,644=64,4*10-5Вероятность ошибки на выходе схемы в момент времени t определяется по следующей формуле: Q = ∑ 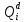 Q = 45,6*10-4 Вероятность отсутствия ошибки на выходе схемы, то есть вероятность исправной работы равна: P = 1-Q = 1 – 45,6*10-4 = 0,99544 В разделе по заданной функции алгебры логики была построена комбинационная схема, после чего была рассчитана ее надежность. Вероятность ошибки на выходе схемы в момент времени t равна 45,6*10-4, вероятность исправной работы схемы - 0,99544. |