Численные методы. 1 Лаборторная работа ЧМ. Методы решения нелинейных уравнений
 Скачать 281.48 Kb. Скачать 281.48 Kb.
|
|
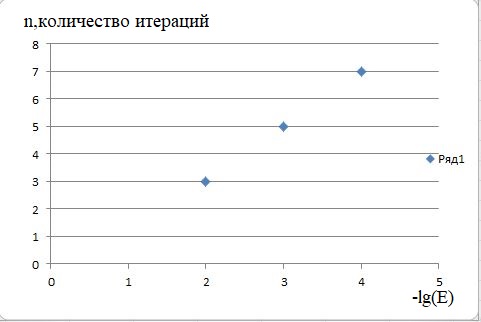
Федеральное агентство связи Ордена Трудового Красного Знамени федеральное бюджетное образовательное учреждение высшего образования «Московский Технический Университет Связи и Информатики» (МТУСИ) Кафедра Информатики Предмет: Вычислительные модели Лабораторная работа № 1 Тема: «Методы решения нелинейных уравнений»Вариант 00 Выполнил: Проверил(а): Величайший преподаватель _________________ Москва 0000 1 Задание 1. Выбрать индивидуальное задание по указанию преподавателя из табл. 1.2-1: · нелинейное уравнение; · метод решения нелинейного уравнения для «ручного расчета»; · метод решения нелинейного уравнения для «расчета на ПК». 2. Отделить корни уравнения. 3. Провести исследование нелинейного уравнения для его решения. · проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости; · выбрать начальное приближение; · сформулировать условия окончания этапа уточнения корня. 4. Провести «ручной расчет» трех итераций. 5. Оценить погрешность результата «ручного расчета». 6. Составить схему алгоритма, написать программу для решения нелинейных уравнений для «расчета на ПК» и провести контрольное тестирование программы, воспользовавшись исходными данными и результатами примера из п.п.1.2-1.5. 7. Решить нелинейное уравнение с точностью , воспользовавшись написанной программой для «расчета на ПК». 8. Построить зависимость числа итераций от заданной точности –n(E). 1.Индивидуальное задание: (уравнение, методы решения). 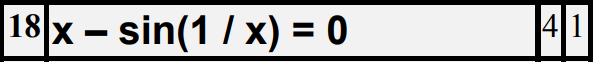 t4– хорд ,p1-половинное деление t – номер метода для «расчета на ПК»; p– номер метода для «ручного расчета». Номера методов: 1 – половинное деление;2 – итерации;3 – Ньютона; 4 – хорд. 2 Отделение корней. Произведем отделение корней при помощи программы MathCad 15. 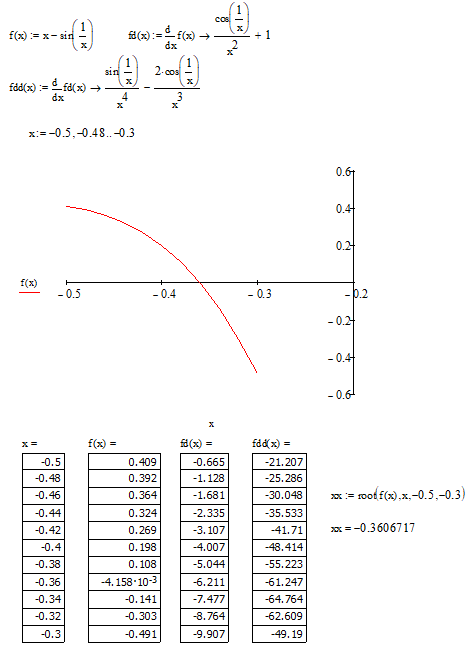 На интервале [-0,5;-0,3] функция имеет один корень, поэтому мы можем использовать этот интервал для расчётов и в этом случае f’(x) и f”(x) непрерывны и знакопостоянны и f(-0,5)*f(-0,3)<0 3 Ручной расчёт. 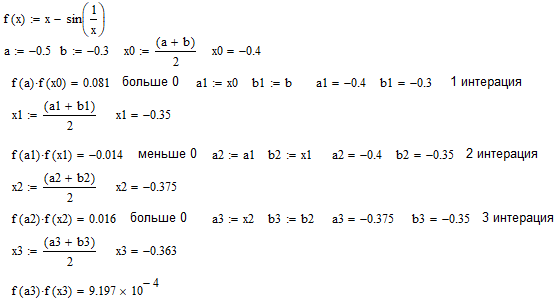 Произведем ручной расчёт методами половинного деления, итераций и Ньютона при помощи программы Microsoft Excel.  Погрешность после 3 итераций равно 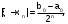 Правая часть этой формулы в нашем случае будет равна 0.025 Исходя из этого, можно утверждать, что корень уравнения X после трех итераций методом половинного деления лежит в промежутке -0,3625±0.025 4 Расчёт на ПК.4.1 Программный код. Option Strict On Option Explicit On Imports System.Math Public Class Form1 Sub vvod(ByRef x As Double, ByVal t As TextBox) x = Val(t.Text) End Sub Sub vivod(ByVal x As Double, ByRef t As TextBox) t.Text = CStr(x) End Sub Sub vivodint(ByRef x As Integer, ByVal t As TextBox) t.Text = CStr(x) End Sub Function f(ByVal x As Double) As Double 'наша функция f(x)=x-sin(1/x) Dim fx As Double fx = x - Sin(1 / x) Return fx End Function Sub Hord_Iteraci(ByVal a As Double, ByVal b As Double,_ ByVal ee As Double, ByRef xn As Double, ByRef fnx As Double, ByRef n As Integer, ByRef lb As ListBox) Dim x, fx, l As Double Dim s As String = "" s = "N" + Space(18) + "x" + Space(27) + "f(x)" +_ Space(18) + "E,погрешность" + vbNewLine lb.Items.Add(s) xn = a 'подвижная точка x = b 'неподвижная точка fx = f(x) 'Значение f(b) fnx = f(xn) 'Значение f(a) Do l = xn 'x(n) n = n + 1 xn = xn - (fnx / (fx - fnx)) * (x - xn) 'x(n+1) fnx = f(xn) 'f(x(n+1) s = Format(n, "00") + Space(10) + Format(xn,_ "0.000000") + Space(14) + Format(fnx, "0.000000") +_ Space(14) + Format(Abs(xn - l), "0.000000") + vbNewLine lb.Items.Add(s) Loop Until Abs(xn - l) < ee End Sub Private Sub Button1_Click(sender As System.Object, e As_ System.EventArgs) Handles Button1.Click Dim a, b As Double 'границы отрезка Dim ee, xn, fnx As Double Dim n As Integer = 0 ListBox1.Items.Clear() vvod(a, TextBox1) 'подвижная точка "в нашем случае это а" vvod(b, TextBox2) 'неподвижная точка "в нашем случае это b" vvod(ee, TextBox3) ' погрешность Hord_Iteraci(a, b, ee, xn, fnx, n, ListBox1) 'процедура метод Хорд vivod(xn, TextBox4) 'Значения корня x vivod(fnx, TextBox5) 'Значение функции при корне f(x) vivodint(n, TextBox6) 'количество итераций End Sub End Class 4.2 Результаты расчёта при точности E = 0.01, E=0.001, E = 0.0001 При погрешности 0,01 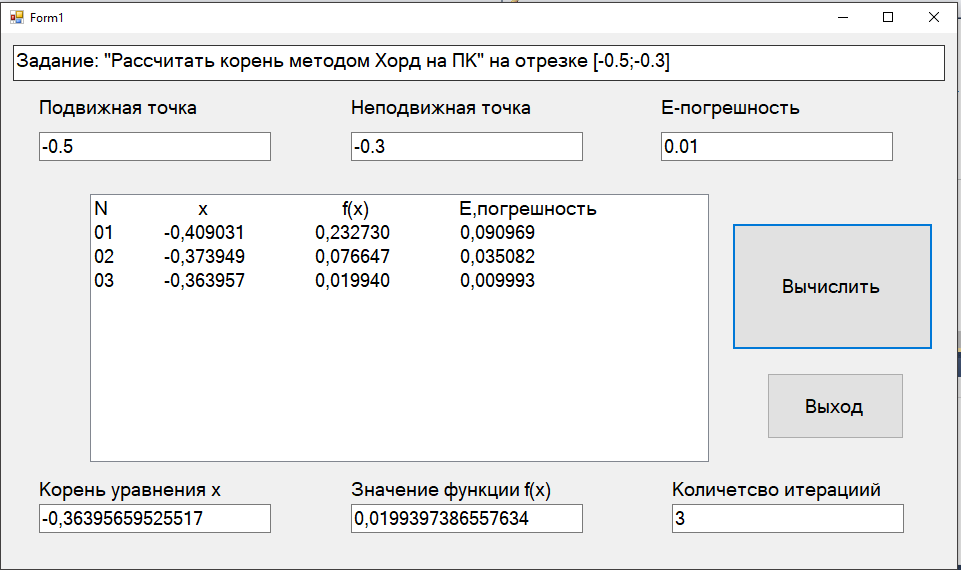 При погрешности 0,001 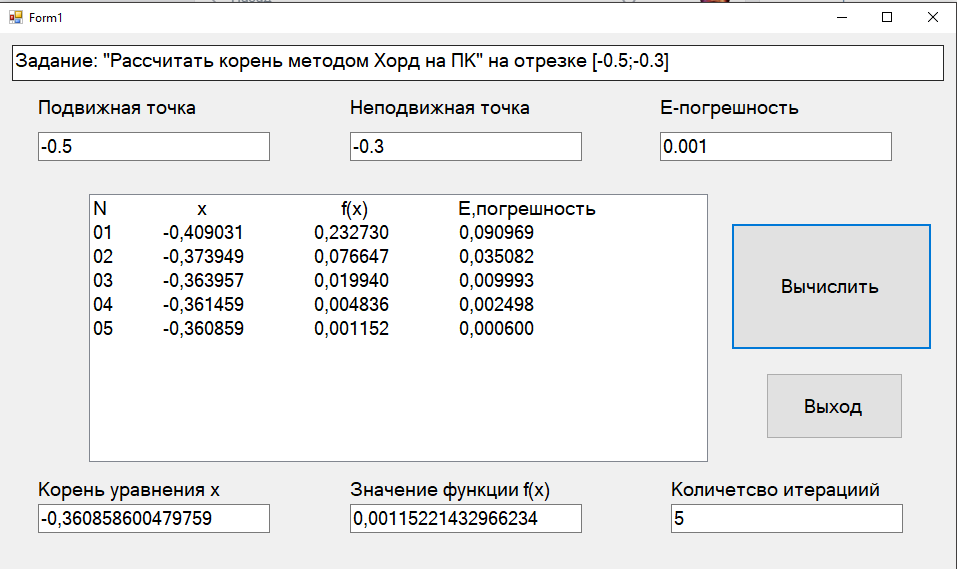 При погрешности 0,0001 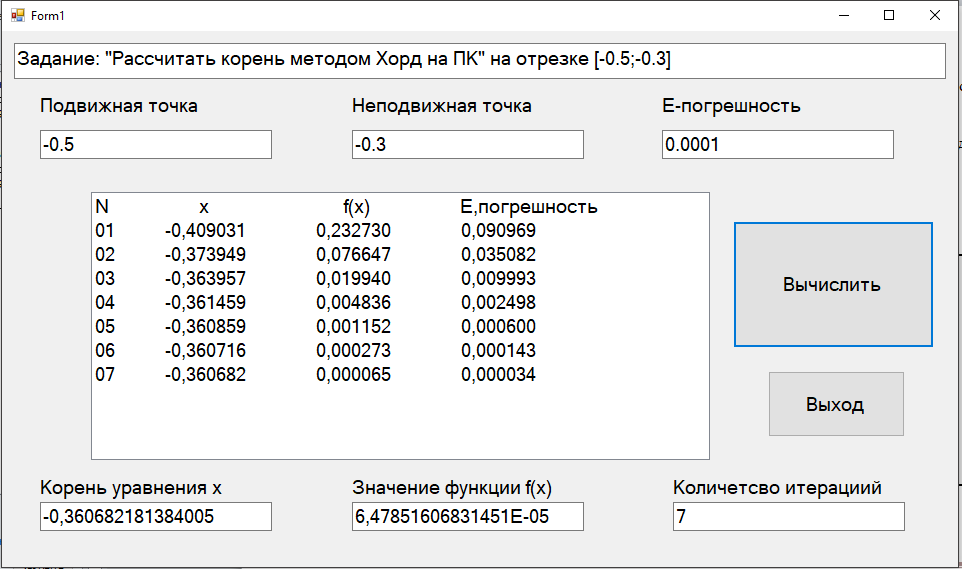 4.3 Схемы алгоритма для процедур программы 1)схема процедуры-подпрограммы Hord_Iteraci (), вычисления корня методом хор 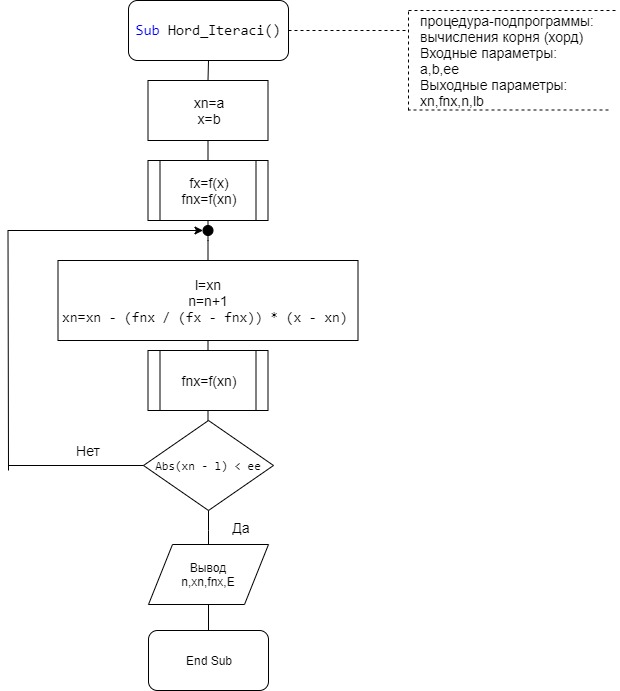 2)схема процедура-функция: для вычисления значений нашей функции «x-sin(1/x)» 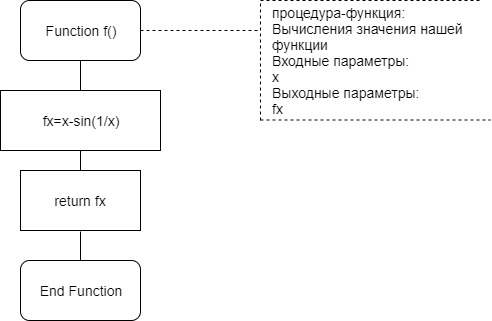 4.4 Результаты расчёта на ПК 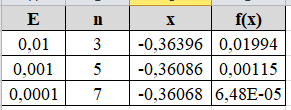 4 5 Зависимость числа итераций от точности в логарифмическом масштабе
 |
