Методическая разработка для сро по теме Математическая статистика
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
1 2 Методическая разработка для СРО по теме: Математическая статистика Для описания и объяснения наблюдаемых процессов и явлений исследуются статистические данные, которые представляют собой количественные характеристики каких либо объектов. Они формируются под действием множества факторов, название из которых доступны внешнему контролю. Рассмотрим совокупность статистических данных, представляющих собой набор наблюдаемых значений одной или нескольких переменных, характеризующих изучаемое явление или объект. Под генеральной совокупностью подразумевается все возможные наблюдения некоторого показателя (признака), все исходы случайного испытания или всю совокупность реализаций случайной величины X(ω). Например, под генеральной совокупностью понимают данные о доходах жителей какой-либо страны, результаты голосования населения по какому-либо вопросу и т. д. Выборочной совокупностью или просто выборкой называется совокупность случайно отобранных объектов, взятых из генеральной совокупности объемом N. Выборка объема n - это результат наблюдения случайной величины в вероятном эксперименте, который повторяется n раз в одних и тех же условиях. Объемом совокупности называется число объектов этой совокупности. Выборку называют репрезентативной (представительной), если она достаточно полно представляет изучаемые признаки и параметры генеральной совокупности. Для того, чтобы выборка была репрезентативной, необходимо обеспечить случайность отбора, с тем чтобы все объекты генеральной совокупности имели равные вероятности попасть в выборку. Варианты и их частоты. Произведем из генеральной совокупности выборку объема n. Наблюдаемые значения случайной величины X: x1, x2,…xk называются вариантами. Вариационным рядом называется последовательность вариант записанных в возрастающем порядке. Разложение статистических данных по не убыванию называется ранжированием статистических данных. Если наблюдаемые значения варианты xi повторяются, то число появлений значений xi называются частотами и обозначаются ni, а их отношения к объему выборки - относительными частотами, т.е. Статистическим распределением случайной величины X называется перечень вариант xi и соответствующих им частот ni или относительных частот wi, при этом Для характеристики вариационного ряда по аналогии с теорией вероятностей строится эмпирическая функция распределения. Эмпирической (статистической) функцией распределения называется функция F*(x),определяющая для каждого значения x относительную частоту события X < x: где nx – число наблюдении, при которых наблюдались значения признака Х, меньших чем х; n - объем выборки. 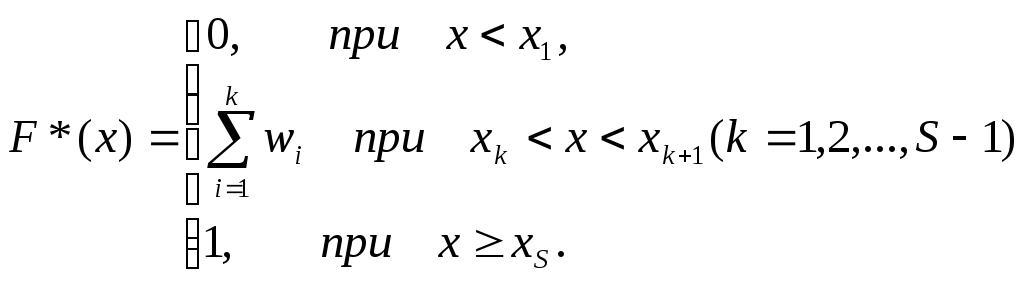 (4) (4)Эмпирическая функция F*(x) обладает всеми свойствами теоретической (интегральной) функции распределения F(x). Из теоремы Бернулли следует, что при увеличении числа n наблюдений относительная частота события X Таким образом, эмпирическая функция распределения F*(x) является оценкой теоретической функции распределения F(x) случайной величины Х. Числовые характеристики статистического распределения. Для характеристики статистического распределения рассмотрим ряд числовых величин, аналогичных ранее данных в теории вероятностей. Выборочным средним или где wi – относительная частота. В случае интервального статистического ряда в качестве xi берут середины его интервалов, а среднее значение отклонений равно нулю: поэтому для характеристики рассеяния наблюдаемых значений Х вокруг среднего значения Выборочной дисперсией Для практических расчетов удобнее использовать формулу: где: Для возврата к единицам измерения изучаемого признака Х возьмем корень квадратный из выборочной дисперсии, который называется выборочным средним квадратичным отклонением: Для практических расчетов используется величины: которая называется исправленной выборочной дисперсией, а величина S - исправленным средним квадратичным отклонением. Начальным эмпирическим моментом порядка k называется среднее арифметическое k - x степеней значений выборки: Центральным эмпирическим моментом порядка k называется среднее арифметическое k - x степеней отклонений значений выборки от выборочной средней В частности, т.е. центральный эмпирический момент второго порядка равен выборочной дисперсии. Коэффициентом вариации вариационного ряда называется процентное отношение среднего квадратичного отклонения к выборочному среднему: Коэффициентом асимметрии эмпирического распределение называется число и эксцессом вариационного ряда называется число: Кроме перечисленных числовых характеристик для вариационного ряда используются мода, методы и размах вариации. Размахом вариации называется число R равное разности между наибольшей и наименьшей вариантами: Модой Мо* вариационного ряда называется варианта, которая имеет наибольшую частоту. Медианой Ме* вариационного ряда называется варианта, которая делит вариационный ряд на две равные части, если n=2k, то Задача. Анализируется выборка из 100 малых предприятий. Цель исследования – найти соотношения заемных и собственных средств (xi) на каждом i-м предприятии. Результаты представлены в таблице 1. Таблица 1. Результаты исследования 185 117 187 132 169 132 142 152 136 145 126 153 159 148 149 145 177 113 162 144 125 153 148 168 152 169 163 155 154 145 138 154 166 113 195 173 142 162 171 163 135 152 159 177 192 152 178 166 155 179 138 139 149 151 165 179 165 169 155 163 102 116 151 143 146 166 143 152 148 155 134 182 131 146 175 148 162 122 159 151 174 136 168 161 174 149 155 157 154 146 153 148 159 157 165 117 128 157 168 149 Требуется: 1) Составить интервальный вариационный ряд; 2) Построить полигон, гистограмму, кумуляту и эмпирическую функцию; 3) Вычислить числовые характеристики интервального ряда. Решение. 1. Построим сгруппированный ряд наблюдений (таблица 2), для этого: а) Определим в выборке б) Разобьем весь диапазон [ отсюда длина интервала равна Таблица 2.
2. Построим полигон частот, соединяя точки ( 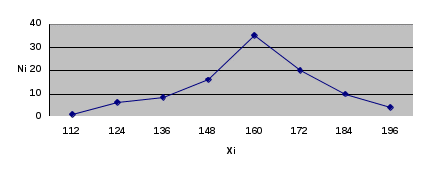 3. Построим гистограмму частот (относительных частот), откладывая по оси абсцисс – xi, а по оси ординат плотность частот – 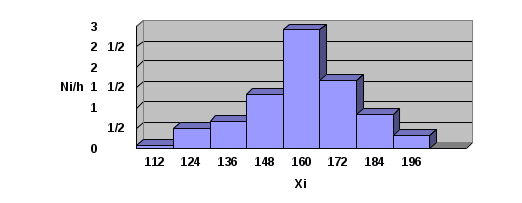 4. Построим кумулятивную кривую (кумуляту) – кривую накопленных частот, при этом соединим точки ( 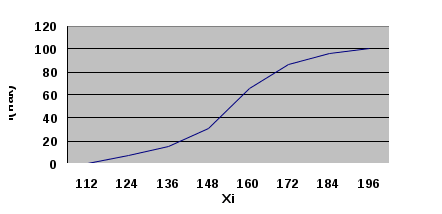 5. Найдем эмпирическую функцию и постоим ее график: 1) x<100, F(x)=0; 2) x<112, F(x)=0,01; 3) x<124, F(x)=0,01+0,06=0,07; 4) x<136, F(x)= 0,07+0,08=0,15; 5) x<148, F(x)= 0,15+0,16=0,31; 6) x<160, F(x)= 0,31+0,35=0,66; 7) x<172, F(x)= 0,66+0,20=0,86; 8) x<184, F(x)= 0,86+0,10=0,96; 9) x<196, F(x)= 0,96+0,04=1. 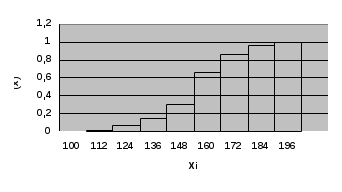 6. Найдем выборочное среднее по выборке: 7. Найдем X2выб: 8. Найдем выборочную дисперсию Dв и исправленную выборочную дисперсию S2: 9. Найдем среднеквадратичное отклонение 10. Найдем размах вариаций: 11. Найдем моду вариационного ряда: 12. Найдем медиану: Задания. Даны наблюденные значения обследуемого количественного признака. Требуется: 1) составить интервальный вариационный ряд; 2)построить полигон, гистограмму, кумуляту и эмпирическую функцию; 3) вычислить числовые характеристики интервального ряда; 4) найти доверительный интервал для математического ожидания а нормального распределения, если доверительная вероятность γ = 0,95. Билет № 1. 169 163 157 154 146 174 161 168 185 154 131 128 152 136 145 169 139 187 158 185 149 155 122 169 151 175 146 132 174 174 198 162 152 155 146 148 151 134 158 154 166 143 169 143 163 165 151 149 102 102 179 165 157 155 168 148 159 158 138 134 149 145 177 113 179 192 113 159 126 138 152 178 166 155 163 195 177 166 125 152 173 142 162 171 145 152 168 148 138 139 117 142 155 168 149 165 157 159 135 125 Билет № 2. 253 228 254 252 241 239 216 231 236 207 225 238 235 226 238 202 234 262 286 258 258 246 266 259 243 249 261 274 268 267 257 268 277 218 259 251 243 246 261 232 265 262 295 292 248 265 253 275 274 269 269 273 252 249 279 262 248 249 232 217 263 242 278 245 265 243 262 255 242 258 255 262 266 277 269 263 257 257 246 245 268 245 268 279 268 243 269 251 254 236 249 271 255 213 255 252 254 258 252 222 Билет № 3 25 53 48 68 52 69 63 55 54 45 38 54 66 13 95 73 42 62 71 63 35 52 59 77 92 52 78 66 55 79 26 41 53 59 48 49 45 77 13 62 38 39 49 51 65 79 65 69 55 63 2 16 51 43 46 66 43 52 48 55 34 82 31 46 75 48 62 22 59 51 74 36 68 61 74 49 55 57 54 46 85 7 87 32 69 32 42 52 36 45 53 48 59 57 65 17 28 57 68 49 Билет № 4 302 338 314 324 342 321 338 309 336 321 336 324 312 320 356 322 302 336 323 334 334 292 362 364 366 362 304 312 310 304 304 298 362 304 328 378 322 322 368 292 292 342 321 340 332 316 296 380 314 324 324 338 352 290 304 298 322 302 298 331 331 331 304 318 282 332 296 312 324 338 324 325 302 332 330 342 324 360 322 334 334 324 332 354 314 316 323 342 360 304 304 314 326 324 304 326 308 334 343 302 Билет № 5 7,8 9,7 12,8 10,6 16,0 13,6 16,9 11,5 10,5 9,7 11,7 12,3 12,3 15,3 9,8 12,4 16,6 9,9 12,9 15,9 9,1 14,8 5,9 9,7 10,8 9,0 15,1 10,7 7,1 11,6 13,7 6,2 6,9 11,0 14,1 16,2 12,9 14,9 16,1 12,5 12,3 12,4 12,9 15,4 12,1 9,3 13,6 15,9 9,4 11,7 6,7 11,5 13,9 9,6 11,3 9,8 9,2 13,4 13,8 12,3 5,6 8,7 9,7 11,9 15,7 10,1 17,6 16,8 8,8 12,1 6,1 11,4 12,0 14,4 14,9 13,6 12,8 6,4 13,0 10,5 12,9 13,7 13,6 10,6 15,9 10,3 17,6 12,1 8,6 12,1 7,4 11,1 6,7 13,0 15,2 13,9 10,8 12,0 11,8 12,3 Билет № 6 759 747 755 747 753 748 760 764 762 754 750 750 751 756 762 730 742 737 740 751 750 750 762 750 751 735 742 743 756 746 756 739 748 733 758 760 758 748 771 751 779 751 750 752 766 738 751 747 752 759 757 746 752 750 757 747 752 754 747 754 767 758 763 763 769 752 762 754 745 749 760 750 739 749 739 747 740 754 745 752 743 758 744 754 746 750 733 750 757 755 745 758 764 745 750 746 756 756 755 765 Билет № 7 336 304 302 338 326 314 320 308 342 304 312 348 336 325 314 308 324 321 322 324 338 323 334 292 312 312 364 356 302 362 381 310 304 298 362 361 304 366 304 298 302 368 292 242 368 290 340 325 304 316 296 314 324 338 324 322 290 331 332 298 360 298 331 331 352 326 318 304 296 332 342 312 324 325 304 316 332 362 322 342 334 322 334 324 302 328 364 330 338 316 322 350 304 314 332 340 324 314 324 326 Билет № 8 101,6 102,3 101,1 98,8 136,7 94,4 91,1 92,3 95,7 83,4 98,0 98,0 97,0 98,0 144,8 96,6 95,7 95,2 94,3 82,9 101,0 91,8 89,1 90,5 142,1 105,0 95,0 105,0 104,0 93,0 104,6 100,6 91,8 92,5 76,3 98,8 96,8 95,5 107,0 85,0 97,2 106,6 95,2 98,5 118,8 97,7 96,1 95,1 96,2 86,2 97,2 106,0 105,9 94,6 114,0 93,4 91,6 89,5 90,2 93,5 103,7 94,8 93,5 104,7 116,0 92,7 89,3 91,0 93,0 129,0 93,9 101,0 92,4 89,9 86,9 108,5 92,5 103,5 105,0 108,0 101,0 81,8 100,0 100,0 86,3 98,0 93,2 95,9 95,8 118,0 97,6 97,9 97,2 98,7 81,4 95,6 104,6 95,6 105,3 92,0 Билет № 9 359 357 365 369 363 355 368 349 325 399 348 368 352 373 342 362 371 345 336 303 366 377 395 352 378 366 355 363 335 320 359 313 392 349 345 377 313 379 336 319 353 359 348 379 365 369 355 368 338 384 349 351 365 366 343 352 343 363 302 327 351 343 346 348 362 357 369 355 334 314 331 346 375 349 356 352 354 361 374 383 368 361 374 332 342 357 336 345 365 396 387 332 369 317 328 305 322 354 346 353 Билет № 10 448 458 454 452 441 439 416 482 436 407 449 445 463 479 468 463 455 451 446 445 468 471 455 413 485 443 469 454 436 454 455 462 466 477 469 452 457 422 457 452 463 478 442 465 443 462 455 442 428 442 469 473 452 449 479 466 448 449 438 417 465 432 495 492 448 485 446 475 474 469 457 468 477 413 459 451 443 446 481 432 459 448 466 459 453 449 451 431 468 487 448 458 454 452 441 139 416 482 436 407 Билет № 11 172 143 163 172 146 153 169 148 138 139 179 165 157 155 168 148 159 158 138 134 168 163 157 154 146 174 161 168 185 154 132 128 152 136 145 169 139 187 158 185 149 155 122 168 151 175 146 132 174 176 198 162 152 155 146 148 151 134 158 154 166 143 169 143 163 165 151 149 102 104 149 145 177 113 179 192 113 159 126 138 152 178 166 155 163 195 177 166 125 156 118 142 155 168 149 165 157 159 135 165 Билет № 12 261 243 279 245 265 243 262 255 242 258 257 268 277 218 259 251 243 246 261 232 258 246 266 259 243 249 261 274 268 267 253 228 254 255 249 239 216 231 236 207 225 238 235 226 238 212 234 262 286 258 258 246 266 259 243 249 261 274 268 267 265 262 295 292 248 265 253 276 274 269 269 273 252 249 279 262 248 249 232 217 255 262 266 277 269 263 257 276 246 245 268 245 268 279 268 243 269 251 254 236 249 271 255 213 255 254 254 258 262 222 Билет № 13 185 117 187 132 169 132 142 152 136 145 126 153 159 148 149 145 177 113 162 144 125 153 148 168 152 169 163 155 154 145 138 154 166 113 195 173 142 162 1 71 163 135 152 159 177 192 152 178 166 155 179 138 139 149 151 165 179 165 169 155 163 102 116 151 143 146 166 143 152 148 155 134 182 131 146 175 148 162 122 159 151 174 136 168 161 174 149 155 157 154 146 153 148 159 157 165 117 1 28 157 168 149 Билет № 14 376 337 368 361 374 349 355 357 354 346 338 339 359 356 365 379 3 65 369 355 363 353 348 359 367 365 317 338 359 358 349 325 353 348 368 352 369 363 355 354 345 338 354 366 313 395 373 342 362 371 363 335 3 52 359 377 3 92 352 378 366 355 379 326 341 353 359 348 349 345 377 313 362 302 316 351 343 346 366 343 352 348 355 334 382 331 346 375 348 362 322 359 351 375 307 387 332 369 332 342 352 336 345 Билет № 15 56 77 91 98 102 66 87 81 111 130 93 83 95 72 95 84 102 112 55 113 84 101 103 96 101 75 97 114 79 98 107 119 116 106 115 105 113 121 104 125 108 102 62 85 109 89 117 69 71 99 112 117 118 88 117 93 123 91 89 105 95 103 94 93 104 94 105 124 107 127 96 118 76 102 128 81 116 76 87 139 102 107 117 103 125 116 126 108 114 148 97 119 104 115 138 92 129 107 117 109 Билет № 16 43 72 75 61 81 85 57 75 51 59 62 101 73 55 74 82 54 75 63 43 82 79 64 101 64 86 62 82 109 38 58 73 77 76 79 39 76 64 56 91 44 61 66 69 84 57 65 83 22 97 78 79 72 68 78 87 71 65 115 99 88 71 67 72 85 45 68 89 95 46 89 86 83 79 87 82 74 65 59 35 74 84 62 73 88 31 69 67 94 51 92 71 98 104 109 94 81 112 44 92 Билет № 17 112 66 72 74 89 52 101 92 98 53 73 33 62 83 74 43 75 64 42 81 54 84 78 94 63 93 73 57 82 93 79 97 95 75 71 82 72 65 73 112 55 87 49 85 32 86 66 83 87 74 75 97 76 105 77 97 78 67 65 66 44 104 56 74 64 81 65 58 68 99 72 62 63 79 122 72 68 82 71 102 51 119 57 73 61 74 69 95 75 103 89 78 59 76 81 69 106 59 72 67 Билет № 18 96 86 72 112 142 106 96 73 114 92 115 94 105 87 95 85 86 104 94 85 65 97 77 87 96 114 73 116 127 103 98 86 137 146 84 97 117 92 95 129 87 96 104 92 154 84 124 93 104 93 124 88 95 83 109 117 132 98 126 66 96 103 96 107 72 98 118 108 92 89 114 102 97 83 109 99 133 81 91 85 123 93 118 71 94 82 95 107 78 105 82 115 75 111 106 79 71 64 106 127 Билет № 19 76 89 127 102 88 95 117 107 167 108 108 95 78 105 89 101 126 106 135 119 81 86 93 154 122 114 72 88 103 107 103 94 116 104 93 128 107 94 112 127 119 84 123 105 83 129 102 132 103 99 123 106 135 93 74 136 116 134 115 163 113 95 124 104 95 101 86 152 104 92 118 108 117 102 87 91 127 141 105 114 106 103 133 98 115 105 119 147 114 85 94 89 125 107 115 92 127 94 143 138 Билет № 20 95 88 98 157 129 109 72 76 115 97 119 84 123 105 83 129 102 132 103 99 128 105 146 99 76 134 116 134 115 166 104 85 124 104 95 101 86 152 104 92 115 104 108 115 87 91 125 146 95 118 109 103 133 98 115 105 114 147 114 85 118 97 137 107 86 101 126 106 136 113 94 89 125 107 115 91 127 94 143 134 108 86 124 109 88 95 117 107 125 105 101 94 116 104 93 128 107 91 112 125 Билет № 21 114 93 106 168 148 133 132 152 133 143 121 114 142 134 123 112 137 121 138 122 126 108 135 129 128 103 102 117 121 118 136 82 127 139 144 148 132 128 135 105 93 141 106 131 123 147 134 116 134 99 131 143 132 127 145 133 117 127 135 85 112 148 144 154 156 163 174 157 162 158 152 153 135 124 144 134 146 118 107 146 125 124 136 119 143 107 136 112 147 124 139 125 137 118 149 138 148 144 145 137 Билет № 22 139 125 137 118 149 138 148 144 145 137 131 143 132 127 145 133 117 127 135 85 152 153 135 124 144 134 146 118 107 146 117 83 109 178 158 143 132 152 133 143 121 114 142 134 123 112 137 121 138 122 121 108 135 129 128 103 102 117 127 118 139 82 127 139 144 148 132 128 135 105 93 141 106 136 123 147 134 116 134 99 115 148 144 154 156 163 174 157 162 158 127 124 136 119 143 107 136 119 157 124 Билет № 23 453 448 459 457 465 412 428 457 468 494 434 482 431 446 475 448 462 422 459 451 485 417 487 432 469 432 442 452 436 445 427 453 451 445 444 445 477 413 462 444 425 453 448 468 452 465 463 455 454 445 436 454 466 413 495 473 442 462 471 463 433 452 459 477 492 452 478 466 455 479 431 439 449 451 465 479 465 469 455 463 402 416 451 443 446 446 443 452 448 445 474 436 468 461 474 449 455 457 454 446 Билет № 24 9,6 11,1 6,7 13,2 15,2 13,9 10,8 12,0 11,8 12,3 14,9 13,7 13,6 10,6 15,9 10,3 17,6 12,1 8,6 12,1 15,3 12,4 12,9 15,4 12,1 8,3 14,9 15,9 9,4 11,7 8,7 11,5 13,9 9,6 11,3 9,8 9,2 13,4 13,8 12,3 7,8 9,7 12,8 10,6 16,0 13,6 16,9 11,5 10,5 9,7 17,7 12,3 12,3 15,3 9,8 12,4 16,6 9,9 12,9 15,9 9,5 14,8 5,9 9,7 10,8 9,0 15,1 10,7 7,1 11,6 12,7 6,2 6,9 11,0 16,5 16,2 12,9 14,9 16,1 12,5 12,9 12,4 12,9 15,4 12,4 9,3 13,6 15,9 9,4 11,7 4,8 8,7 9,7 11,9 15,7 10,1 17,6 16,8 8,8 12,1 6,1 11,4 12,0 14,4 14,9 13,6 12,8 6,4 13,0 10,5 14,9 13,7 13,6 10,6 15,9 11,3 17,6 12,1 8,6 12,1 Материалы для самостоятельной работы обучающегося (СРО): Тема 1. Линейная алгебра. 1.Вычислить алгебраическое дополнение 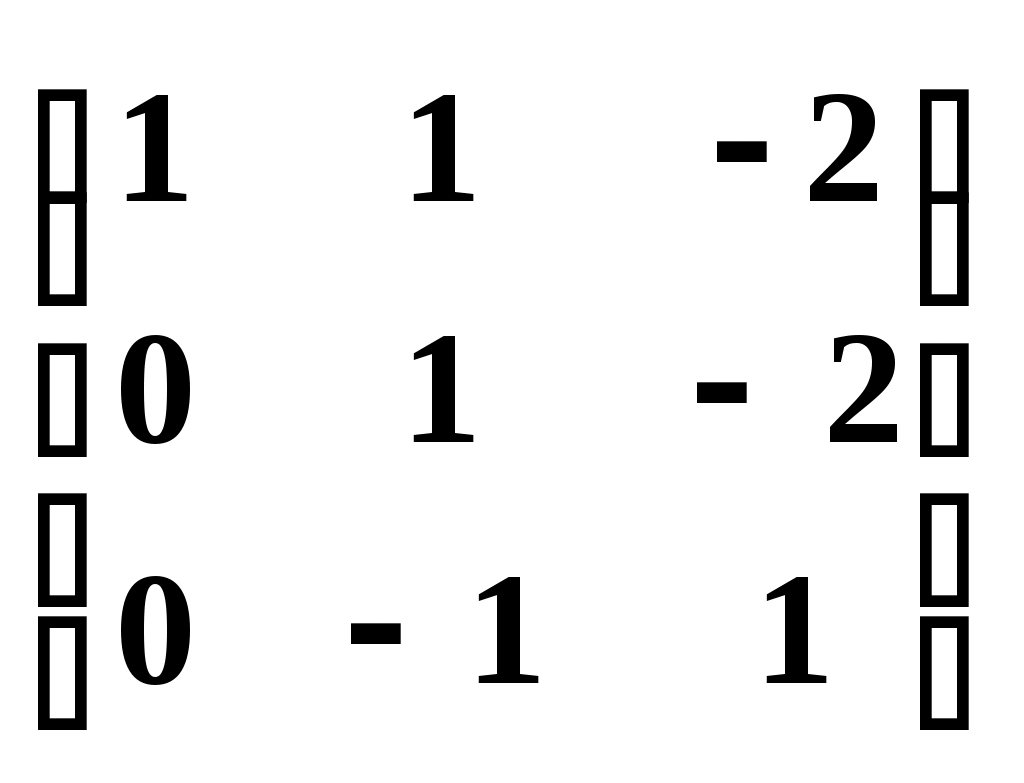 . .2.Найдите линейную комбинацию матриц: 3.Определите размерность произведения матриц 4.Вычислите произведение матриц: 5.Приведите матрицу к ступенчатому виду 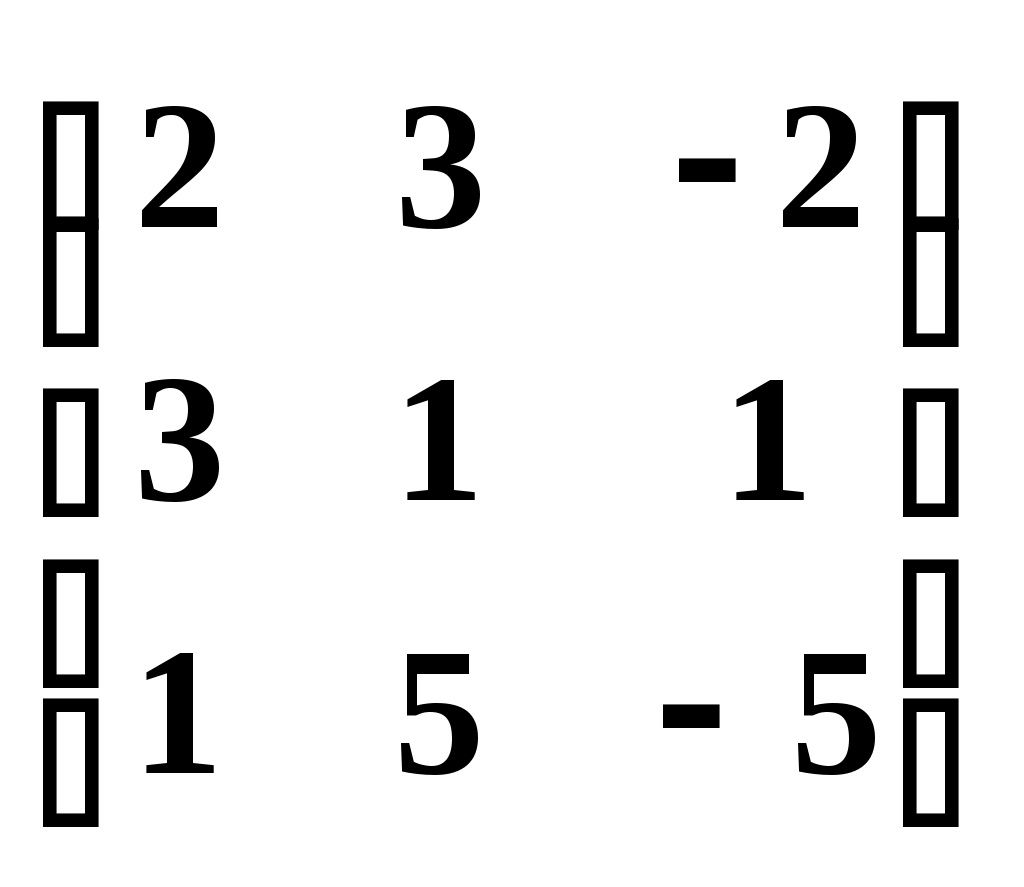 6.Определите ранг матрицы 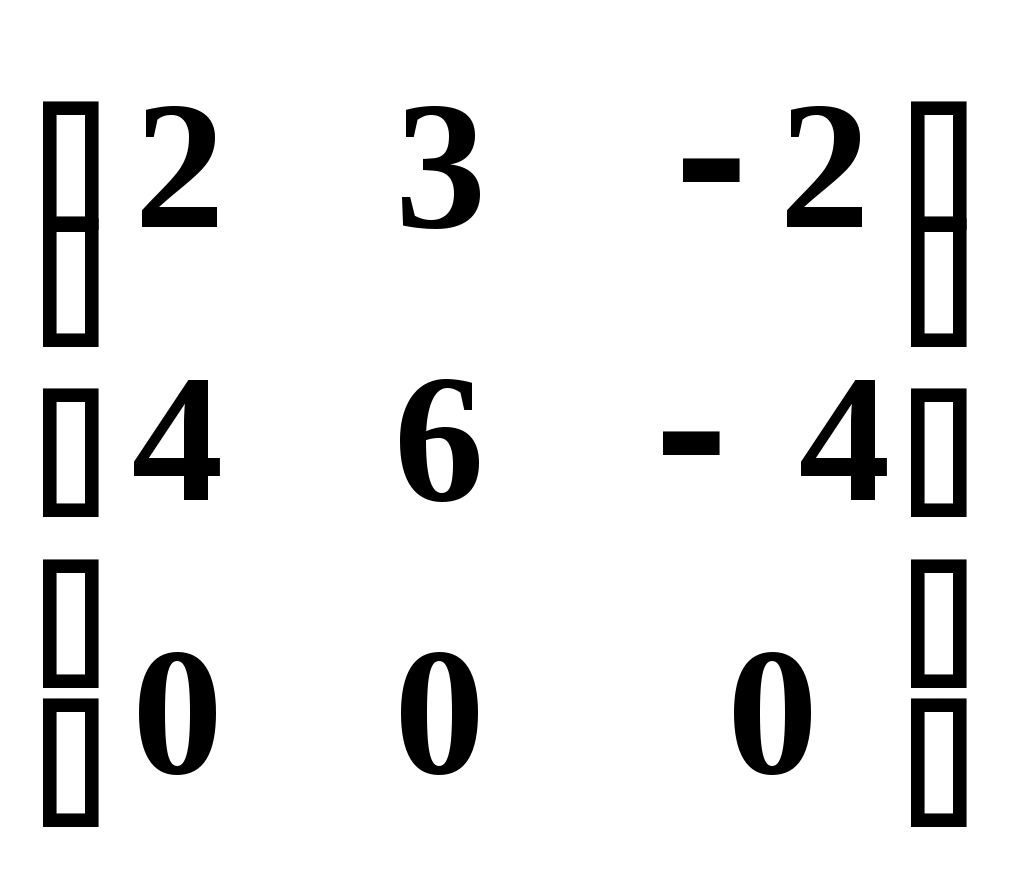 7.Пусть в матрице А порядка n точно n элементов равны 1, а остальные нули. Чему может быть равен определитель матрицы? 8.Вычислить определитель: 9.Решите систему уравнений а)методом Крамера, в) при помощи элементарных преобразований, с) с помощью обратной матрицы. a) 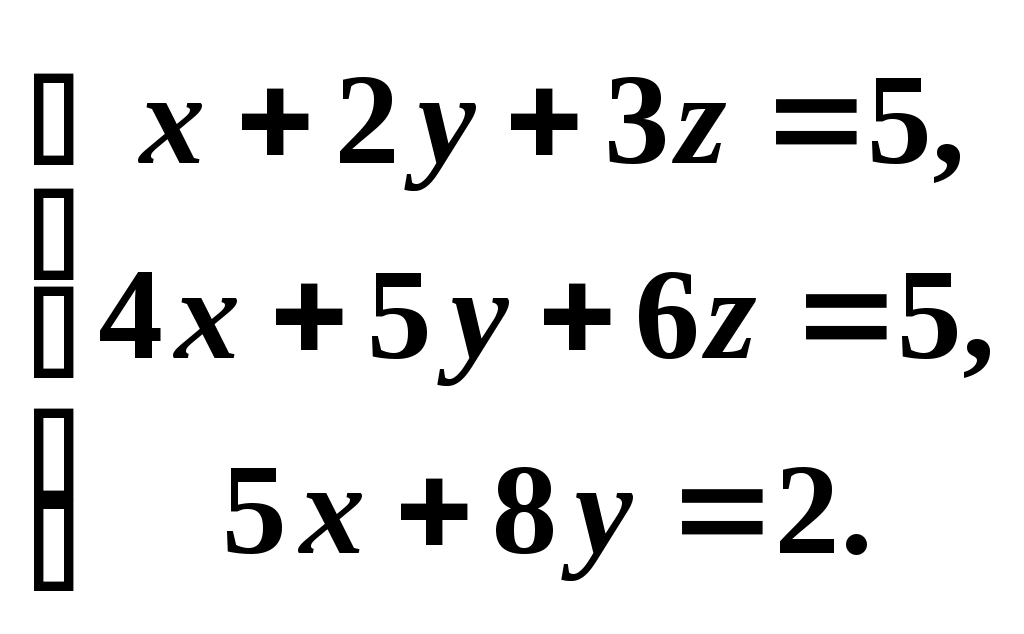 b) b)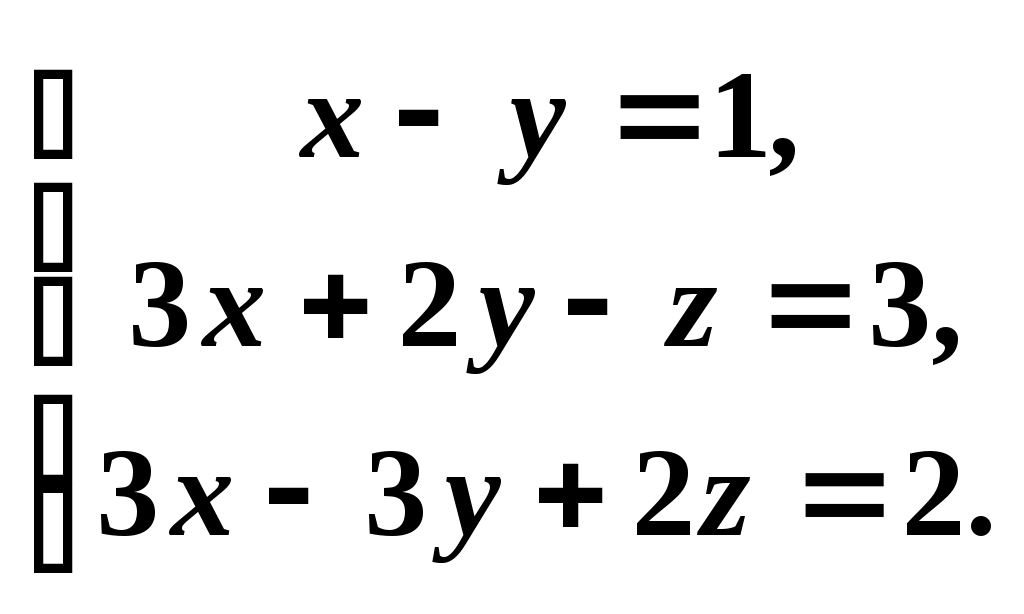 c) c)10.При каких условиях система уравнений, содержащая m уравнений с n неизвестными и рангом r основной матрицы имеет единственное решение? Тема 2. Векторная алгебра. 1.Найти длину вектора 2.Известно, что Вычислить скалярное произведение векторов Найти векторное произведение векторов 2х-у+2z-9=0. 6.Найти длину вектора 7.Известно, что 8.Вычислить скалярное произведение векторов 9.Найти векторное произведение векторов 10.Найти длину вектора 11.Известно, что 12.Вычислить скалярное произведение векторов 13.Найти векторное произведение векторов Тема 3. Аналитическая геометрия. 1.Даны вершины треугольника А(1;-1;1), В(2;3;4) и С(4;3;2). Вычислить длину его высоты, опущенной из вершины А на сторону ВС. 2.Дано уравнение плоскости 2x-y-3z-12=0. Написать для нее уравнение “в отрезках”. 3.Написать уравнение плоскости, проходящей через три точки: А(0;-2;5), В(6;6;0) и С(3;-3;6). 4.Вычислить расстояние от точки Q(3;4;-7) до плоскости 2х + 3у + z -6 = 0. 5.Даны вершины треугольника А(1;-1;1), В(2;1;-1) и С(-1; -1;-2). Вычислить длину его высоты, опущенной из вершины А на сторону ВС. 6.Дано уравнение плоскости 2x-3y+6z+12=0. Написать для нее уравнение “в отрезках”. 7.Написать уравнение плоскости, проходящей через три точки: А(2;-1;-2), В(1;2;1) и С(5;0; -6). 8.Вычислить расстояние от точки Q(3;4;-7) до плоскости 5х-2у+3z-10=0. 9.Даны вершины треугольника А(2;3;-6), В(6;4;4) и С(3;7;4). Вычислить длину его высоты, опущенной из вершины В на сторону АС. 10.Дано уравнение плоскости x+5y+2z-10=0. Написать для нее уравнение “в отрезках”. 11.Написать уравнение плоскости, проходящей через три точки: А(1;-1;2), В(2;1;2) и С(1;1;4). 12.Вычислить расстояние от точки Q(5;1;-1) до плоскости х-2у-2z+4=0. Тема 4. Введние в анализ.
Тема 5. Производная функции. ТАБЛИЦА ПРОИЗВОДНЫХ
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Тема 6. Функция многих переменных. 1.Найти частные производные функции: 1) z =x4 +4 xy2 + 3x + 4, 2) z =x3 + 5x2y2 - 7x, 3) z =x4 + 5xy2 + 5x, 4) z =3x3 +у3- xy2 + 6x, 5) z =x3 +6у2- 3xy2 + 5x + 3у, 6) z =5x3 +у3+ 6x2y2 + 6x + 3у, 7) z =3x4 +4у4- 3xy2 + 5x + 3у, 8) z =2x3 +у3 +5xy2 + 5x + 6у + 7, 9) z =5x3 +4у3- 3x2y2 + 7xу + 3у, 10) z =3x3 +2у3+ 6xy2 -3x +4у. Тема 7. Неопределенный интеграл. 1 2 |
