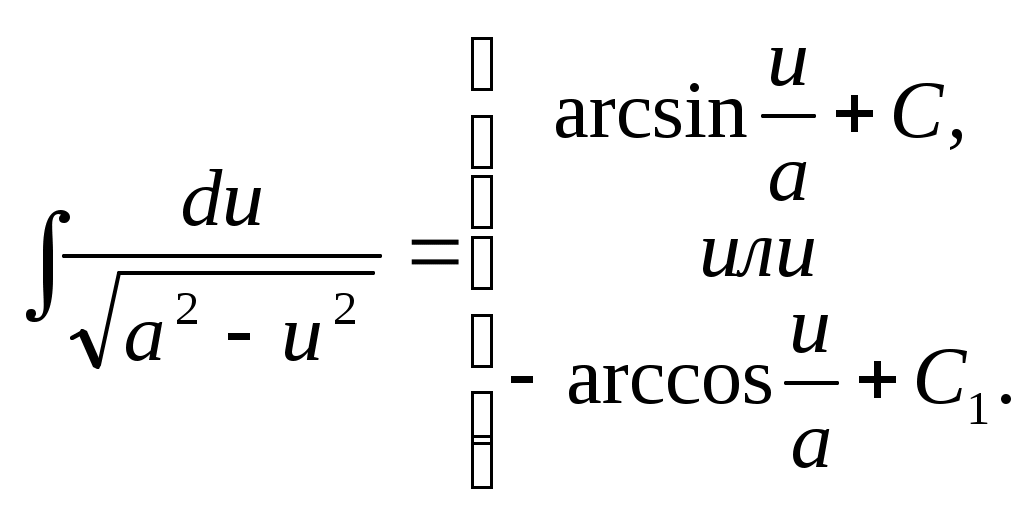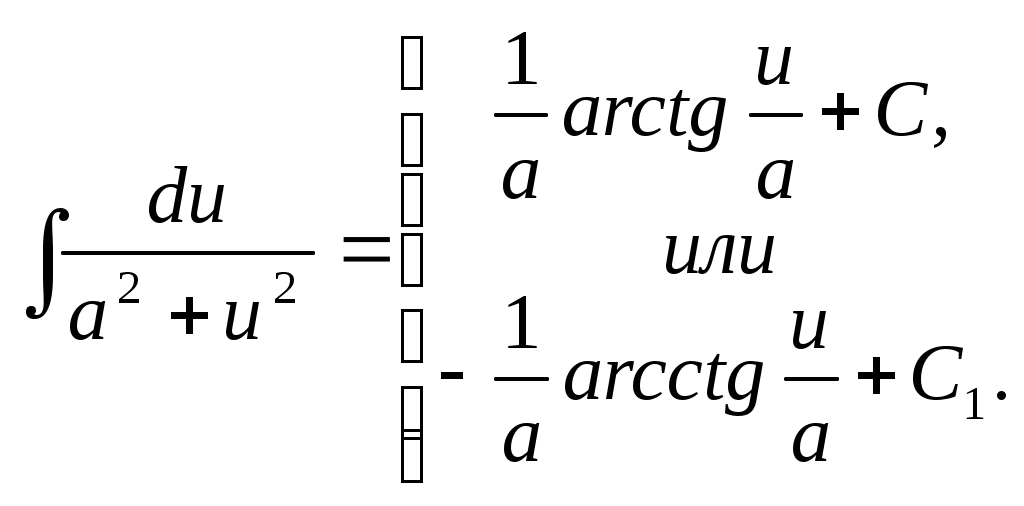Методическая разработка для сро по теме Математическая статистика

• Название: Методическая разработка для сро по теме Математическая статистика
• Дата: 11.01.2023
• Размер: 0.58 Mb.
• Имя файла: metod.ukazaniya po sro (1).doc
• Тип: Методическая разработка; #880986
• страница: 2 из 2

ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ

1. .	12.
2.	13.
3.	14.
4.	15.
5.	16.
6.	17.
7.	18.
8.	19.
9.	20.
10.	21.
11.	22.

Тема 8. Определенный интеграл.

Вычислить площадь фигуры, ограниченной данными линиями. Сделать чертеж.

1.	xy = 4, y = x, x = 4.	6.	(x2+y2)2 = 9(x2-y2), x2+y2=4, (x2+y2³4).
2.	y = x2, 4y = x2, y = 4.	7.	(x2+y2)2 = 16(x2-y2), x2+y2=9, (x2+y2³9).
3.	y2 = 4+x, x + 3y = 0.	8.	(x2+y2)2 = 9(x2-y2), x2+y2=1, (x2+y2³1).
4.	(x2+y2)2=4(x2-y2), x2+y2=1, (x2+y2³1).	9.	(x2+y2)2 = 25(x2-y2), x2+y2=9, (x2+y2³9).
5.	(x2+y2)2 = 2(x2-y2), x2+y2=1/2, (x2+y2³1/2).	10.	y2 –6y + x2 =0, y2 –8y + x2 =0, y = x, x = 0.

Тема 9. Теория вероятностей.

Билет № 1.

1. Какова вероятность извлечь и колоды в 52 карты:

а) карту пиковой масти;

в)фигуру любой масти или карту масти пик?

2. В тире имеется 5 ружей, вероятность попадания из которых соответственно равны 0,5; 0,6; 0,7;0,8;0,9. Определить вероятность попадания, если ружье выбирается наудачу.

3. Что вероятнее выиграть у равносильного противника: 3 партии из 5, или 5 из 8?

4. Какова вероятность того, что в столбике из 100 наугад отобранных монет, число монет, расположенных гербом вверх будет от 45 до 55?

Билет № 2.

1. Из колоды в 52 карты наудачу вынимают 3 карты. Найти вероятность того, что среди них хотя бы один туз.

2. Со склада поступило 9 деталей, из них 2 прошли ОТК. Вероятность того, что изделие, прошедшее ОТК, имеет первый сорт – 0,8, а для не прошедшего ОТК эта вероятность 0,1. Взятая наудачу деталь оказалась первого сорта. Какова вероятность того, что она прошла ОТК.

3. Для прядения смешаны поровну белый и окрашенный хлопок. Какова вероятность среди 7 случайно выбранных волокон смеси обнаружить 2 окрашенных?

4. Вероятность попадания в цель равна 0,4. Произведено 1600 выстрелов. Какое отклонение относительной частоты от вероятности по модулю ожидать вероятность большей чем 0,9?

4. Вероятность неточной сборки прибора равна 0,2. Найти вероятность того, что среди 500 приборов окажется от 410 до 430 точных.

Билет № 3

1. Вероятность выигрыша на один билет 0,15. Какова вероятность хотя бы одного выигрыша для владельца 7 билетов.

2. Вероятность появления события А равно 0,4. Какова вероятность того, что при 5 испытаниях событие А появится более 3 раз?

3. Имеются две урны: в первой – 6 белых шара и 4 черных; во второй 5 белых и 3 черных. Из первой урны во вторую перекладывают, не глядя, два шара. После этого из второй урны берут один шар. Найти вероятность, что этот шар не будет черным.

4. В ящике 5 белых, 4 черных и 7 синих шаров. Вынули один шар. Вычислить вероятность того, что вынутый шар: 1) белый или черный; 2) белый или синий.

Билет № 4.

1.Бросают игральную кость. Какова вероятность выпадения номера 4 на верхней грани упавшей на стол кости. Какова вероятность выпадения номера больше 4.

2. Прибор может работать в двух режимах: 1) нормальном и 2) ненормальном. Нормальный режим наблюдается в 80% всех случаях работы прибора; ненормальный – 20%. Вероятность выхода прибора из строя за время Т в нормальном режиме равна 0,1; в ненормальном - 0,7. Найти полную вероятность выхода прибора из стоя за время Т.

3. Предполагается, что 10% новых открывающихся предприятий прекращают свою деятельность в течении года. Какова вероятность того, что из шести малых предприятий не двух в течении года прекратят свою деятельность.

4. Производство дает 0,01% брака. Какова вероятность того, что из взятых на исследований 1000 изделий выбраковано будет не больше 2.

Билет № 5

1. 
   Вероятность попадания в цель первым стрелком равна 0,75, а вторым стрелком - 0,7. Стрелки выстрелили одновременно. Какова вероятность того, что один попадет в цель, а другой не попадет.
   
2. 
   Имеется три одинаковых по виду ящика. В первом ящике 15 белых шаров и 5 черных, во втором 10 белых и 8 черных шаров. В третьем – 5 белых и 15 черных шара. Из выбранного наугад ящика вынули белый шар. Вычислить вероятность того, что шар вынут из первого ящика.
   
3. 
   Монету подбрасывают 7 раз. Какова вероятность того, что она упадет гербом вверх не более трех раз.
   
4. 
   В течении часа коммутатор получает с среднем 60 вызовов. Какова вероятность того, что за время 1 мин., в течении которого телефонистка отлучилась, будет не более двух вызовов.
   

Билет № 6.

1. 
   Вероятность выигрыша на один билет 0,18. Какова вероятность хотя бы одного выигрыша для владельца шести билетов.
   
2. 
   На фабрике изготовляющей болты, первая машина производит 35%, вторая – 25%, третья – 40% всех изделий. В их продукции брак составляет соответственно 6, 4, и 3 %. Какова вероятность того, что случайно выбранный болт дефектный.
   
3. 
   Предполагается ,что 15% открывающихся новых малых предприятий прекращают свою деятельность в течении года. Каков вероятность того, что из пяти малых предприятий не более двух в течении года прекратят свою деятельность.
   
4. 
   В магазин поступило 4000 набора канцелярских принадлежностей. Вероятность того, что набор содержит недостаточно или избыточное количество канцелярских товаров, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено два ошибочно укомплектованных набора.
   

Билет № 7.

1. 
   В первом ящике находятся шары с номерами от 1до 5, а во втором – с номерами 6 до 10. Из каждого ящика вынули по одному шару. Какова вероятность того, что сумма номеров вынутых шаров: 1) не меньше 8; 2) равна 11.
   
2. 
   В классе 12 мальчиков и 8 девочек . Нужно выбрать делегацию из трех человек. Какова вероятность того, что выбраны два мальчика и одна девочка.
   
3. 
   Для контроля продукции, состоящей из четырех партий, наудачу взято одно изделие. Как велика вероятность обнаружить брак, если в партиях 0.4; 0,2; 0,3; 0,2 соответственно деталей бракованные.
   
4. 
   В среднем по 25% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из восьми договоров с наступлением страхового случая будет связано с выплатой три договора.
   

Билет № 8

1.Сборщик получил 3 ящика деталей: в первом – 25, из них – 10 окрашенных, во втором -25 , из них 8 – окрашенных , в третьем – 12, из них – 8- окрашенных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика окажется окрашенной.

2. Какова вероятность того, что из 3 наудачу взятых карт две карты вальты, если в коде 36 карт.

3. Имеются два одинаковых ящика с шарами. В первом ящике 5 белых и 3 черный шар, во втором – 6 белых и 7 черных шара. Наудачу выбирают один ящик и вынимают из него шар. Какова вероятность того, что вынутый шар окажется черным?

4. Всхожесть семян данного сорта растений оценивается с вероятностью равной 0,7. Какова вероятность того, что из 6 посеянных семян взойдут не менее 4?

Билет № 20.

1. Среди 40 деталей 8 нестандартные. Взяты наудачу 4 детали. Найти вероятность того, что они нестандартные.

2. Достаточным условием сдачи коллоквиума является ответ на один из двух заданных преподавателем вопросов. Какова вероятность того, что студент сдаст коллоквиум, если он не выучил 10 из 30 вопросов.

3. Для контроля продукции, состоящей из 4 партий, наудачу взято одно изделие. Как велика вероятность, обнаружить брак, если в одной из партий 1/3 изделий бракованные, а в остальных четырех все годные?

4. Среднее число вызовов, поступающих на АТС в минуту, равно 120. Найти вероятность того, что за 3 секунды на АТС не поступит ни одного вызова.

Билет № 22.

Какова вероятность извлечь из колоды в 52 карты:

а) карту червовой масти;

б) фигуру любой масти.

2. В ящике 15 деталей, среди которых 5 нестандартных. Найти вероятность того, что в наудачу отобранных деталях окажется не более одной нестандартной детали.

3. Имеются две урны: в первой -9 белых шара и 5черных; во второй 7белых и 6 черных. Из первой урны во вторую перекладывают, не глядя, два шара. После этого из второй урны берут один шар. Найти вероятность, что этот шар не будет черным.

4. Вероятность попадания в цель при каждом выстреле равна 0,002. Найти вероятность попадания в цель двух и более пуль, если число выстрелов равно 3000.

Билет № 23.

1. Среди 12 деталей 5 нестандартных. Взяты наудачу 3 детали. Найти вероятность того, что среди них хотя бы одна стандартная.

2. Рабочий обслуживает 3 станка. Вероятность выхода из строя за смену для них соответственно равна 0,7; 0,8; 0,9. Найти вероятность того, что за смену выйдут из строя точно два станка.

3. Вероятность попадания при каждом выстреле для 3 станков равны соответственно 4/5, ¾ , 2/3. При одновременном выстреле всех трех стрелков имелось два попадания. Определить вероятность того, что промахнулся третий.

4. Всхожесть семян растения составляет 70%. Какова вероятность того, что из 10 посеянных семян взойдут хотя бы девять.

Билет № 25.

1.В магазин поступила партия из 36 изделий, в которой 8 изделий имеют повреждения. Какова вероятность того, что из взятых наугад 4 изделий хотя бы одно изделие является поврежденным.

2. На предприятии работают две бригады рабочих: первая производит в среднем 0,3 продукции с процентом брака 5 %, вторая - 0,7 продукции с процентом брака 4 % . Найти вероятность того, что взятое наугад изделие окажется бракованным.

3. Какова вероятность того, что из шести посеянных семян взойдут не менее четырех , если всхожесть семян арбузов равна 0,8

4. На станциях отправления поездов находятся 2000 автоматов для продажи билетов. Какова вероятность того, что в течении часа из строя выйдут три автомата, если вероятность выхода из строя одного автомата равна 0,002.

Литература: 1, 2, 3, 4, 5, 9, 10, 11, 12, 14, 15, 16.

Темы докладов и рефератов.

Метод наименьших квадратов.

Поверхности второго порядка.

Приложение производной в экономике.

Эластичность функции.

Метод Симпсона, трапеций и прямоугольников.

Приложение определенного интеграла в экономике.

Задачи по экономике, приводящие к дифференциальным уравнениям.

Приложение линейной алгебры в экономике.

Приближенное решение дифференциальных уравнений.

Преобразование декартовой системы координат: параллельный перенос и поворот осей координат.

Кривые в полярной системе координат.

Приложение аналитической геометрии в экономике.

Модель Леонтьева.

Числовые характеристики случайных величин.

Числовые характеристики статистических величин.