основные понятия тригонометрии. Основные понятия тригонометрии. Методическая разработка основные понятия тригонометрии Подготовила учитель математики Смирнова Галина Васильевна
 Скачать 0.7 Mb.
|
|
Задания для самостоятельного решения Определить знак числа  Расположить в порядке возрастанияSin 140o, Sin 190o, Sin 280o. Определить знак числа  Расположить в порядке возрастания  Определить знак числа  Расположить в порядке возрастания  Определить знак числа  Определить знак числа  Определить знак числа  Определить знак числа  Расположить в порядке возрастания  Определить знак числа  Расположить в порядке возрастания  Определить знак числа  Расположить в порядке возрастания  Определить знак числа  Расположить в порядке возрастания  Определить знак числа  Расположить в порядке возрастания  Определить знак числа  Определить знак числа Определить знак числа Определите знак числа  Определите знак числа  Определите знак числа  Найти значение выражения  Найти значение выражения 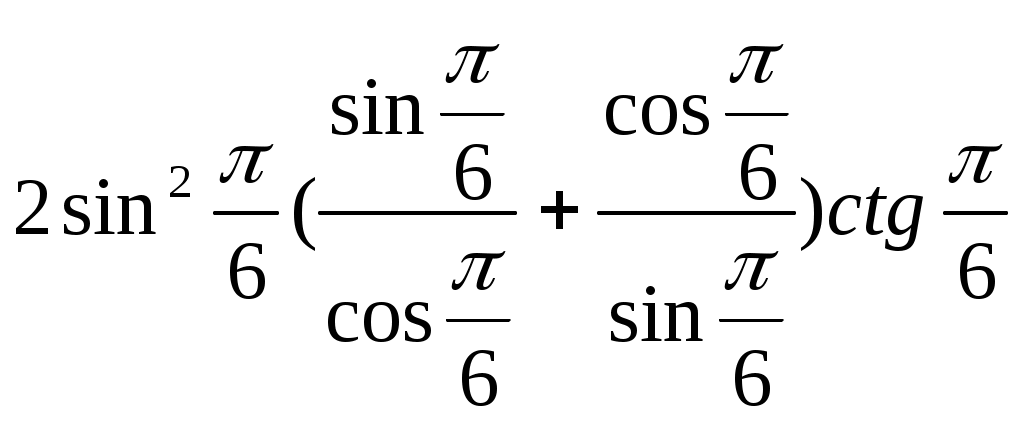 Найти значение выражения  Найти значение выражения при   Найти значение выражения при   Найти значение выражения при  и   Найти значение выражения при и  Алгебраические соотношения между тригонометрическими функциями одного и того же аргумента sin 2x + cos 2x = 1   1 + tg 2 x =  1 + ctg 2 x =  tgx ctg x = 1 С помощью данной группы формул и знания знака тригонометрических функций можно находить значения всех тригонометрических функций угла по значению одной из них. Задания с решением. 1.Найти значения синуса, тангенса и котангенса угла  , если  и  < < Решение Рассмотрим основное тригонометрическое тождество для угла sin 2 + cos 2 = 1 и подставим в него вместо  его значение  .Получим sin 2 +  = 1 Тогда sin 2 = 1- ; sin 2 = 1  ; sin 2 =  Будем извлекать квадратный корень с учетом того, что < < ( то есть угол лежит в 1У четверти), а синус в этой четверти отрицателен. Получаем sin =  = Найдем теперь тангенс угла 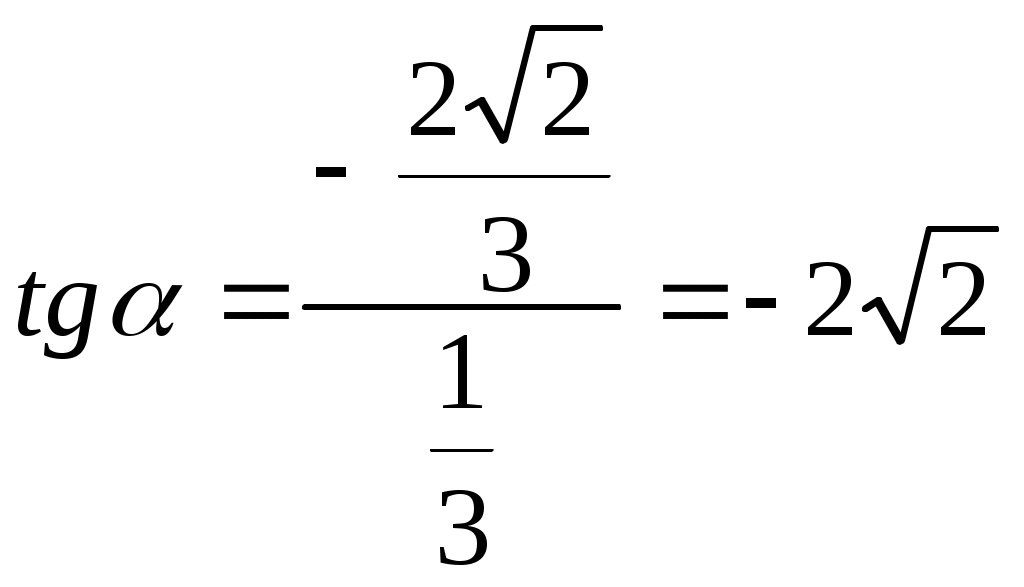.Имеем  , то есть  .Так как tg ctg = 1, то  Ответ sin = ; ; 2. Найти значения синуса, косинуса и котангенса угла , если  и < < Решение Так как tg ctg = 1, то  Рассмотрим тригонометрическое тождество для угла 1 + tg 2 =  и подставим в него вместо  его значение  .Получим  Тогда ;  ;  .Будем извлекать квадратный корень с учетом того, что < < ( то есть угол лежит в 1У четверти), а косинус в этой четверти положителен. Получаем  Для того, чтобы найти синус угла рассмотрим основное тригонометрическое тождество для угла sin 2 + cos 2 = 1 и подставим в него вместо его значение  .Получим sin 2 +  = 1 Тогда sin 2 = 1- ; sin 2 =  ; sin 2 =  Будем извлекать квадратный корень с учетом того, что < < ( то есть угол лежит в 1У четверти), а синус в этой четверти отрицателен. Получаем sin =  = Ответ ; ;  Формулы сложения аргументов sin ( х + у ) = sin х cos у + cos х sin у sin ( х у ) = sin х cos у cos х sin у cos ( х у ) = cos х cos у + sin х sin у cos ( х + у ) = cos х cos у sin х sin у   Задания с решением. 1.Найти  Решение  Ответ  2.Вычислить  Решение  Ответ  3. Найти  Решение 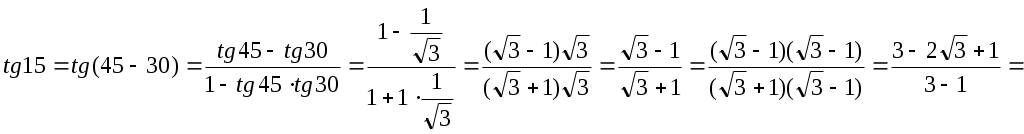  Ответ  Формулы двойного аргумента cos 2х = cos 2х sin 2х sin 2х = 2 sin х cos х tg 2x =  Следствие из формул двойного аргумента 1 + cos 2х = 2 cos 2х 1 cos 2х = 2 sin 2х Задания с решением. 1.Вычислить  Ответ 8 2. Вычислить  Ответ 48 |