основные понятия тригонометрии. Основные понятия тригонометрии. Методическая разработка основные понятия тригонометрии Подготовила учитель математики Смирнова Галина Васильевна
 Скачать 0.7 Mb.
|
|
Государственное бюджетное общеобразовательное учреждение Средняя общеобразовательная школа №531 Красногвардейского района Санкт-Петербурга МЕТОДИЧЕСКАЯ РАЗРАБОТКА Основные понятия тригонометрии Подготовила учитель математики Смирнова Галина Васильевна г. Санкт-Петербург 2015 Основные понятия тригонометрии Расширение понятия угла В тригонометрии мы рассматриваем угол как фигуру, полученную поворотом луча вокруг его начальной точки Луч может вращаться против часовой стрелки – тогда получаем положительные углы. Если луч вращается по часовой стрелке, то угол считается отрицательным. Таким образом мы можем получить углы любой величины. При этом разные по величине углы могут иметь одинаковые начальные и конечные стороны. Радианная и градусная мера угла Углы измеряются в градусах и радианах. Один градус ( обозначение 1° ) – это поворот луча на 1 / 360 часть одного полного оборота. Таким образом, полный оборот луча равен 360°. Один градус состоит из 60 минут ( их обозначение 1‘ ); одна минута – соответственно из 60 секунд ( обозначаются 1“ ). Угол в 1 радиан, это центральный угол, который опирается на дугу окружности, длина которой равна длине радиуса. 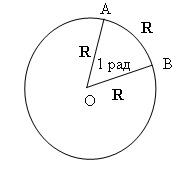 Чтобы найти радианную меру угла надо найти отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги. Справедливы формулы зависимости между радианной и градусной мерой. Таблица значений наиболее часто встречающихся углов в градусах и радианах:
Тригонометрический круг. Поворот точки вокруг начала координат Для понимания тригонометрии необходимо освоить понятия, связанные с, так называемым, тригонометрическим кругом. Тригонометрический круг — построенная на плоскости с прямоугольными декартовыми координатами окружность, имеющая центр в точке начала координат и радиус, равный 1. 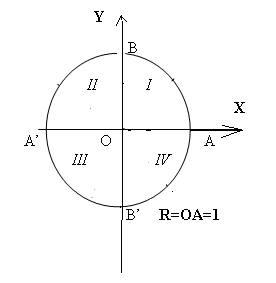 В этой окружности рассматривают два диаметра: горизонтальный AA’ и вертикальный BB’. Они делят плоскость на четыре координатные четверти. У всех рассматриваемых углов начальная сторона будет совпадать с лучом ОА. Если конечная сторона угла лежит в какой-то четверти, то говорим, что это угол лежит в этой четверти. Каждому углу 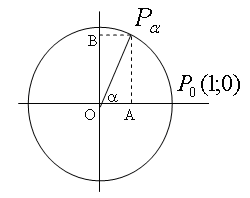 на единичной окружности соответствует единственная точка , полученная поворотом точки  на угол . Если углы равны, то точки совпадают, но если точки совпали, то углы отличаются на  , где k- некоторое целое число.Каждому числу tна числовой прямой мы можем сопоставить точку  на единичной окружности. Для этого необходимо повернуть точку на угол t радиан.Синус, косинус, тангенс и котангенс Рассмотрим на координатной плоскости окружность единичного радиуса с центром O в начале координат. Повернем точку  (1;0) на угол . Получим точку .Косинусом угла α называется абсцисса x точки 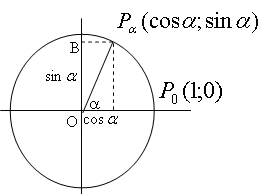.Синусом угла α называется ордината y точки .При этом тангенсом угла α называется отношение синуса этого угла к косинусу, а котангенсом угла α называется отношение косинуса этого угла к его синусу.   Вычисление значений тригонометрических функций. Используя определения тригонометрических функций можно найти значения тригонометрических функций часто используемых в тригонометрии углов.
Знаки синуса, косинуса и тангенса. Из определения тригонометрических функций следует, что синус положителен там, где положительна ордината, то есть в 1 и11 четверти. Косинус положителен в 111 и 1У четвертях, а тангенс в 1 и 111. 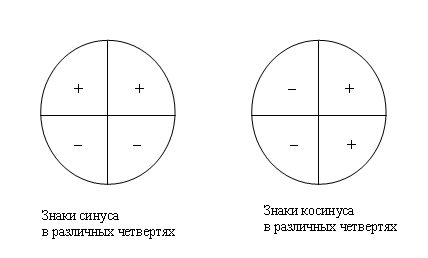 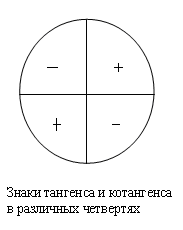 Синус, косинус и тангенс углов a и - a. Из определения тригонометрических функций следует, что косинус -функция четная, а синус, тангенс и котангенс – нечетные, то есть 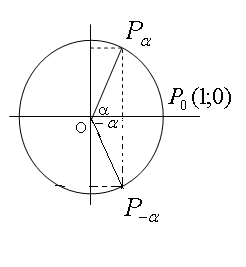     Задания с решением. 1. Найти значение выражения  Решение. Находим в таблице значения тригонометрических функций нужных нам углов и подставляем их в данное выражение  Ответ5,5 2. Определить знак числа  Решение Найдем все углы на окружности 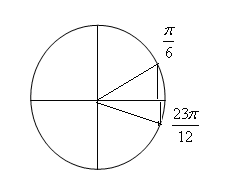 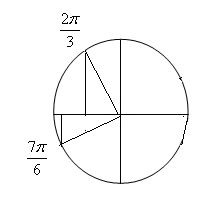- это угол в 1У четверти это угол в 1 четверти  отрицательное число отрицательное число, значит  отрицательное число. это угол 111четверти  это угол второй четверти  отрицательное число отрицательное число, значит  отрицательное число.Произведение двух отрицательных чисел положительно, значит число положительноеОтвет-число положительное 3. Расположить в порядке возрастания  Решение Найдем все углы на окружности 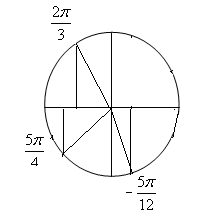это угол второй четверти это угол третьей четверти это угол четвертой четверти Ясно, что  число положительное, а  и  отрицательны.По рисунку видно, что больше чем Ответ , , 4. Вычислить  Решение По свойству четности для косинуса и свойству нечетности для синуса получаем   Тогда  Ответ -12 5.Расположить в порядке возрастания  Решение Найдем все углы на окружности Вспомним, что 1 радиан  Тогда2 радиана – это примерно 114º -это угол второй четверти 4 радиана –это примерно 228º -это угол третьей четверти 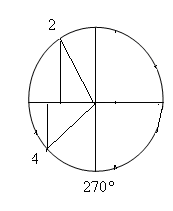  По рисунку видно, что  <  <  Ответ , , |
