основные понятия тригонометрии. Основные понятия тригонометрии. Методическая разработка основные понятия тригонометрии Подготовила учитель математики Смирнова Галина Васильевна
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
ФОРМУЛЫ ПРИВЕДЕНИЯ Вы наверно замечали, что во всех справочных таблицах по тригонометрии указаны значения тригонометрических функций для углов от 0 до 90 градусов. Почему? Потому что значения всех других углов могут быть приведены к значениям функций от углов от 0 до 90 градусов. Помогают в этом так называемые формулы приведения и периодичность тригонометрических функций. Действительно, благодаря периодичности значение тригонометрических функций от любого угла равно значению той же функции от угла в пределах от 0 до С помощью формул сложения можно вывести 32 формулы, которые и называются формулами приведения. В таблице даны формулы приведения для тригонометрических функций.
Подметим закономерности в этих формулах : всегда получается либо та же самая функция, либо кофункция от угла В правой части формулы стоит либо знак « + » либо знак «» Для того, чтобы не запоминать 32 формулы ,запомним правило 1.ПРАВИЛО ВЫБОРА НАЗВАНИЯ ФУНКЦИИ( правило лошади) Если в формуле содержатся углы вида 2. ПРАВИЛО ВЫБОРА ЗНАКА Для того чтобы определить знак в правой части формулы достаточно определить знак левой части формулы, считая угол Задания с решением. 1. Упростить выражение 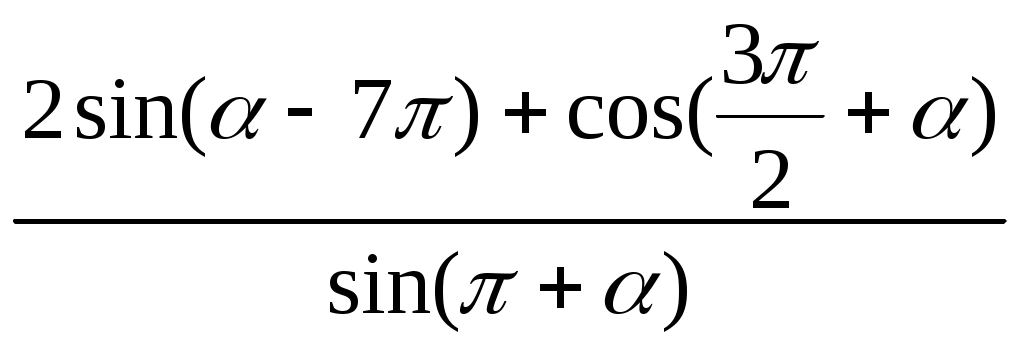 Решение Воспользуемся нечетностью синуса и его периодичностью6 Подставим все в исходное выражение 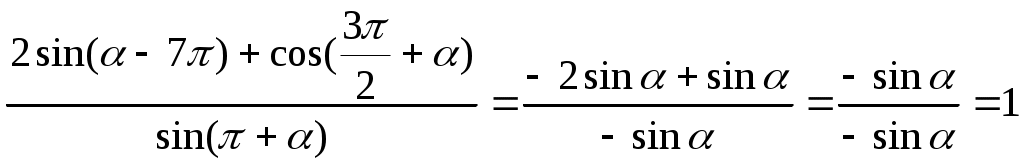 Ответ 1 2.Упростить выражение Решение Ответ -4 Задания для самостоятельного решения Найти значение выражения Найти значение выражения Вычислить Вычислить Вычислить Вычислить Вычислить Вычислить Вычислить Вычислить Вычислить Вычислить Вычислить Вычислить Вычислить Вычислить Вычислить Найдите , если Найдите , если Найдите Найдите Найдите Вычислить , если Вычислить , если Вычислить , если Упростить Упростить Упростить Упростить Упростить Упростить Вычислить Упростить Вычислить Найти значение выражения Найти значение выражения при Найти значение выражения Найти значение выражения .Найти значение выражения Найти значение выражения Найти значение выражения Найти значение выражения Вычислить Вычислить: Найти значение выражения , если Найти значение выражения Найти значение выражения Найдите Найти Найдите Найдите Найдите Найдите Найдите Найдите Найдите , если Найдите , если 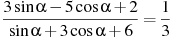 . . Найдите Найдите Найдите |
