Методическая разработка по теме «Построение сечений многогранников». Методическая разработка по теме «Построение сечений многогранник. Методическая разработка по теме Построение сечений многогранников

• Название: Методическая разработка по теме Построение сечений многогранников
• Анкор: Методическая разработка по теме «Построение сечений многогранников
• Дата: 05.04.2022
• Размер: 2.53 Mb.
• Имя файла: Методическая разработка по теме «Построение сечений многогранник.doc
• Тип: Методическая разработка; #445085

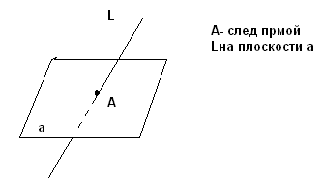
Методическая разработка

по теме

«Построение сечений многогранников»

2022

Пояснительная записка
Данная разработка предполагает ознакомление с основными методами решения задач на построение сечений многогранников с использованием ИКТ, применение которых способствует осознанию понятия движения и тем самым дает возможность визуализировать обучения учащихся поэтапному построению на проекционном чертеже.

Основные цели:

• 
  формирование основ научного мировоззрения, базирующегося на инвариантных и фундаментальных знаниях стереометрии;
  
• 
  формирование основ грамотного построения моделей многогранников;
  
• 
  развитие пространственных представлений и воображения учащихся при помощи специального компьютерного программного обеспечения;
  
• 
  выявление и развитие математических способностей учащихся.
  

Задачи:

• 
  ознакомление учащихся с методами построения сечений многогранников и формирование у них устойчивого интереса к математике, посредством решения задач с использованием ИКТ;
  
• 
  политехническая направленность обучения учащихся путём решения задач прикладного характера;
  
• 
  подготовка к обучению в вузе.
  

Данная разработка может быть предназначена для учащихся X—XI классов различных типов общеобразовательных учреждений и при подготовке к ЕГЭ.
Данная разработка рассчитана на 10 часов.

Содержание разработки:

1. 
   Теоретические основы темы
   
2. 
   Пропедевтика.
   
3. 
   Построение сечений тетраэдра.
   
4. 
   Построение сечений параллелепипеда
   
5. 
   Пересечение двух плоскостей
   
6. 
   Призма
   
7. 
   Задания для контроля
   
8. 
   Литература
   

Теоретические основы темы.
1. Построение точек пересечения прямой и плоскости

Следом прямой L на плоскости α называют точку пересечения прямой L c плоскостью α.
Следом плоскости α на плоскость β называют прямую, по которой плоскость α пересекает плоскость β.

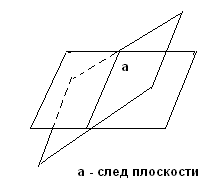
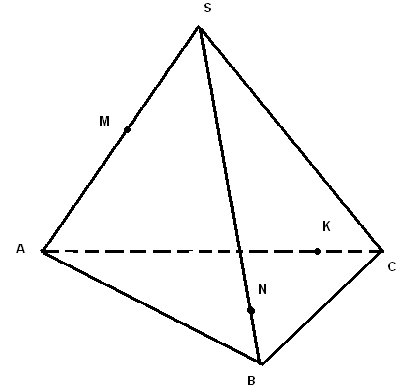
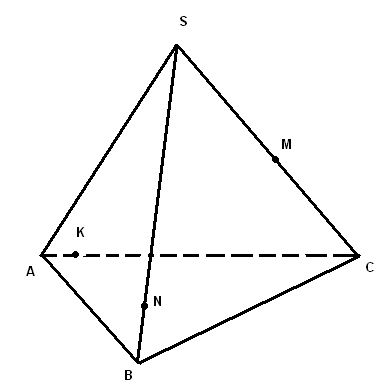
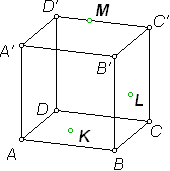
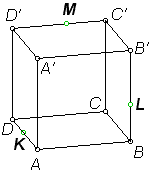
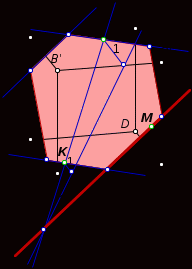
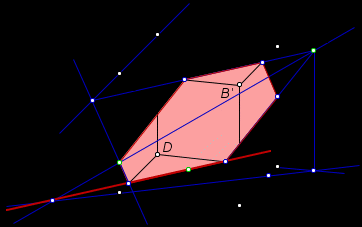
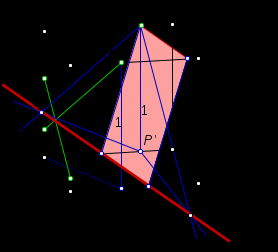
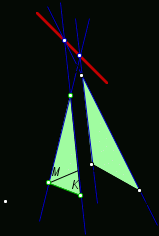
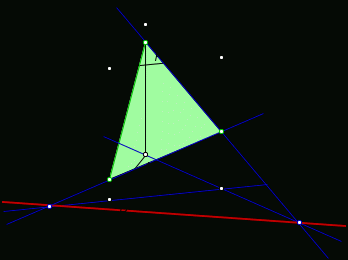
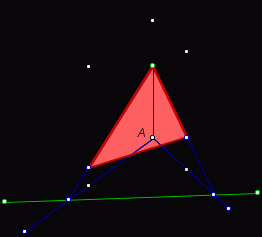
2. Построение плоских сечений многогранников.

Итальянский ученый Леонид Батист Альберти (1404-1472) подчеркивал значение геометрии в живописи и утверждал, что своими художественными представлениями человек обязан именно геометрии. Геометрия была и остается законодательницей моды в вопросах гармонии и красоты.

При решении задач по стереометрии часто необходимо умение строить на рисунке сечения многогранников (например, пирамиды, параллелепипеда, куба и т.д.) некоторой плоскостью. Поясним, что понимается под сечением.

Сечение многогранника плоскостью - многоугольник, представляющий собой множество всех точек пространства, принадлежащих одновременно данному многограннику и плоскости. Данную плоскость называют секущей.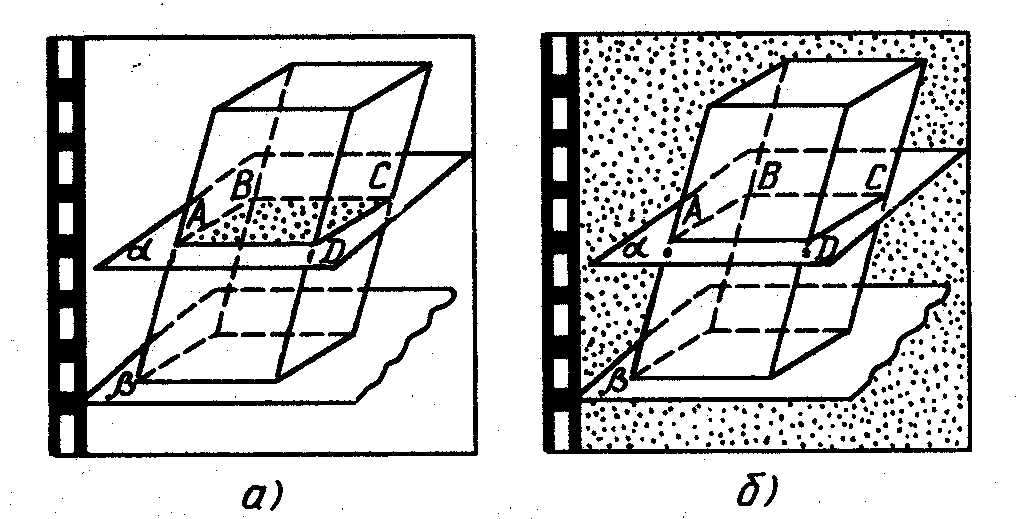



Например, на рисунке изображен параллелепипед и секущая плоскость α, пересекающая параллелепипед по четырехугольнику АВСD. Плоскость β, в которой лежит одна из граней параллелепипеда, секущей плоскостью для него не является.

Для построения сечения многогранника, а точнее его изображения, можно построить точки пересечения секущей плоскости с ребрами многогранника и соединить каждые две из них, лежащие в одной грани.

Последовательность вершин и сторон сечения не существенна, но выполнять построения необходимо с учетом аксиом и теорем стереометрии, а также правил изображения фигур.

А) Для построения прямой, по которой пересекаются некоторые две плоскости и β, нужно построить две их общие точки, тогда прямая, проходящая через эти точки, есть линия пересечения плоскостей и β;

В) Для построения точки пересечения прямой и плоскости нужно построить точку пересечения прямой и прямой m, по которой пересекаются плоскость и любая плоскость, содержащая прямую .

3. Метод внутреннего проектирования

Сущность этого способа заключается в следующем. Имея три точки, определяющие плоскость сечения, находят их проекции на основную плоскость, а также проекцию еще не построенной точки. По трем данным точкам и четырем проекциям отыскивают четвертую точку, принадлежащую плоскости сечения. Таким же образом, получают пятую, шестую и т.д. точки, принадлежащие поверхности геометрического тела и плоскости сечения, т.е. сечению.
Способы задания секущей плоскости:

• 
  тремя точками, которые не лежат на одной прямой;
  
• 
  прямой и точкой, не лежащей на ней;
  
• 
  двумя пересекающимися прямыми и т.д.
  

Методы построения сечений

• 
  метод следов;
  
• 
  метод внутреннего проектирования;
  
• 
  метод переноса секущей плоскости.
  

Тема «Построение сечений тетраэдра».

Цель – помочь изучить раздел геометрии «Построение сечений в стереометрии». Помочь учащимся в развитии пространственного представления, умения мысленно моделировать геометрические тела и строить их графические изображения. Постигая теорию построения учащиеся знакомятся с новыми геометрическими закономерностями, многие из которых на продолжении столетий применяются в производственной практик, используются в архитектуре и живописи.

Рассмотрим метод следов.

Построить сечение многогранника плоскостью - это значит построить прямые, являющиеся следами пересечения граней многогранника данной плоскостью.

Следом прямой L на плоскости α называют точку пересечения прямой L c плоскостью α.
Следом плоскости α на плоскость β называют прямую, по которой плоскость α пересекает плоскость β.

Практический материал. Предложенные задания взяты из “Живой геометрии”, которую можно использовать при наличии интерактивной доски или проектора с функцией интерактивной доски.

	мультипликация
Постройте сечение тетраэдра SABC плоскостью MNK.	Постройте сечение тетраэдра SABC плоскостью MNK.
В тетраэдре SABC точка К лежит в плоскости ABC. Постройте сечение тетраэдра плоскостью MNK.	В тетраэдре SABC точка М лежит в плоскости ASВ. Постройте сечение тетраэдра плоскостью MNK.
В тетраэдре SABC точка О лежит в плоскости ABC, а точка К – на отрезке SO. Постройте сечение тетраэдра плоскостью ACK.	В тетраэдре SABC точка О лежит в плоскости ABC, а точка M – на отрезке SO. Постройте сечение тетраэдра плоскостью BMC.

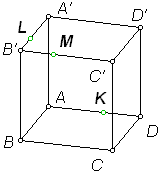
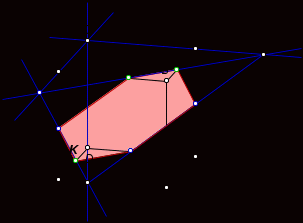
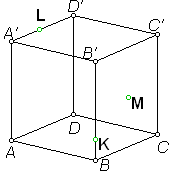
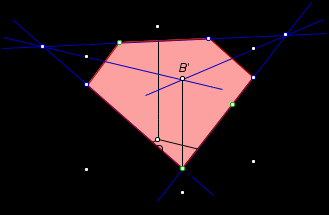
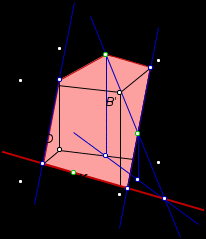
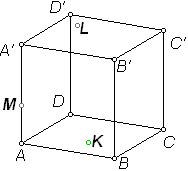
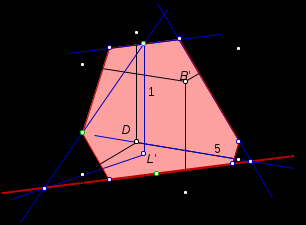
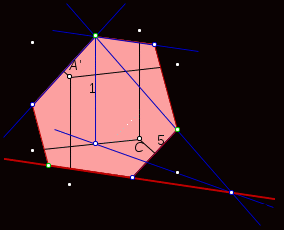
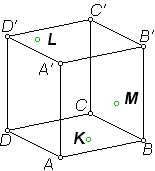
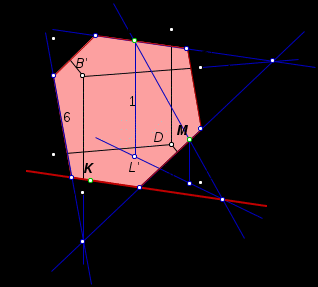
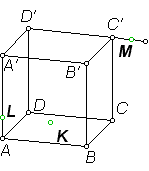
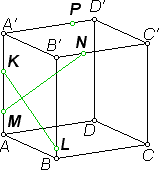
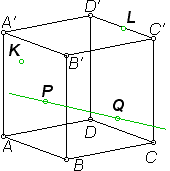
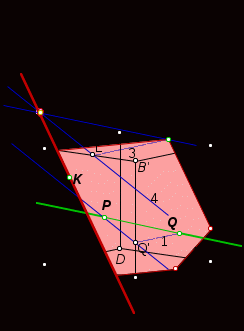
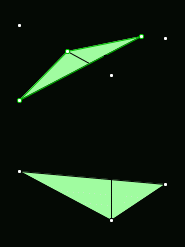
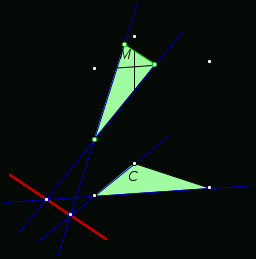
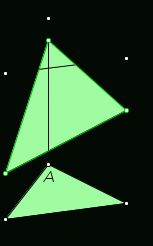
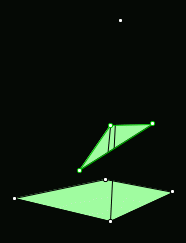
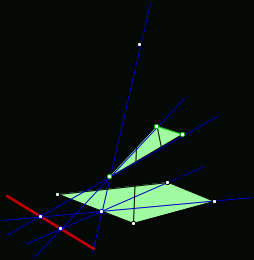
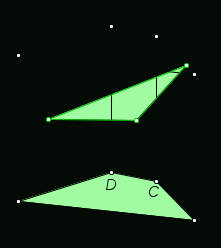
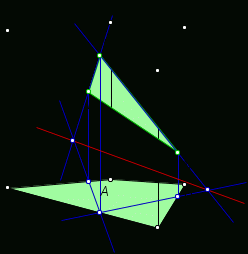
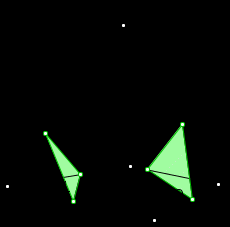
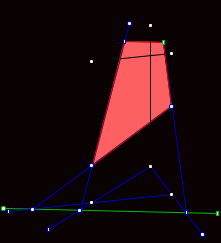
Тема « Построение сечений параллелепипеда».

Цель урока: показать два способа построения сечений параллелепипеда

• 
  способ следов,
  
• 
  способ внутреннего проектирования.
  

 Для освоения начертательной геометрии, машиностроительного, архитектурно-строительного черчения необходимо овладеть некоторыми приемами решения стереометрических задач.

Теоретический материал.

Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырехугольники. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.

Особенность для построения сечения параллелепипеда.

Если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны (свойство 1°, п. 11).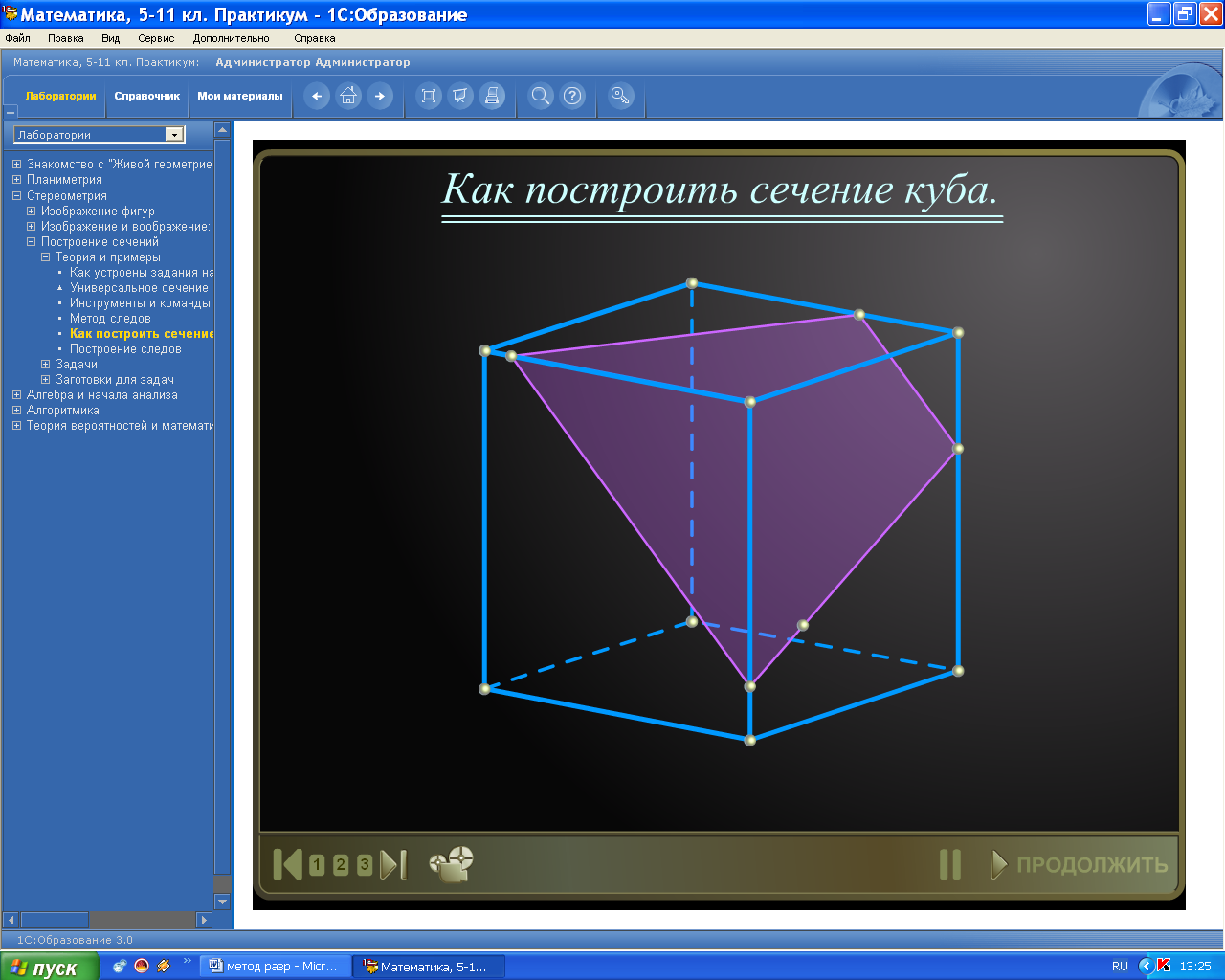

Задача 1. Построить сечение параллелепипеда плоскостью заданной тремя точками P, K и M на ее боковых ребрах.

План построения иллюстрируется мультипликацией.

• 
  Проведем через точки Т и Р прямую а
  
• 
  Проведем прямую b через точки А и В
  
• 
  Обозначим точку их пересечения R
  

• 
  Проведем прямую d через точки T и M
  
• 
  Проведем прямую с через точки В и С
  
• 
  Обозначим точку пересечения R ₁
  
• 
  Соединим прямой х точки R и R₁
  

Точки пересечения прямой x с ребрами AD и DC обозначим X и Y

Многоугольник XPTMY –искомое сечение.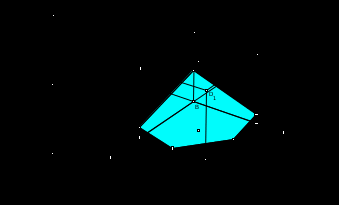

 

Примером построения сечения этим же способом могут сечения этим же способом мо служить следующие иллюстрации:

Задача 2. Дан куб АВСDА₁В₁С₁D₁. Точки О, Е и Т принадлежат ребрам АВ, АD и СС соответственно. Постройте сечение куба плоскостью, проходящей через точки О, Е и Т.

Решение (см. рис.)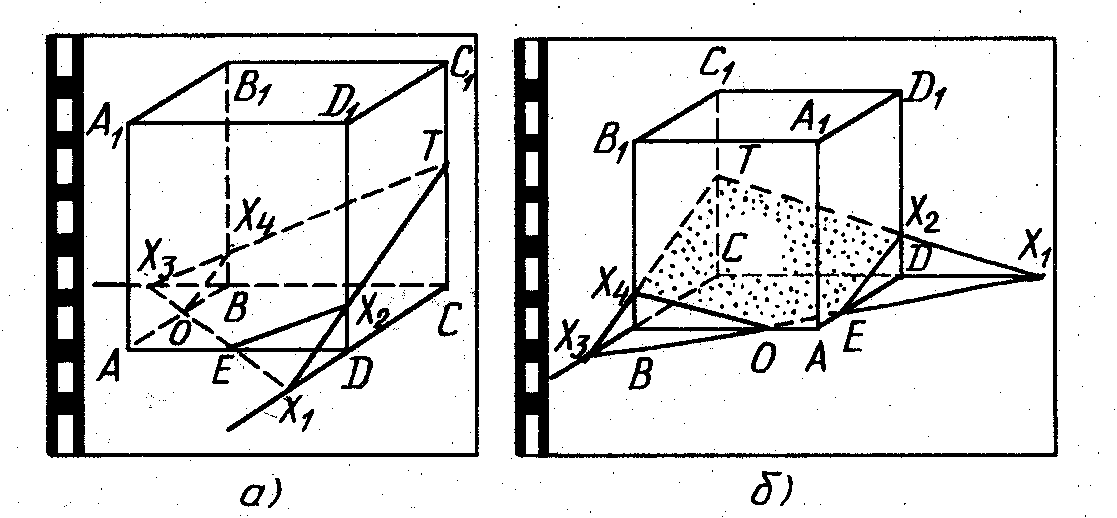



Задача 3. Постройте сечение куба плоскостью, проходящей через точки Т, К и О.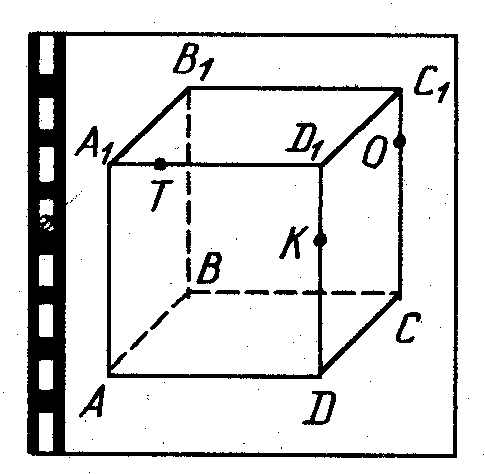

Метод внутреннего проектирования

Сущность этого способа заключается в следующем. Имея три точки, определяющие плоскость сечения, находят их проекции на основную плоскость, а также проекцию еще не построенной точки. По трем данным точкам и четырем проекциям отыскивают четвертую точку, принадлежащую плоскости сечения. Таким же образом, получают пятую, шестую и т.д. точки, принадлежащие поверхности геометрического тела и плоскости сечения, т.е. сечению.

Задача 3(задача 1, 2способ)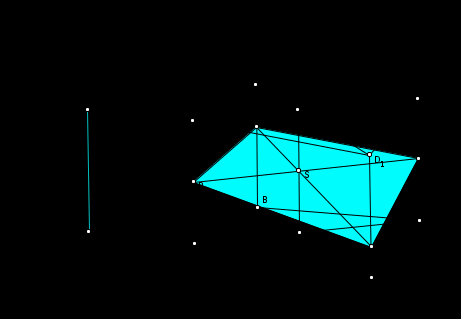

Анализ

Выберем направление внутреннего проектирования параллельно боковым ребрам призмы. За основную плоскость примем плоскость основания ABCD, Тогда проекциями точек P,K,M на основную плоскость будут точки A,D,C.Три точки P,K,M не лежат на одной прямой и поэтому определяют единственную плоскость. Чтобы построить сечение, достаточно определить точку встречи этой плоскости с четвертым ребром. Эту точку можно указать, если построить прямую, принадлежащую секущей плоскости и пересекающую ребро DD₁.Очевидно, эта прямая должна принадлежать какой-то плоскости, в которой расположена прямая DD₁. Две такие плоскости уже есть ADD₁A₁ и DCC₁D₁.В каждой из них имеется по одной точке, принадлежащей секущей плоскости. Но для проведения прямой нужны две точки. Построим диагональные плоскости. Получим линию пересечения ОО ₁ .

Прямая РМ пересечет ОО₁ в точке S.Точки К и S принадлежат плоскости сечения и плоскости BDD₁B₁.Эти две точки определяют прямую, которая, пересекаясь с DD₁ даст искомую точку.

Построение.

• 
  Строим РМ и ее проекцию А₁С₁.
  
• 
  Строим плоскость BDD₁B₁. B₁D₁ - проекция искомой прямой.
  
• 
  Точка О₁-проекция точки пересечения РМ с искомой прямой.
  
• 
  Проводим прямую через О ₁ параллельно ВВ₁.Получаем точку S.
  
• 
  Строим прямую КЕ.
  
• 
  Точка Т - искомая.
  

Доказательство

1. 
   Точки Р и М принадлежат плоскости сечения, отрезок РМ принадлежит плоскости сечения .Следовательно и точкаS принадлежит этой же плоскости.
   
2. 
   Точки К иS принадлежат искомой плоскости. Поэтому всякая точка прямой KS ,в том числе и точка Т ,принадлежит плоскости сечения.
   

Исследование

Решение всегда возможно и единственно. Поскольку точки Р, К, М не лежат на одной прямой, они определяют единственную плоскость.

Практические задания.

Предложенные задания взяты из “Живой геометрии”, которую можно использовать при наличии интерактивной доски или проектора с функцией интерактивной доски.

Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание 7
Задание 8
Задание 9

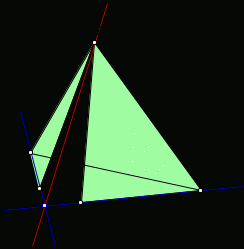
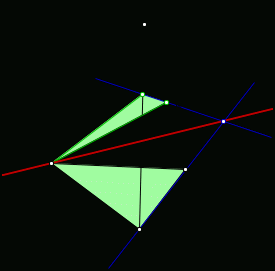
Задания на построение линий пересечения двух плоскостей

	1 способ 2 способ

Задания для построения сечений по темам.

Призма.

Список использованной литературы:

1. 
   Александров И. Геометрические задачи на построения и методы их решения. —М., 2006.
   
2. 
   Бескин Н.М. Изображение пространственных фигур — М., 1971.
   
3. 
   Василевский А.Б. Методы параллельных проекций. — Мн., 1985.
   
4. 
   Вотрогов В. Методы построения изображений.— Хабаровск, 1978.
   
5. 
   Гольдерберг Я.Е. С чего начинается решение стереометрической задачи.— Киев: «Радянська школа», 2010.
   
6. 
   Добровольская Н.А. «Творческие задачи на создание дополнительных построений» Изд. Рост.унив. 1984 .
   
7. 
   Изоак Д.Ф. О задачах на построение в стереометрии — М., 2018.
   
8. 
   Математика в школе. — 1990. —№3
   
9. 
   Математика: Приложение к газете «Первое сентября». — 2011—№29, 30, 31
   
10. 
    Орехов П.С. Изображения в стереометрии: Пособие для учителей. —Ижевск, 2016.
    
11. 
    Раневский К. Систематический курс геометрии и методы решения задач на построение — М.: Госиздат.1987.
    
12. 
    Саранцев Г.И. Решаем задачи на геометрические преобразования —М.,1997.
    
13. 
    Шарыгин В.Н. Решение задач по стереометрии.— М.,2000.
    

Электронные ресурсы.

1. 
   fio.novgorod.ru/projects/project2599/index.htm  
   
2. 
   Электронный учебник «Математика 5-11. Практикум»
   
3. 
   Виртуальная школа Кирилла и Мефодия. Уроки геометрии в 10 – 11-ых классах.