привод-оксана. Методические пособие

• Название: Методические пособие
• Дата: 04.04.2023
• Размер: 2.43 Mb.
• Имя файла: привод-оксана.doc
• Тип: Документы; #1035824
• страница: 20 из 21

38.Переходные процессы при пуске двигателя

1. Электромагнитные переходные процессы в обмотке возбуждения.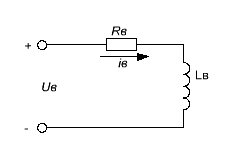




Исходное уравнение по II закону Кирхгофа:

; (1)


Рисунок 1
; (2)

;

;

Получаем:

; (3)

; ;

; (4)

Если , то:

; (5)

Во времени график нарастания тока возбуждения выглядит как на рисунке 2.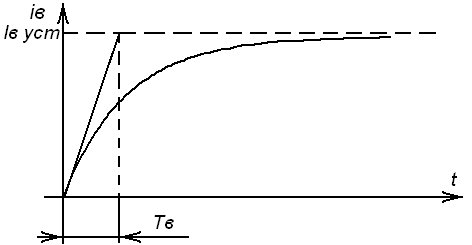



Рисунок 2
Влияние скорости возбуждения.
Чтобы форсировать изменение I в обмотке возбуждения генератора, надо:

1) параметрический способ за счет изменения параметров в цепи возбуждения генератора.

Добавим последовательно с обмоткой возбуждения добавочное сопротивление 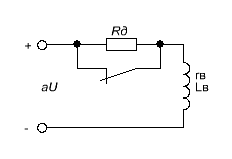(рисунок 3).



Рисунок 3

Новое значение постоянной времени примет вид:

;

И будет иметь вид изображенный на рисунке 4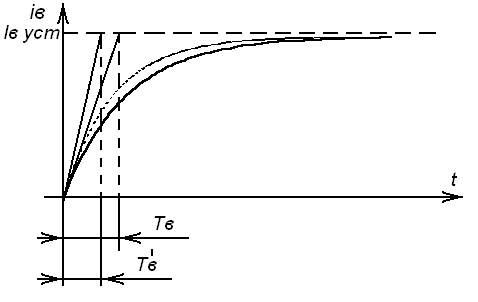



Рисунок 4
Значение коэффициента найдем из соотношения:

;

– коэффициент форсировки;

Но в этом случае чтобы Iв осталось неизменным, необходимо Uв увеличить в раз.

Уравнение (5) примет вид: . (6)

2) Форсировка отсечкой.

При данном способе форсируется подводимое напряжение к обмотке возбуждения в раз. В этом случае . Закон изменения тока в обмотке возбуждения в этом случае опишется уравнением:

(7)

Так как в этом случае установившееся значение тока превосходит допустимое в 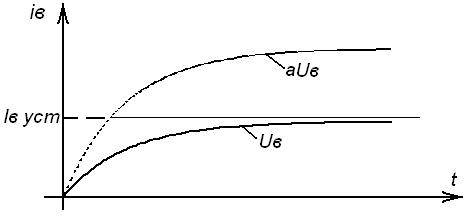раз, то по достижении током этого значения необходимо ограничить ток (отсечь). Этот способ называется форсировкой с отсечкой. Переходный процесс данного типа форсировки изображен на рисунке 5



Рисунок 5

Время переходного процесса вычисляется из (5) или (6) как:

(8)

График зависимости коэффициента форсировки от отношения времени переходного процесса к постоянной времени изображен на рисунке 6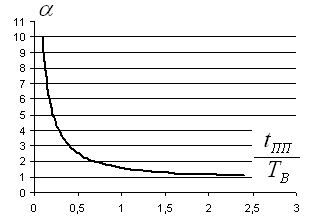



Рисунок 6

Из этого графика следует что больше чем (3÷4) принимать нецелесообразно, так как на практически не влияет.
2. Переходные процессы в двигатели постоянного тока независимого возбуждения.

Схема соединения двигателя изображена на рисунке 7.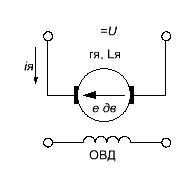



Рисунок 7
; (9)

; (10)

; (11)

;

;

(12)

(13)

Подставляя (13), (10) и (12) в (9) получим:

(14)

или (15)

Разделим обе части уравнения (15) на С:

(16)

Обозначим – электромагнитная постоянная времени.

Составляющую умножим на , получим:

,

где: – электромагнитная постоянная времени.

С учетом последнего выражения:

(17)

Уравнение (17) позволяет производить анализ поведения электродвигателя в переходных режимах.

В статическом (установившемся) режиме, при уравнение (17) будет выглядеть как:

(18)

– уравнение электромеханической характеристики, которая изображена на рисунке 8.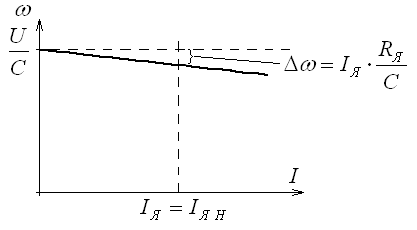



Рисунок 8
Переходные процессы будут вычисляться по выражению (рисунок 9):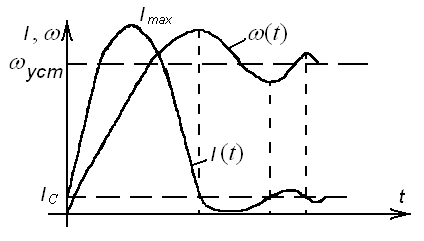




Рисунок 9
Здесь .

Если считать что , то решение дифференциального уравнения для двигателя можно заменить на:

;



Данные графики изображены на рисунке 10.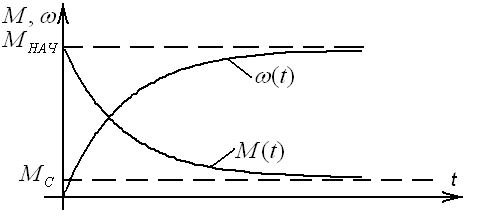


Рисунок 10
3. Переходные процессы в системе Г-Д.
Схема системы Г-Д изображена на рисунке 11.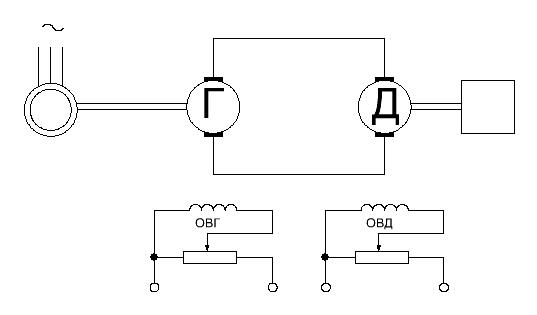



Рисунок 11
; (19)

; (20)

; (21)

; (22)

Из (21) ; (23)

; (24)

Подставив (23) и (24) в (20) получим

; (25)

или ; (26)

;

При , – можно принебречь, тогда

; (27)

Учитывая то что , из (27) определим:

; (28)

; (29)

Подставляя (28) и (29) в (26) получим: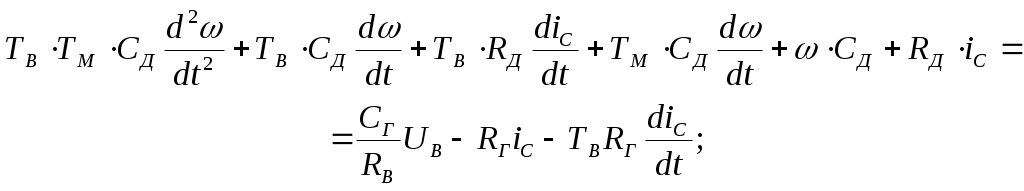

(30)

; (31)

Его характеристическое уравнение:





В установившемся режиме:

; (32)

или ;

где: .

Механическая характеристика (32) изображена на рисунке 12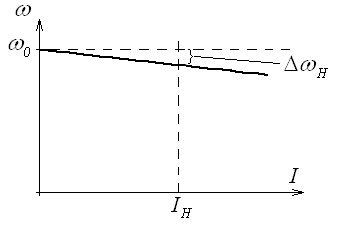



Рисунок 12
Полное решение уравнения (31) имеет вид:

. (33)