ИДЗ. ИДЗ №1_РЕШЕНИЕ ЗАДАЧ ГРАФИЧЕСКИМ СПОСОБОМ_заочная форма - копия.. Методические рекомендации для выполнения индивидуального домашнего задания использовать материалы учебного пособия Н. Л. Соловьевой Экстремальные модели менеджмента и экономики
 Скачать 83.13 Kb. Скачать 83.13 Kb.
|
|
Задание: 3. Механический цех может изготовить за смену 600 деталей №1 или 1200 деталей №2. Производственная мощность термического цеха, куда эти детали в тот же день поступают на термообработку, позволяет обработать за смену 1200 деталей №1 или 800 деталей №2. Цены на детали одинаковые. Определить ежедневную производственную программу выпуска деталей, максимизирующую стоимость товарной продукции, при условии, что мехнический цех работает в три смены, а термический – в две. Составить математическую модель задачи и найти решение графическим методом. Задачи размещены в Приложении В и в учебном пособии В.И. Муравьев, С.А. Тавридович, А.А. Брацлавский, Н.Л. Соловьева «Модели и методы оптимизации в экономике и менеджменте». Оформление индивидуального домашнего задания: Методические рекомендации: для выполнения индивидуального домашнего задания использовать материалы учебного пособия Н.Л. Соловьевой «Экстремальные модели менеджмента и экономики» п. 2.3 стр. 25 Пример решения Имеется два вида полуфабрикатов: сплав А и сплав В, каждый из которых состоит из меди, олова и цинка, входящих в них в следующих пропорциях: 1:1:8 и 1:3:6 соответственно. На предприятии получают новый сплав, состоящий из сплавов А и В. Новый сплав должен содержать не более 2 кг меди, не менее 3 кг олова, а содержание цинка должно составлять от 7,2 кг до 12,8 кг. Стоимость 1 кг каждого полуфабриката (сплава А, сплава В) составляет 4 у.е. и 6 у.е. соответственно. Определить количество каждого полуфабриката, обеспечивающее получение нового сплава с минимальными затратами на сырье. Меди было закуплено 2 кг, олова – 3 кг, цинка 12,8 кг. Закупочная и продажная цена одного килограмма сырья одинакова и составляет: меди - 2 у.е., олова – 6 у.е., цинка – 4 у.е. Решение: Составим математическую модель задачи. Для этого запишем условие задачи в табличном виде (таблица 1). Таблица 1 – Условие задачи
Цель задачи заключается в минимизации затрат на сырье. Затраты на сырье можно определить по следующей формуле: 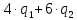 , ,где  объем закупки каждого полуфабриката, требуемых для получения нового сплава. объем закупки каждого полуфабриката, требуемых для получения нового сплава. Пусть  объем закупки объем закупки 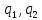 (кг) каждого полуфабриката, тогда целевая функция задачи будет следующей: (кг) каждого полуфабриката, тогда целевая функция задачи будет следующей: 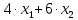 . .Цель задачи: 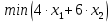 Ограничения задачи продиктованы содержанием сырья в новом сплаве (таблица 1). Всего меди для нового сплава потребуется: 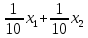 ; олова - ; олова - 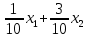 и цинка - и цинка - 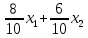 . .Тогда технологические ограничения задачи будут следующими: 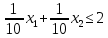 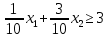 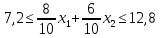 Кроме технологических ограничений следует наложить ограничения на переменные:  . .Тогда математическая модель задачи будет следующей: 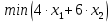   Решим полученную математическую модель графическим методом. Для решения задачи графическим методом следует построить область допустимых решений задачи, заданную технологическими ограничениями и ограничениями на переменные. Выполним построение в декартовой системе координат  . .Определим область допустимых значений (рисунок 1).  Рисунок 1 – Область допустимых значений Построим вектор-градиент целевой функции, имеющий координаты  В заданных отрезках на осях проще построить вектор, коллинеарных градиенту с координатами  и определим положение линии уровня, проходящую через вершину области допустимых решений в направлении вектора-антиградиента целевой функции (рисунок 2). и определим положение линии уровня, проходящую через вершину области допустимых решений в направлении вектора-антиградиента целевой функции (рисунок 2).  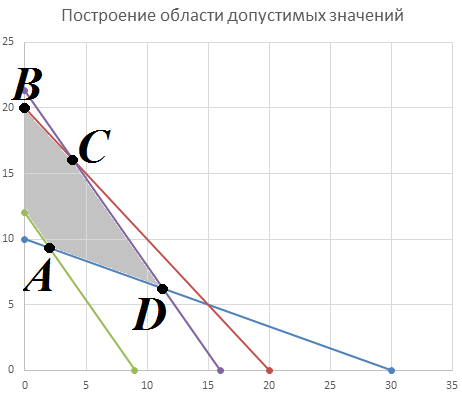 Рисунок 2 – Определение минимального значения целевой функции Очевидно, что точкой минимума целевой функции является точка А, лежащая в пересечении прямых, заданных уравнениями: 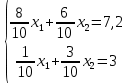 Определим координаты точки А, решив эту систему уравнений. 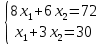 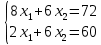 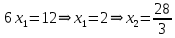 Значение целевой функции при найденных значениях переменных будет равно: 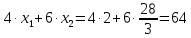 Ответ: оптимальный объем закупки полуфабрикатов составит 2 кг и 9,33 кг, а минимальные затраты на сырье – 64 у.ед. или 64(2;9,33) | ||||||||||||||||||||||||||||||
