Методические рекомендации. Методические рекомендации к выполнению лабораторной работы Численное решение уравнений

• Название: Методические рекомендации к выполнению лабораторной работы Численное решение уравнений
• Анкор: Методические рекомендации
• Дата: 06.05.2022
• Размер: 67.83 Kb.
• Имя файла: Методические рекомендации.docx
• Тип: Методические рекомендации; #515472
• страница: 3 из 5

Метод итераций

^{Приведем уравнение f(x)=0 к виду} x  (x) ^{. Тогда рекуррентная формула}

^x_n1 ^{ (x}_n ^), n  0,1,... ^{. Для сходимости процесса итерации необходимо, чтобы}

'(x)  1,

^при x [a;b] ^{. Если '(x)  1, то сходимость не обеспечена.}

В случае, когда свободный хвыразить не удается, целесообразно воспользоваться следующим приемом, позволяющим обеспечить выполнение условий сходимости.

^{Построим функцию} (x)  λf(x)  x, ^{где параметр λ может быть определен по}

,
^{правилу:если} f^(x)  0,^то  ¹  λ  0; ^если f^(x)  0, ^то 0  λ  ¹

где

r r

r  max( f^(a) ; f^(b) ) .

x[a;b]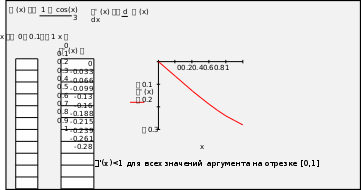

Приведем уравнение f(x)=0к виду x = (cos(x)+1)/3и проведем исследование.


Выберем начальное значение (в методе итерацийx₀– произвольное значение из отрезка [a;b]), например, x₀=0, и с использованием итерационной функции φ(x)  (cos(x)  1) / 3 ^{выполним три итерации.}

2. «Ручной расчет» трех итераций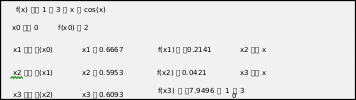

Результаты вычислений удобно представить в виде табл. 1.2.

к	Xк	f(xк)
0	0	2
1	0.6667	-0.2141
2	0.5953	4.21 • 10-2
3	0.6093	-7.9496• 10-3

3. Погрешность численного решения нелинейных уравнений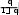

Погрешность результата, вычисленного методом итерации, можно оценить с помощью выражения:

x * x₃ 

x₃  x₂

 ^0.28  0.014  0.0054 ^.

0.72

3. Схема алгоритмов, программа и контрольное тестирование

Построить базовую схему алгоритма метода половинного деления и написать программу самостоятельно, провести контрольное тестирование.

3. Результаты «расчета на ПК»

Результаты расчета приближенного корня уравнения с различной точностью, по программе, написанной по схеме алгоритма с различными значениями точности, приведены в следующей таблице:

E	n	x	f(x)
0. 01	4	0.606	4.93E-03
0. 001	5	0.6069	5.302E-04
0.0001	6	0.60708	5.6925E-05

3. Зависимость числа итераций от точности в логарифмическом масштабе

Для метода итерации по данным таблицы построим зависимость n(E)

ε	0.01	0.001	0.0001
n	4	5	6