Методические рекомендации. Методические рекомендации к выполнению лабораторной работы Численное решение уравнений
 Скачать 67.83 Kb. Скачать 67.83 Kb.
|
Метод НьютонаИсследование задания для «ручного расчета»Из условия для уравнения 1- 3х + cos(x) = 0, где f(0) f(x) 0 , а f(1) f(x) 0 выберем начальное приближение к корню: x0 1. Для получения решения уравнения методом Ньютона воспользуемся следующей рекуррентной формулой: xn1 xn f(xn ) . f '(xn ) В нашем случае x n1 xn 1 3xn cos xn . 3 sin x n «Ручной расчет» трех итераций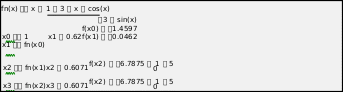 Представим вычисления в виде следующей табл. 1.2.
Погрешность численного решения нелинейных уравненийОценку погрешности результата, вычисленного методом Ньютона, можно проводить по формуле: x * x M2 (x x )2. 1 n 2m n n1 Оценим погрешность после трех итераций: * M (x x )2 m1 f(0) 3, M2 f(0) 1, x x3 2 3 2 . 2m Тогда x* x 1 3 0.000002 . Схема алгоритмов, программа и контрольное тестированиеПостроить базовую схему алгоритма метода половинного деления и написать программу самостоятельно, провести контрольное тестирование. Результаты «расчета на ПК»Результаты расчета приближенного корня уравнения с различной точностью по программе, написанной по схеме алгоритма с различными значениями точности, приведены в следующей таблице:
Зависимость числа итераций от точности в логарифмическом масштабеДля метода Ньютона деления по данным таблицы построим зависимость n(lgE)
|
