Методические рекомендации. Методические рекомендации к выполнению лабораторной работы Численное решение уравнений

• Название: Методические рекомендации к выполнению лабораторной работы Численное решение уравнений
• Анкор: Методические рекомендации
• Дата: 06.05.2022
• Размер: 67.83 Kb.
• Имя файла: Методические рекомендации.docx
• Тип: Методические рекомендации; #515472
• страница: 2 из 5

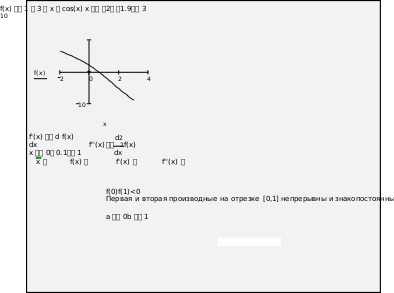
Пример выполнения задания

1. Задание для решения нелинейных уравнений:

   • 
     ^{уравнение} f(x)  1 3x  cos x  0 ^;
     
   • 
     методы решения нелинейных уравнений для ручного расчета – половинного деления, итерации, Ньютона и хорд;
     
   • 
     методы решения нелинейных уравнений для расчета на ПК – половинного деления, итерации, Ньютона и хорд.
     

2. Отделение корней (графический и аналитический методы)

0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1

2
1.695
1.38
1.055
0.721
0.378
0.025
-0.335
-0.703
-1.078
-1.46

-3
-3.1
-3.199
-3.296
-3.389
-3.479
-3.565
-3.644
-3.717
-3.783
-3.841

-1
-0.995
-0.98
-0.955
-0.921
-0.878
-0.825
-0.765
-0.697
-0.622
-0.54

Следовательно, 1 - 3х + cos(x) = 0 имеет единственный корень на отрезке [0;1].
Методполовинногоделения

1. Исследование задания

Метод половинного деления сходится, если на выбранном отрезке отделен один корень. ^{Так как на отрезке [0;1] функция} f(x)  1 3x  cos x  0 ^{меняет знак (} f(0)  f(1)  0 ^{) и} монотонна (f’(x)<0), то условие сходимости выполняется.

^{Начальным приближением является середина отрезка [0;1]:} x₀

 ^{a  b =0.5.}

2

2. Результаты «ручного расчета» трех итераций

Результаты вычислений представить в виде табл. 1.1

n	a	b	f(a)	f(b)	(a+b)/2	f( (a+b)/2)	b-a
1	0	1	2	-1.459	0.5	0.377	0.5
2	0.5	1	0.377	-1.459	0.75	-0.518	0.25
3	0.5	0.75	0.377	-0.518	0.625	-0.064	0.125
4	0.5	0.625	0.377	-0.064	0.563	0.158	0.063

После трех итераций приближение к корню x₃=0.563.

3. Погрешность численного решения нелинейных уравнений

Оценим погрешность результата, полученного после 3-х итераций

b₃  a₃

 0.125 ^.

4. Схема алгоритмов, программа и контрольное тестирование

Построить базовую схему алгоритма метода половинного деления и написать программу самостоятельно, провести контрольное тестирование.

5. Результаты «расчета на ПК»

Результаты расчета приближенного корня уравнения с различной точностью по программе, написанной по схеме алгоритма с различными значениями точности, приведены в следующей таблице:

E	n	x	f(x)
0. 01	7	0.605	5.8E-03
0. 001	10	0.6069	6.0E-04
0.0001	14	0.60709	5.5E-05

6. Погрешность результата «расчета на ПК»

Абсолютные погрешности результатов, полученных при различных заданных значениях точности расчета с использованием «расчета на ПК», относительно значения корня, вычисленного с использованием математических пакетов (x*=0.607102), равны:

ε	Погрешность
0.01	0.0021
0.001	0.0002
0.0001	0.00001

7. Зависимость числа итераций от точности в логарифмическом масштабе

Для метода половинного деления по данным таблицы построим зависимость n(lgE)

ε	0.01	0.001	0.0001
n	7	10	14

1. 
   Исследование задания