Методические рекомендации по использованию составленной системы задач
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
Пример краткого содержания урока. Учебник Н.Я. Виленкин и др. 5 класс. Тема урока «Сложение натуральных чисел и его свойства» 2 урок по этой теме из 4 уроков по традиционной программе. Цель урока: Повторить свойства сложения натуральных чисел; учить применять свойства сложения при устных вычислениях; продолжить работу с текстовыми задачами. Ход урока: . Организационный момент. . Устный счет. . Сообщение темы урока. . Работа по теме урока. . Работа над нестандартными задачами: А) Какие цифры? Догадайтесь, какие цифры в выражении заменены буквами А, В, С: АА + А = А6. (Цифра 3). 4В + В = В0. (Цифра 5). СС + С = С2. (Цифра 1). Б) Из семи цифр. Пусть записано подряд семь цифр от 1 до 7: . Легко соединить их знаками “плюс” и “минус” так, чтобы получилось 40: + 34-5 + 6-7 = 40 Попробуйте найти другие расстановки знаков между теми же цифрами, при которых получилось бы не 40, а 55. ( + 4-5-67 = 55; 1-2-3-4 + 56 + 7 = 55; 12- 3 + 45 -6 + 7 = 55, Возможно, учащиеся смогут найти и другие варианты ответов). 6. Повторение изученного материала. . Самостоятельная работа. . Подведение итогов урока. Методические рекомендации. В ходе изучения этой темы учащиеся должны усвоить основные способы решения нестандартных задач способом сложения. Решение задачи, разобранной на занятиях, представляет собой метод решения большого класса задач. Эти методы повторяются и углубляются при решении последующих задач. В каждом уроке разбираются задачи разного уровня сложности. От простых, повторяющих школьную программу задач (таких немного), до сложных задач, решение которых обеспечивает хорошую и отличную оценку на математических олимпиадах. Тема урока: «Больше или меньше» Цель урока: Учить сравнивать натуральные числа и записывать результаты сравнения виде неравенства, определять место натурального числа на координатном луче. . Организационный момент. . Устный счет. . Сообщение темы урока. . Работа по теме урока. . Повторение изученного материала. . Работа над нестандартными задачами: А) Число 66. Число 66 надо увеличить в полтора раза, не производя над ним никаких арифметических действий. Как это сделать? (Нужно написанное число 66 перевернуть “вверх ногами”). Б) Кошки и котята. Четыре кошки и 3 котенка весят 15 килограммов, а 3 кошки и 4 котенка весят 13 килограммов. Предполагается, что все взрослые кошки весят одинаково и котята также весят одинаково. Сколько весит каждая кошка и каждый котенок в отдельности? (Кошка весит 3 килограмма, котенок - 1 килограмм). 7. Самостоятельная работа. . Подведение итогов урока. Методические рекомендации. В ходе изучения этой темы учащиеся должны усвоить основные способы решения нестандартных задач способом 2.2 Описание и результаты экспериментальной работы Для подтверждения гипотезы и выполнения поставленных задач была проведена экспериментальная работа, которая проходила в три этапа: констатирующий, формирующий и контролирующий. Цель исследования: убедится в эффективности использования системы нестандартных задач для развития логического мышления учащихся 5-6 классов. В эксперименте приняли участие учащиеся 5 классов в количестве 17 человек. 5 «А класс в количестве 9 человек представлял контрольную группу учащихся, а 5 «Б» класс в количестве 8 человек - экспериментальную. Констатирующий этап: На этом этапе экспериментальной работы провела анкетирование и тестирование учащихся 5 и 6 классов. Участвовало в 5 классах 9 учащихся, в 6 классе 8 учащихся. Также провела самостоятельную работу, беседовала с учителями и учащимися. Для определения уровня развития логического мышления учащихся использовались методики: «Четвёртый лишний» с использованием картинок, серия заданий на определение уровня сформированности логического мышления. А также Методика «Числовые ряды». Цель данной методики: исследование логического аспекта математического мышления. Методика 1 «Четвёртый лишний». По методике «Четвертый лишний» ребёнку показывали четыре картинки, три из которых связаны между собой по смыслу, а одно изображение не подходит к остальным. Ребёнку предлагается найти «лишнюю» картинку и объяснить, почему она «лишняя».тимульный материал: 7 карточек с четырьмя изображениями, одно из которых лишнее: стол, кровать, пол, шкаф; молоко, сливки, сало, сметана; ботинки, сапоги, шнурки, валенки; молоток, топор, пила, гвоздь; трамвай, автобус, трактор, троллейбус; берёза, сосна, дерево, дуб; самолёт, телега, человек, корабль. Инструкция: «Посмотри на эти картинки». Одно из изображений здесь лишнее, оно не связано с остальными рисунками. Подумай, какое это изображение и назови его. Объясни почему?» Ход проведения. В первом задании нужно добиться от ребёнка правильного ответа. Оно не оценивается. В процессе тестирования ребёнку последовательно предъявляются все 7 карточек. Помощь взрослого заключается только в дополнительных вопросах типа: «Хорошо ли ты подумал?», «Ты уверен, что выбрал правильное слово?», но не в прямых подсказках. Если ребёнок после такого вопроса исправляет свою ошибку, ответ считается правильным. Анализ результатов. За каждый правильный ответ начисляется 1 балл, за неправильный - 0 баллов. -8 баллов - высокий уровень развития логического мышления; -5 баллов - средний уровень развития логического мышления; и менее баллов - логическое мышление развито слабо. После проведения данной методики были получены следующие результаты (Таблица 1). Таблица 1. Уровень сформированности логического мышления школьников классов
Для наглядности представим результаты констатирующего этапа эксперимента на рисунке 1. 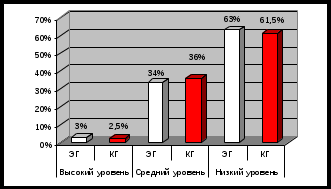 Рис.1 Уровни сформированности логического мышления школьников средних классов на констатирующем этапе эксперимента. Методика 2 «Числовые ряды». Инструкция: Внимательно прочитай каждый ряд чисел и на два свободных места напиши такие два числа, которые продолжат данный числовой ряд. Например: 4 6 8 10 12 14 16 10 9 3 7 6 5 4 3 2 3 3 4 4 5 5 6 6 3 1 7 2 7 3 7 4 7 Результаты оценивались по количеству ошибок. На основе данной методики были определены следующие уровни развития логического мышления: -1 ошибка: высокий уровень; -5 ошибок: средний уровень; <5 ошибок: низкий уровень.
Проведение констатирующего этапа способствовало делению школьников средних классов на группы по уровням: в экспериментальной группе 63% школьников имели низкий уровень логического мышления, 34% - средний и 3% - высокий. В контрольной группе 61,5% школьников имели низкий уровень логического мышления, 36% - средний и 2,5% - высокий. Из данных результатов можно сделать следующий вывод, что школьники опираются не на систему признаков, указанную в определении, а лишь на отдельные признаки. В то же время определение этих понятий они знают. Следовательно, учащиеся определение запомнили, но работать с ним не научились. Причина всех этих ошибок - неумение применить логический прием подведения под понятие. Учащиеся допускают еще больше ошибок при выполнении классификаций, при выведении следствий из данных посылок. В то же время, как показывают исследования, многие из этих приемов учащиеся могут успешно усвоить уже в начальной школе, если работу вести планомерно и целенаправленно. В классах, где мы проводили эксперимент, имеются большие перспективы для работы по развитию логического мышления. Следовательно, результаты констатирующего этапа исследования требуют проведения формирующего этапа эксперимента в соответствии с предложенной гипотезой. Формирующий этап: В формирующем эксперименте приняли участие учащиеся экспериментальной группы. На данном этапе эксперимента мы провели работу по развитию логического мышления у школьников средних классов. Развитие логического мышления при изучении математики состоит, в формировании у учащихся характерных для этого предмета приемов мыслительной деятельности. При этом важно, чтобы в структуру умственной деятельности школьников помимо алгоритмических умений и навыков, фиксированных в стандартных правилах, формулах и способах действий, вошли эвристические приемы, которые необходимы для решения творческих задач, применение знаний в новых ситуациях, доказательства высказываемых утверждений. Процесс обучения предполагает целенаправленное управление мыслительной деятельностью учащихся, что приводит к продвижению учеников в их умственном развитии. Чтобы развить мышление учащихся, нужно показать им как функционирует мышление на практике. Развитие происходит в деятельности, поэтому необходимо создавать ученикам условия соответствующей деятельности, нужно демонстрировать сложную картину поиска решения, всю трудность этой работы. В этом случае ученики становятся активными участниками процесса поиска решения, начинают понимать источники возникновения решения. Как результат - ими легче осваиваются причины ошибок, затруднений, оценивается найденный способ решения и ход логических мыслей, а без этого знания не могут перейти в убеждения. Системное развитие логического мышления должно быть неотрывно от урока, каждый ученик должен принимать участие в процессе решения не только стандартных заданий, но и нестандартных задач развивающего характера (активно или пассивно). На уроках учитель должен моделировать ту умственную деятельность, которая нужна на данном этапе развития (учить анализировать задачи, делать чертежи, выявлять отношения объектов и т.д.). Это имеет обучающее и воспитывающее значение: учащиеся приобщаются к методу поиска, ориентируются не только на результат, но и на процесс его достижения, т.е. учатся мыслить логически. Можно выделить два подхода к формированию и становлению логического мышления: . Традиционное обучение, приводящее в зависимости от воздействия и других объективных причин к формированию либо эмпирического, либо теоретического мышления. . Специально организованное обучение, ориентированное на формирование учебной деятельности, приводящее к становлению теоретического мышления. Для формирования логического мышления приоритетным является второй подход, который и был положен в основу формирования технологии. Для осуществления формирования логического мышления учащихся 5 классов была составлена система нестандартных задач: комбинаторные задачи, логические квадраты, геометрические задачи, задачи на смекалку, задачи на переливание. Эти нестандартные задачи можно разделить на группы, учитывая их воздействие на мыслительную деятельность учащихся. Формирование гибкости ума, освобождение мышления от шаблонов происходит при решении задач на смекалку т.к. в большинстве своем эти задачи не привязаны к темам и не требуют особой теоретической подготовки. Задачи на переливание, логические квадраты, учат школьников умению рассуждать, формируют математический стиль мышления, развивают логико-лингвистические способности детей, которые приводят к умению четко мыслить, полноценно логически рассуждать и ясно излагать свои мысли. Комбинаторные задачи используются для формирования умений поиска решения задач, интуиции, требуют знания теории и нешаблонного подхода к решению. Задачи с геометрическим содержанием нацелены на знание геометрических фигур и их свойств как основы для формирования пространственных и изобразительных умений школьников, на расширение кругозора. Учитель, преподающий в 5-6 классах, может развивать логическое мышление учащихся с помощью созданной системы нестандартных задач. Для этого необходимо учитывать следующее: . Выбранные нестандартные задачи должны быть посильными для детей; . Нестандартные задачи, отобранные для одного урока, должны быть разнообразными для воздействия на различные компоненты мышления; . Если ученики не справляются с нестандартными задачами, то целесообразно оставить его на обдумывание до следующего урока; . Ученикам можно дать необязательное домашнее задание по составлению аналогичных задач; Результативность системы нестандартных задач является средством повышения уровня логического мышления учащихся 5 классов, развивает интеллект. Повышается успеваемость учащихся, прививается интерес к предмету. Данная система нестандартных задач составлена для учителей преподающих в 5-6 классах. Устойчивые положительные результаты можно получить при выполнении методических рекомендаций к данной системе нестандартных задач. Доказательством результативности опытно-экспериментальной работы по целенаправленному развитию логического мышления у школьников 5 классов явились данные контрольного этапа, который заключался в определении уровней сформированности логического мышления в целом (табл. 2), проведенного по тем же методикам, которые использовались в начале опытно-экспериментальной работы. Таблица 2 Уровень развития логического мышления (до и после проведения эксперимента)
Для наглядности представим результаты контрольного этапа эксперимента на рисунке 2. 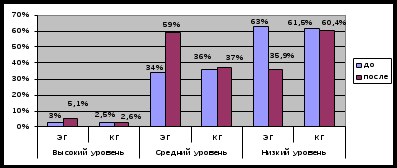 Рис.2 Результаты контрольного этапа эксперимента Сравнивая результаты исследований, мы отмечаем значительные изменения. Больший процент школьников в экспериментальной группе стал обладать высоким уровнем логического мышления. Но в контрольной группе эти изменения незначительны, так как не учитывались психологические условия и средства формирования логического мышления. Как показывают данные таблицы, процент школьников в экспериментальной группе, имеющих низкий уровень логического мышления снизился на 27,1 %, средний уровень стал характерен для 59 % испытуемых, что на 25 % больше, чем на констатирующем этапе эксперимента. На 2,1 % увеличилось число школьников, обладающих высоким уровнем логического мышления. Вывод: проведенный анализ подтвердил эффективность предлагаемой системы нестандартных задач, обеспечившей более высокий уровень развития логического мышления у школьников средних классов, показал эффективность использованных нами средств развития логического мышления учащихся среднего школьного возраста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
