Методические рекомендации по использованию составленной системы задач

• Название: Методические рекомендации по использованию составленной системы задач
• Дата: 25.04.2023
• Размер: 0.65 Mb.
• Имя файла: bibliofond.ru_784256.rtf
• Тип: Методические рекомендации; #1087380
• страница: 2 из 4

Глава 2. Применение нестандартных задач на уроках математики 5-6 классах для развития логического мышления
2.1 Построение системы нестандартных задач, направленных на развитие логического мышления учащихся 5-6 классов
Математику любят в основном те ученики, которые умеют решать задачи. Следовательно, научив детей владеть умением решать нестандартные задачи, мы окажем существенное влияние на их интерес к предмету, на развитие логического мышления и речи. Кроме того, они являются мощным средством активизации познавательной деятельности, т. е. вызывают у детей огромный интерес и желание работать.

1. Задачи на смекалку.

1.1. Масса цапли, стоящей на одной ноге 12 кг. Сколько будет весить цапля, если встанет на 2 ноги?

1.2. Пара лошадей пробежала 40 км. Сколько пробежала каждая лошадь?

.3. У семи братьев по одной сестре. Сколько всего детей в семье?

.4. Шесть котов за шесть минут съедают шесть мышей. Сколько понадобится котов, чтобы за сто минут съесть сто мышей?

.5. Стоят 6 стаканов, 3 с водой, 3 пустых. Как расставить их, чтобы стаканы с водой и пустые чередовались? Разрешается переставить только один стакан.
Рис. 1.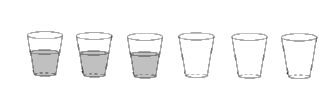



1.6. Геологи нашли 7 камней. Масса каждого камня: 1 кг, 2 кг, 3 кг, 4 кг, 5 кг, 6 кг и 7 кг. Эти камни разложили в 4 рюкзака так, что в каждом рюкзаке масса камней оказалась одинаковой. Как это сделали?

1.7. В классе причесанных девочек столько же, сколько непричесанных мальчиков. Кого в классе больше, девочек или непричесанных учеников?

.8. Летели утки: одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько всего летело уток?

.9. Миша говорит: «Позавчера мне было10 лет, а в следующем году мне исполнится 13 лет». Возможно ли это?

.10. У Андрея и Бори 11 конфет, у Бори и Вовы 13 конфет, а у Андрея и Вовы - 12. Сколько всего конфет у мальчиков?

.11. Отец с двумя сыновьями катались на велосипедах: двухколесных и трехколесных. Всего у них было 7 колес. Сколько было велосипедов, и каких?

.12. Во дворе куры и поросята. У них у всех 5 голов и 14 ног. Сколько кур и сколько поросят?

.13. По двору гуляют куры и кролики. Всего у них 12 ног. Сколько кур и сколько кроликов?

.14. У каждого марсианина по 3 руки. Могут ли 13 марсиан взяться за руки так, чтобы не оставалось свободных рук?

.15. Играя, каждая из трех девочек - Катя, Галя, Оля - спрятали одну из игрушек - медведя, зайца и слона. Катя не прятала зайца, Оля не прятала ни зайца, ни медведя. Кто какую игрушку спрятал?

2. Занимательные задачи.

2.1. Как расставить 6 стульев у 4 стен, чтобы у каждой стены было по 2 стула.

2.2. Папа с двумя сыновьями отправился в поход. На их пути встретилась река. У берега плот. Он выдерживает на воде одного папу или двух сыновей. Как переправиться на другой берег папе с сыновьями?

.3. Для одной лошади и двух коров выдают ежедневно 34 кг сена, а для двух лошадей и одной коровы -35кг сена. Сколько сена выдают ежедневно одной лошади и сколько одной корове?

.4. Четыре утенка и пять гусят весят 4кг100г, а пять утят и четыре гусенка весят 4кг. Сколько весят один утенок?

.5. У мальчика было 22 монеты - пятирублевые и десятирублевые, всего на сумму 150 рублей. Сколько было пятирублевых и десятирублевых монет?

.6. В квартире № 1, 2, 3 живут три котенка: белый, черный и рыжий. В квартире № 1 и 2 жил не черный котенок. Белый котенок жил не в квартире № 1. В какой квартире жил каждый из котят?

.7. За пять недель пират Ерема способен выпить бочку рома. А у пирата Емели ушло б на это две недели. За сколько дней прикончат ром пираты, действуя вдвоем?

.8. Лошадь съедает воз сена за месяц, коза - за два месяца, овца - за три месяца. За какое время лошадь, коза, овца вместе съедят такой же воз сена?

.9. Двое очистили 400 картофелин; один очищал 3 штуки в минуту, другой -2. Второй работал на 25 минут больше, чем первый. Сколько времени работал каждый?

.10. Среди футбольных мячей красный мяч тяжелее коричневого, а коричневый тяжелее зеленого. Какой мяч тяжелее: зеленый или красный?

.11. Три кренделя, пять коврижек и шесть баранок стоят вместе 24 рубля. Что дороже: крендель или баранка?

.12. Как тремя взвешиваниями на чашечных весах без гирь найти одну фальшивую (более легкую) монету из 20 монет?

.13. Из верхнего угла комнаты вниз по стене поползли две мухи. Спустившись до полу, они поползли обратно. Первая муха ползла в оба конца с одинаковой скоростью, а вторая, хоть и поднималась вдвое медленнее первой, но зато спускалась вдвое быстрее ее. Какая из мух раньше приползет обратно?

.14. В клетке находятся фазаны и кролики. У всех животных 35 голов и 94 ноги. Сколько в клетке кроликов и сколько фазанов?

.15. Говорят, что на вопрос о том, сколько у него учеников, древнегреческий математик Пифагор ответил так: «Половина моих учеников изучает математику, четвертая часть изучает природу, седьмая часть проводит время в молчаливом размышлении, остальная часть составляют 3 девы» Сколько учеников было у Пифагора?

3. Геометрические задачи.

3.1. Раздели пирог прямоугольной формы двумя разрезами на части так, чтобы они имели треугольную форму. Сколько получилось частей?

.2. Нарисуй фигуру, не отрывая кончика карандаша от бумаги и не проводя дважды один и тот же отрезок.

.3. Разрежь квадрат на 4 части и сложи из них 2 квадрата. Как это сделать?


.4. Убери 4 палочки так, чтобы осталось 5 квадратов.

.5. Разрежьте треугольник на два треугольника, четырехугольник и пятиугольник, проведя две прямые линии.

.6. Можно ли квадрат разделить на 5 частей и собрать восьмиугольник?

4. Логические квадраты.

4.1. Заполни квадрат (4 _х 4) числами 1, 2, 3, 6 так, чтобы сумма чисел по всем строкам, столбцами и диагоналям была одинаковой. Числа в строках, столбцах и диагоналях не должны повторяться.

4.2. Раскрась квадрат красным, зеленым, желтым и синим цветами так, чтобы цвета в строках, столбцах и по диагоналям не повторялись.

красный			желтый
	зеленый
			синий

4.3. В квадрате нужно разместить еще числа 2,2,2,3,3,3 так, чтобы по всем линиям получить в сумме число 6.

.4. Числа 3,4,5,6,8,9 расставить в клетках квадрата так, чтобы в любом направлении в сумме получить 21.

10
	7
	11

4.5.

4.6. В клетках квадрата поставить числа 4,6,7,9,10,11,12 так, чтобы в столбцах, в строчках и по диагоналям получить сумму 24.

	8
		5

5. Комбинаторные задачи.

5.1. У Даши 2 юбки: красная и синяя, и 2 блузки: в полоску и в горошек. Сколько разных нарядов у Даши?

5.2. Сколько существует двузначных чисел, у которых все цифры нечетные?

.3. Родители приобрели путевку в Грецию. До Греции можно добраться, используя один из трех видов транспорта: самолет, теплоход или автобус. Составьте все возможные варианты использования данных видов транспорта.

.4. Сколько разных слов можно образовать при помощи букв слова «соединение»?

.5. Из цифр 1, 3, 5 составить различные трехзначные числа так, чтобы в числе не было одинаковых цифр.

.6. Встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что один из нас блондин, другой брюнет, а третий рыжеволосый. Но ни у одного нет волос того цвета, на который указывает его фамилия», - заметил брюнет. «Ты прав», - сказал Белов. Какой цвет волос у художника?

.7. Три подруги вышли погулять в белом, зеленом и синем платьях и туфлях таких же цветов. Известно, что только у Ани цвет платья и цвет туфель совпадают. Ни туфли, ни платье Вали не были белыми. Наташа была в зеленых туфлях. Определите цвет платья и туфель на каждой из подруг.

.8. В отделении банка работают кассир, контролер и заведующий. Их фамилии Борисов, Иванов и Сидоров. Кассир не имеет ни братьев, ни сестер и меньше всех ростом. Сидоров женат на сестре Борисова и ростом выше контролера. Назовите фамилии контролера и заведующего.

.9. Для пикника сладкоежка Маша взяла в трех одинаковых коробках конфеты, печенье и торт. На коробках были этикетки: «Конфеты», «Печенье», и «Торт». Но Маша знала, что мама любит шутить и всегда кладет продукты в коробки, надписи на которых не соответствуют их содержимому. Маша была уверена, что конфеты не лежат в коробке, на которой написано «Торт». В какой же коробке торт?

.10. По кругу сидят Иванов, Петров, Марков, Карпов. Их имена Андрей, Сергей, Тимофей, Алексей. Известно, Иванов не Андрей и не Алексей. Сергей сидит между Марковым и Тимофеем. Петров сидит между Карповым и Андреем. Как зовут Иванова, Петрова, Маркова и Карпова?

6. Задачи на переливание.

6.1. Можно ли, имея лишь два сосуда емкостью 3 и 5л, набрать из водопроводного крана 4 л воды?

.2. Как разделить поровну между двумя семьями 12 л хлебного кваса, находящегося в двенадцатилитровом сосуде, воспользовавшись для этого двумя пустыми сосудами: восьмилитровым и трехлитровым?

.3. Как, имея два сосуда емкостью 9л и 5л, набрать из водоема ровно 3 литра воды?

.4. Бидон, емкость которого 10 литров, наполнен соком. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить сок в два сосуда по 5 литров каждый?

.5. Имеются два сосуда. Емкость одного из них 9л, а другого 4л. Как с помощью этих сосудов набрать из бака 6 литров некоторой жидкости? (Жидкость можно сливать обратно в бак).

2.2 Методические рекомендации по использованию составленной системы задач
Эффективность системы нестандартных задач в значительной мере зависит от степени творческой активности учеников при их решении.

Собственно, одно из основных назначений системы нестандартных задач и заключается в том, чтобы активизировать мыслительную деятельность учеников на уроке [22, с 12-15].

Нестандартные задачи должны, прежде всего, будить мысль учеников, заставлять ее работать, развиваться, совершенствоваться. Говоря об активизации логического мышления учеников, нельзя забывать, что при решении нестандартных задач учащиеся не только выполняют построения, преобразования и запоминают формулировки, но и обучаются четкому логическому мышлению, умению рассуждать, сопоставлять и противопоставлять факты, находить в них общее и различное, делать правильные умозаключения.

Эффективность учебной деятельности по развитию логического мышления во многом зависит от степени творческой активности учащихся при решении системы нестандартных задач. Система нестандартных задач, должны активизировать мыслительную деятельность школьников.

Обучение на данных уроках ориентировано на развитие логического мышления ученика - он выступает в роли исследователя, творца, учитель - в роли невидимого руководителя. Обучая ребят по данному методу, можно выявить следующие изменения в личности школьника, а именно:

- у учащихся (в соответствии с возможностями каждого) развивается логическое мышление, воображение, устная речь;

дети учатся творчески выполнять любую поставленную учебную задачу;

проявляется интерес к математике.

Итак, задача учителя во время любого этапа урока заинтересовать детей к решению нестандартных задач. Развить логическое мышление, побудить их творчески мыслить, вызвать азарт решения нестандартной задачи; показать красоту именно сложного задания и, конечно же, обеспечить ситуацию успеха.

С целью его реализации нами было предложено в классическую структуру урока по математике включить следующие этапы:

1) активизацию процессов внимания и восприятия;

2) актуализацию логической операции посредством памяти, восприятия, представления;

) получение целостного представления об исследуемом математическом объекте;

) выявление алгоритма решения нестандартной задачи;

) закрепление материала;

) контроль полученных знаний.

На первом этапе использовались задания, направленные на развитие мыслительной операции. В течение 5-8 минут проводился устный счет, в который включались нестандартные задачи на развитие логического мышления, это было последовательное выполнение действий, решение устных нестандартных задач.

На втором этапе учащимся предлагалась конкретная нестандартная задача, решение которой должно быть выполнено на уроке. Ведущая роль при актуализации логической мыслительной деятельности здесь принадлежит учителю. В зависимости от поставленной цели, он формулирует и задает вопросы по условию задачи. Причем вопросы составляются таким образом, чтобы направить мышление ребенка на верный ход решения нестандартной задачи.

На третьем этапе происходит решение поставленной задачи. Ведущая роль здесь принадлежит учащимся. Учитель лишь определенным образом координирует их деятельность, направляя рассуждение детей с помощью наводящих вопросов. На этом этапе использовались преимущественно групповые формы работы и работа у доски.

На четвертом этапе выявление алгоритма решения математической задачи осуществляется путем «проигрывания» в уме конкретных действий и манипуляции с объектами, которые осуществлялись на третьем этапе развития логической операции. Ведущая роль здесь принадлежит учителю, основная форма работы - фронтальная беседа.

На пятом этапе происходит закрепление материала. Класс разбивался на несколько групп, каждая отдельно решала нестандартную задачу, а затем решения сравнивались; разбор решения нестандартной задачи у доски с комментированием и т.п.

На шестом этапе текущий контроль усвоения знаний осуществлялся на всех уроках посредством индивидуального контроля, взаимопроверки учащихся, проведения соревнований между группами по решению задач. На некоторых уроках проводились самостоятельные работы.

Включение в классическую структуру урока описанных выше этапов выполняет две взаимосвязанные функции. Во-первых, они побуждают учителя на каждом уроке по математике акцентировать свою деятельность на развитии логических мышлений учащихся, а не только обучать решению типовых задач по алгоритму; во-вторых, требуют от него применения специально разработанных методик развития логического мышления. Включая ее в практику деятельности педагога, исходили из того, что абстрактно-логическое мышление развивается из интеллектуальных операций, первоначально имеющих форму внешних предметных действий, связанных с чувственной практикой ребенка.

Реализация последующих педагогических условий: обеспечение мотивации учащихся к освоению логических операций, деятельностный и личностно ориентированные подходы к развитию логического мышления, вариативности занятий - обеспечивалась в комплексе с рассмотренным педагогическим условием, применением активных игровых методов обучения, использованием на уроках большого числа нестандартных задач.

В системе нестандартных задач были представлены различные учебные задачи, в процессе выполнения которых учащиеся учатся наблюдать, подмечать сходства и различия, замечать изменения, выявлять причины этих изменений, их характер и на этой основе делать выводы и обобщения.

Выбор системы нестандартных задач в качестве экспериментального материала для формирования приёмов и развития логического мышления школьников 5-6-х классов был обусловлен рядом причин. Во-первых, процесс их решения, как отмечают многие авторы по общему характеру вполне совпадает с процессом решения настоящих творческих задач в науке и технике. «Решая научную проблему, - пишет Л.М. Пихтарников [70, с.З], -исследователь обычно имеет какое-то количество фактов, по которым он не может сделать определённого заключения. В связи с этим исследователь выдвигает гипотезы и проверяет их справедливость, сопоставляя с имеющимися фактами... Почти так же приходится вести поиск решения нестандартной задачи. Поэтому навыки в решении нестандартных задач будут полезны каждому независимо от того, какую специальность» выберут ученики после окончания школы.

Исходя из выше сказанного, разработаны методические рекомендации по использованию нестандартных задач на уроках математики с целью развития логического мышления учащихся:

1. В целях совершенствования преподавания математики целесообразна дальнейшая разработка новых методик использования нестандартных задач на уроках математики;

2. Систематически использовать на уроках нестандартные задачи, способствующие у учащихся развитие логического мышления.

. Осуществляя целенаправленное обучение школьников решению нестандартных задач, с помощью специально подобранных систем задач, учить их наблюдать, пользоваться аналогией, индукцией, сравнениями и делать соответствующие выводы.

. Целесообразно использование на уроках задачи на смекалку, на переливание, занимательные задачи, комбинаторные задачи, логические квадраты.

. Учитывать индивидуальные особенности школьника, дифференциацию познавательных процессов у каждого из них, используя нестандартные задачи различного типа.

6. Важно, чтобы учащиеся решали не конкретную задачу, а искали общий принцип решения нестандартных задач данного вида.

7. На уроке необходима специальная деятельность школьников, направленная на выяснение сути встречаемых в условии нестандартных задач понятий и отношений. Экспериментальное обучение показало, что без понимания сути последних невозможно успешно решить нестандартную задачу.

8. При обучении необходимо так организовать учебную деятельность школьников, чтобы они сами “открывали” способы решения нестандартных задач и принципы их построения. При этом нужно рассматривать с учащимися все предложенные ими идеи и отбрасывать лишь те, которые не имеют “рационального зерна”.

9. Необходимо, чтобы учащиеся не только осознавали способ решения нестандартной задачи, но и понимали принцип его построения, а также старались осознавать основание своих действий.

На уроках математики следует уделять большое внимание решению системы нестандартных задач. Прежде всего, чтобы обучение решению нестандартных задач было успешным, учитель должен сам разобраться с задачей, изучить методику работы.

Способы решения комбинаторных задач.

Включение комбинаторных задач в средний курс математики оказывает положительное влияние на развитие логического мышления школьников. «Целенаправленное обучение решению комбинаторных задач способствует развитию такого качества математического мышления, как вариативность. Под вариативностью мышления мы понимаем направленность мыслительной деятельности ученика на поиск различных решений задачи в случае, когда нет специальных указаний на это».

Комбинаторные задачи можно решать различными методами. Условно эти методы можно разделить на «формальные» и «неформальные». При «формальном» методе решения нужно определить характер выбора, выбрать соответствующую формулу или комбинаторное правило (существуют правила суммы и произведения), подставить числа и вычислить результат. Результат - это количество возможных вариантов, сами же варианты в этом случае не образовываются.

«При отборе комбинаторных задач нужно обращать внимание на тематику и форму представления этих задач. Мы старались, чтобы задачи не выглядели искусственным, а были понятны и интересны детям, вызывали у них положительные эмоции. Желательно, для составления задач использовать практический материал из жизни».