Курсовая. kursovaya.Айгул. Методические рекомендации по изучению темы Четырехугольники План конспект урока на тему Прямоугольник Заключение
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
Тематическое планирование, 2 часа в неделю
Материал в учебнике по данной теме представлен в V главе «Четырёхугольники», которая содержит три параграфа. Каждый параграф содержит теоретический материал, который разбивается на небольшие смысловые порции, что позволяет ученику лучше осознать и выучить теоретический материал по данной теме. После изучения каждого параграфа идёт система задач различной степени трудности на закрепление изученного материала, а после изученной главы идёт система упражнений и вопросов на отработку знаний, умений и навыков. Дан образец решения задач на доказательство (№378, №384), доказана теорема Фалеса (задача №385), дано решение задач на построение 393 а), 396, даны чертежи ко всем этим задачам. Названия пунктов выделены другим цветом. Материал для заучивания (понятия, определения, формулировки теорем) выделен жирным тёмным цветом. Имеются рисунки и чертежи для наглядного представления теоретического материала, дано доказательство всех свойств и признаков рассматриваемых фигур. Изучение четырехугольников в учебнике Л. С. Атанасяна идет по следующей схеме: 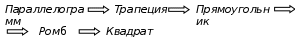 Классификация Параллелограмм Определение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. Свойства параллелограмма: 1˚ В параллелограмме противоположные стороны равны и противоположные углы равны. 2˚ Диагонали параллелограмма точкой пересечения делятся пополам. Признаки параллелограмма: 1˚ Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм. 2˚ Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. 3˚ Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм. Задачи из учебника 371. Докажите, что выпуклый четырехугольник АВСD является параллелограммом, если: а) ∠ВАС =∠АСD и ∠ВСА =∠DАС; б) АВ || СD, ∠A=∠C. 373. Периметр параллелограмма АВСD равен 50 см, ∠С=30˚, а перпендикуляр ВН к прямой CD равен 6,5 см. Найдите стороны параллелограмма. 375. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см. 376. Найдите углы параллелограмма АВСD, если: а) ∠ А = 84˚; б) ∠А - ∠В = 55˚; в) ∠А +∠С = 142˚; г) ∠А=2∠В; д) ∠САD=16˚, ∠АCD = 37˚. 380. На сторонах АВ, ВС, СD и DA четырехугольника АВСD отмечены соответственно точки M, N, P и Q так, что АМ = СР, ВN = DQ, BM = DP, NC = QA. Докажите, что четырехугольник АВСD и MNPQ – параллелограммы. 382. Диагонали параллелограмма АВСD пересекаются в точке О. Докажите, что четырехугольник А1В1С1D1, вершинами которого являются середины отрезков ОА, ОВ, ОС и ОD, - параллелограмм. Задачи из ОГЭ №1. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC = 34.  Решение: По определению параллелограмма ВС || АD, АЕ — секущая при параллельных прямых, следовательно, углы ВЕА и ЕАD равны как накрест лежащие. Поскольку ∠ВЕА=∠ВАЕ, треугольник АВЕ — равнобедренный, откуда АВ=ВЕ. Аналогично, треугольник СЕD —равнобедренный и ЕС=СD. Стороны АВ и СD равны, как противоположные стороны параллелограмма, следовательно: 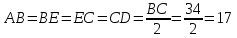 . .Ответ: 17. №2. В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.  Решение: Прямоугольные треугольники ABE и CDF равны по гипотенузе и острому углу (AB = CD как противолежащие стороны параллелограмма; ∠BAE = ∠DCF как накрест лежащие углы при параллельных прямых AB и CD и секущей AC). Следовательно, BE = DF. Кроме того, BE || DF, т. к. это перпендикуляры к одной прямой. Таким образом, в четырёхугольнике BFDE противолежащие стороны равны и параллельны, поэтому BFDE — параллелограмм. Трапеция Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны – боковыми сторонами. Трапеция называется равнобедренной, если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Задачи из учебника 386. Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции. 387. Найдите углы В и D трапеции АВСD с основаниями АD и BC, если ∠А=36˚, ∠С=117˚. 388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равны; б) диагонали равны. 390. Один из углов равнобедренной трапеции равен 68˚. Найдите остальные углы трапеции. 392. Основания прямоугольной трапеции равны а и b, один из углов равен α. Найдите: а) большую боковую сторону трапеции, если а=4 см, b=7 см, α=60˚; б) меньшую боковую сторону трапеции, если а=10 см, b=15 см, α=45˚. 397. Постройте равнобедренную трапецию АВСD: а) по основанию АD, углу А и боковой стороне АВ; б) по основанию ВС, боковой стороне АВ и диагонали BD. Задачи из ОГЭ №1. Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD = 44, BC = 24, CF:DF = 3:1 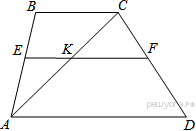 Решение: Проведём построения и введём обозначения как показано на рисунке. Рассмотрим треугольники KFC и ACD, угол C — общий, углы CAD и CKF равны друг другу как соответственные углы при параллельных прямых, следовательно, треугольники KFC и ACD подобны. Откуда  поэтому KF= поэтому KF=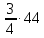 =33. Аналогично, из треугольников EKA и ABC получаем, что EK=BC =33. Аналогично, из треугольников EKA и ABC получаем, что EK=BC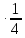 =24 =24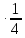 =6. =6. Таким образом, EF=EK+KF=6+33=39. Ответ: 39. №2. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 20, BF = 15.  Решение: Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, значит, 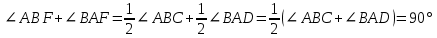 . .Получаем, что треугольник ABF прямоугольный с прямым углом F. По теореме Пифагора находим AB: 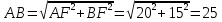 . .Ответ: 25. Прямоугольник Определение. Прямоугольником называется параллелограмм, у которого все углы прямые. Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма: в прямоугольнике противоположные стороны равны, а диагонали точкой пересечения делятся пополам. Особое свойство прямоугольника: Диагонали прямоугольника равны. Признак прямоугольника: Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. Задачи из учебника 399. Докажите, что параллелограмм, один из углов которого прямой, является прямоугольником. 401. Найдите периметр прямоугольника АВСD, если биссектриса угла А делит: а) сторону ВС на отрезки 45,6 см и 7,85 см; б) сторону DC на отрезки 2,7 дм и 4,5 дм. 402. Диагонали прямоугольника АВСD пересекаются в точке О. Докажите, что треугольники АОD и АОВ равнобедренные. 403. В прямоугольнике АВСD диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если 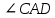 =30˚, АС = 12 см. =30˚, АС = 12 см.Задачи из ОГЭ №1. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник. Решение: Треугольники BEC и AED равны по трём  сторонам. Значит, углы CBE и DAE равны. Так как их сумма равна 180°, то углы равны 90°. Такой параллелограмм — прямоугольник. сторонам. Значит, углы CBE и DAE равны. Так как их сумма равна 180°, то углы равны 90°. Такой параллелограмм — прямоугольник.Ромб Определение. Ромбом называется параллелограмм, у которого все стороны равны. Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма. Особое свойство ромба: Диагонали ромба взаимно перпендикулярны и делят Задачи из учебника 405. В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы, которые диагонали ромба образуют с его сторонами. 406. Найдите периметр ромба АВСD, если 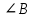 =60˚, АС=10,5 см. =60˚, АС=10,5 см.402. Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 45˚. 403. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ параллелограмма является биссектрисой его угла. 433. Из вершины В ромба АВСD проведены перпендикуляры ВК и ВМ к прямым AD и DC. Докажите, что луч ВD является биссектрисой угла КВМ. 434. Докажите, что точка пересечения диагоналей ромба равноудалена от его сторон. Задачи из ОГЭ №1. Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 1. Найдите высоту ромба. 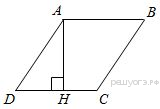 Решение: Поскольку ABCD — ромб, AD = DC = DH + HC = 13. Треугольник ADH прямоугольный, поэтому: АН= 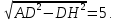 №2. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба. В ответе запишите величины различных углов в порядке возрастания без пробелов. 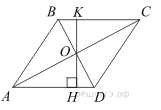 Введём обозначения, как показано на рисунке. Пусть диагональ АС равна 76. Диагонали ромба пересекаются под прямым углом и делятся точкой пересечения пополам. Рассмотрим треугольник АОН, он прямоугольный, найдём синус угла ОАН: sin 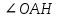 = =  , следовательно, угол OAH равен 30°. , следовательно, угол OAH равен 30°.Рассмотрим треугольники AOB и AOD, они прямоугольные, AO — общая, AB=AD, следовательно, эти треугольники равны, откуда ∠ВАO =∠OAD=30˚, поэтому ∠BAD=2∙30˚=60˚. Сумма смежных углов ромба равна 180˚, откуда ∠AВС=180˚-∠BAD=180˚-60˚=120˚. Ответ: 60120 Квадрат Определение. Квадратом называется прямоугольник, у которого все стороны равны. Прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом. Отсюда следует, что квадрат обладает всеми свойствами прямоугольника и ромба. Основные свойства квадрата: Все углы квадрата прямые. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. | |||||||||||||||||||||||
