Курсовая. kursovaya.Айгул. Методические рекомендации по изучению темы Четырехугольники План конспект урока на тему Прямоугольник Заключение
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
Задачи из учебника 409. Докажите, что ромб, у которого один угол прямой, является квадратом. 410. Является ли четырехугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину? 411. В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырехугольник – квадрат. 415. Постройте квадрат: а) по стороне; б) по диагонали. 436. Диагональ АС квадрата АВСD равна 18,4 см. Прямая, проходящая через точку А и перпендикулярная к прямой АС, пересекает прямые ВС и СD соответственно в точках М и N. Найдите МN. Задачи из ОГЭ №1. Найдите площадь квадрата, описанного вокруг окружности радиуса 39. Решение: Сторона квадрата равна диаметру вписанной в него окружности, значит площадь данного квадрата равна: 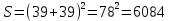 Ответ: 6084 №2. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры. 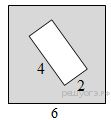 Решение: Площадь получившейся фигуры равна разности площадей квадрата и прямоугольника: 6 · 6 − 4 · 2 = 28. Ответ: 28. Описанные и вписанные четырехугольники (Глава VIII §4) Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник. В отличие от треугольника не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник, не являющимся квадратом, можно «поместить» окружность, касающуюся трех его сторон, но нельзя вписать окружность. Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством: В любом описанном четырехугольнике суммы противоположных сторон равны. Верно и обратное утверждение.  Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности. Очевидно, эта окружность будет называться описанной вокруг четырехугольника. В отличие от треугольника около четырехугольника не всегда можно описать окружность. Например, нельзя описать окружность около ромба, не являющегося квадратом. Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством: В любом вписанном четырехугольнике сумма противоположных углов равна 180˚. Верно и обратное утверждение. 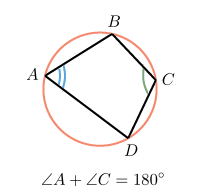 Задачи из учебника 695. Сумма двух противоположных сторон описанного четырехугольника равна 15 см. Найдите периметр этого четырехугольника. 696. Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб. 698. Сумма двух противоположных сторон описанного четырехугольника равна 12 см, а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника. 708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любой равнобедренной трапеции. 709. Докажите, что если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник. 710. Докажите, что если около трапеции можно описать окружность, то эта трапеция – равнобедренная. Задачи из ОГЭ №1. В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ = 14, SQ = 4. 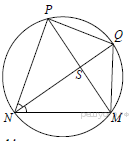 Решение: Поскольку ∠QPS = ∠QPM = ∠MNQ = ∠QNP (см. рис.), треугольник PQS подобен треугольнику NQP по двум углам (угол при вершине Q общий). Поэтому 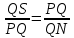 . Пусть NS = x. Тогда . Пусть NS = x. Тогда 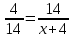 . . Из этого уравнения находим, что x = 45. Ответ: 45. №2. Диагонали четырёхугольника АВСD, вершины которого расположены на окружности, пересекаются в точке М. Известно, что ∠АВС = 72°, ∠ВСD = 102°, ∠AMD = 110°. Найдите ∠ACD.  Решение: Пусть ∠АСD = x. ∠DMC = 180˚-110°=70˚; ∠DMC = ∠DBC+∠BCA; ∠BCA=102˚-x; ∠DBC+102˚-x =70˚; x=∠DBC+32˚. ∠DBC+∠ABD=72˚; ∠ABD=x; ∠DBC=72˚-x; 2x=104˚; x=52˚. Ответ: 52˚ №3. Два угла вписанного в окружность четырехугольника равны 82˚ и 58˚. Найдите больший из оставшихся углов. Ответ дайте в градусах. 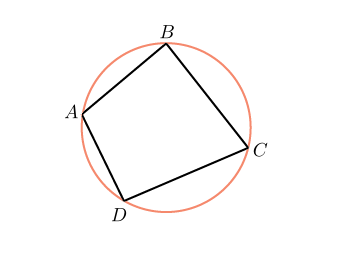 Решение: Сумма противоположных углов вписанного четырехугольника равна 180˚. Пусть угол А равен 82˚. Тогда напротив него лежит угол в 98 градусов. Если угол В равен 58˚, то угол D равен 180˚-58˚=122˚. Ответ:122. №4. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию. 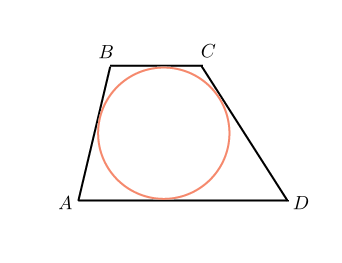 Решение: Мы помним, что средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны a и с, а боковые стороны — b и d. По свойству описанного четырехугольника, a+c=b+d, и значит, периметр равен 2(a+c). Получаем, что a+c=20, а средняя линия равна 10. Ответ: 10. №5. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:2:3. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 32. 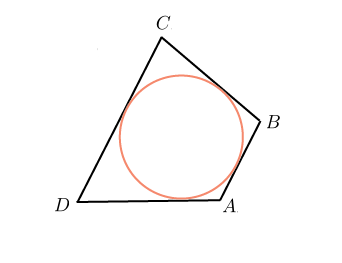 Решение: Пусть сторона АВ равна х, АD равна 2x, а DC - 3x. По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит, х+3х=ВС+2х. Получается, что BC равна 2х. Тогда периметр четырехугольника равен 8х. Мы получаем, что х=4, а большая сторона равна 12. Ответ: 12. План – конспект урока на тему «Прямоугольник» Цель урока: -рассмотреть свойства и признаки прямоугольника как частного случая параллелограмма, сформулировать и доказать его особые свойства и признаки, формировать умения решать задачи с применением доказанных теорем. -развивать логическое мышление учащихся, умение грамотно выполнять и читать чертежи, математическую речь, интерес к предмету. -воспитывать дисциплинированность, ответственное отношение к учебному труду. Задачи урока: -Повторить понятия прямоугольника, опираясь на полученные знания в курсе математики 1-6 классе; -Рассмотреть свойства и признак прямоугольника через элемент исследования; -Научить обучающихся, применять свойства в процессе решения задач; -Рассмотреть задачи, развивающие компетентности ученика. Оборудование: ПК, проектор, экран, презентация. Тип урока: урок изучения и закрепление новых знаний. Ход урока 1.Организационный момент. Добрый день ребята! Я рада видеть вас на нашем уроке. Надеюсь мы с вами сегодня хорошо поработаем. Садитесь. 2. Мотивация урока. " Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг - геометрия". Эти слова, сказанные великим французским архитектором Ле Корбюзье, в начале ХХ века очень точно характеризуют и наше время. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нем, открывать новое, понимать красоту и мудрость окружающего мира поможет вам эта наука. Сегодня на уроке каждый оценит свою работу и выставит себе баллы в оценочный лист. • правильно выполненное задание – 3 балла • ошибки при выполнении задания – 2 балла • невыполнение задания – 0 баллов. 3. Актуализация опорных знаний. Проверка д/з. Геометрия в 8 классе началась с главы «Четырехугольник». Это одна из важных тем, которая широко используется при решении задач на ОГЭ и ЕГЭ. Проверка домашнего задания. - Какая фигура называется четырехугольником? - Назовите виды четырехугольников, которые изучили? - Дайте определение трапеции. Какие бывают трапеции. Определение равнобедренной, прямоугольной трапеции. - Дайте определение параллелограмма. - Каким свойством обладают противоположные стороны параллелограмма? - Каким свойством обладают противоположные углы параллелограмма? - Каким свойством обладают диагонали параллелограмма? - Сформулируйте признаки равенства прямоугольных треугольников? Решение задач на готовых чертежах.  4.Изучение нового материала. В жизни нет важней фигуры! Прямоугольник всюду есть. С ним любые процедуры Угол равен, ему – честь! Дом и Стол, тетрадь и книжка Прямоугольника пример… Без фигуры этой – крышка!шо Не построишь – мерь, не мерь! Запишите число и тему урока. 1.Ввести понятие прямоугольник. Среди предложенных четырехугольников выбрать те, которые являются прямоугольником. Давайте будем разбираться с данной фигурой. Каково взаимное расположение противоположных сторон прямоугольника? Верно, они попарно параллельны. А мы уже встречались с фигурой, у которой противоположные стороны попарно параллельны, как называется такая фигура? Правильно параллелограмм! Какой мы можем сделать вывод о прямоугольнике? Как можно назвать прямоугольник? Да. Прямоугольник - это параллелограмм. А что его отличает от параллелограмма? У него все углы прямые, т. е. равны. А у параллелограмма только противоположные углы равны. Закончите предложение: «Прямоугольник-это параллелограмм, у которого…….» 2.Рассмотреть особое свойство диагоналей прямоугольника. Так как прямоугольник – это параллелограмм, то какими свойствами он обладает? Ответим на этот вопрос, исследуйте стороны, углы и диагонали прямоугольника и заполните таблицу на рабочих листах
Каким отличительным свойством он обладает? 3.Свойства прямоугольника. Диагонали прямоугольника равны. 1)Рассмотрим Δ ACD и Δ DBA AD-общая AB=CD, т. к. ABCD-параллелограмм 2) Значит ΔACD= ΔDBA по 2 катетам. 3) Значит AC=BD, как соотв. элементы в равных треугольниках. Теорема доказана. 4.Рассмотреть признак треугольника. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. Доказательство: AC=BD (по условию), тогда ΔACD = Δ ABD по3 сторонам(AD- общая сторона, AB = CD, AC=BD) ∟A= ∟D - как соответственные элементы ∟A=∟C, ∟B= ∟D, т. к. в параллелограмме противоположные углы равны; ∟A= ∟D= ∟C= ∟B 4) ∟A+∟B+ ∟C+ ∟D= 3600 следовательно,∟A= ∟B= ∟C= ∟D=900 5) Значит ABCD- прямоугольник. Теорема доказана. Оцените свою работу 5.Закрепление изученного материала Решение задач на готовых чертежах.  Решение задачи № 403 у доски. Дано: ABCD – прямоугольник, AC ∩ BD = O, Найти: P AOB 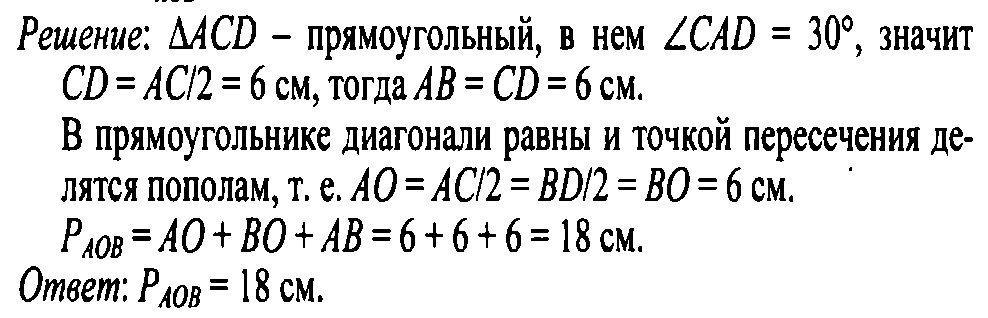 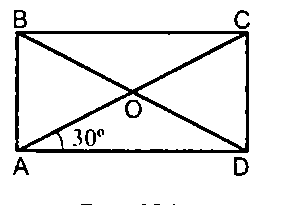 Оцените свою работу 5.Контроль знаний Впишите пропущенные слова. Прямоугольником называется _____, у которого все углы _____. Свойство прямоугольника: _____ прямоугольника равны. Признак прямоугольника: если в параллелограмме диагонали _____, то этот параллелограмм – _____. Оцените свою работу 6.Итог урока. Домашнее задание п.45, вопросы 12,13 стр. 115, № 399, № 401 (а). Рефлексия. Мы знаем, что диагонали параллелограмма точкой пересечения длятся пополам. Применим это свойство для получения оценки за урок. Посчитайте итоговое количество набранных баллов и разделите на 2. Если вы набрали 10-13 баллов, ваша оценка «5» Если вы набрали 7-9 баллов, ваша оценка «4» Если вы набрали 5-7 баллов, ваша оценка «3» Трудным ли для тебя был материал урока? На каком из этапов урока было труднее всего, легче всего? Что нового ты узнал на уроке? Чему научился? Работал ли ты на уроке в полную меру сил? Как эмоционально ты чувствовал себя на уроке? |
