Теоретическая механика. ТеорМех. Примеры. Методические рекомендации по решению задач

• Название: Методические рекомендации по решению задач
• Анкор: Теоретическая механика
• Дата: 20.10.2020
• Размер: 317.36 Kb.
• Имя файла: ТеорМех. Примеры.docx
• Тип: Методические рекомендации; #144413
• страница: 2 из 3

Пример 13. С воздушного шара, опускающегося вниз с постоянной скоростью 2 м/с, бросили вертикально вверх груз со скоростью 18 м/c относительно земли. Определить расстояние между шаром и грузом в момент, когда груз достигает высшей точки своего подъема. Через какое время груз пролетит мимо шара, падая вниз.

Дано: v₀₁= 2 м/с, v₀₂=18 м/c

Найти: s-?  τ -?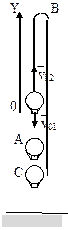



Решение. Направим ось 0Y вертикально  вверх, начало совместим с точкой 0, в которой находился шар в момент бросания груза.    

Тогда уравнения движения груза  и воздушного шара:



Скорость движения груза изменяется по закону v₂=v₀₂ – gt.

В наивысшей точке В подъема груза v₂=0. Тогда  время подъема до этой точки   Координата груза в точке В



За это время воздушный шар опустился до точки А; его координата  



Расстояние между точками А и В: 



Через промежуток времени τ, когда камень пролетит мимо шара, координаты тел будут одинаковы: у_1С=у_2С;     



Отсюда



 

Пример 14. С какой скоростью и по какому курсу должен лететь самолет, чтобы за два часа пролететь на север 300 км, если во время полета дует северо-западный ветер под углом 30^о к меридиану со скоростью 27 км/ч?

Дано: t=7,2∙10³ c;   l=3∙10⁵ м;   α=30° ≈ 0,52 рад;   v₂ ≈7,2 м/с.

Найти: v₂ -?   φ -?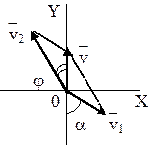



Решение. Рассмотрим движение самолета в системе отсчета, связанной с землей.

Проведем ось ОХ в направлении на восток, а ось OY - на север. Тогда скорость движения самолета в выбранной системе отсчета

                                     (1)

где  v=l/t                                        (2)

Уравнение (1) в проекции на оси

ОХ: 0=v₁∙sinα – v₂∙sinφ;

OY: v= v₂∙cosφ - v₁∙cosα, или   v₁∙sinα = v₂∙sinφ,          v₂∙cosφ=v₁∙cosα + v                 (3)

Разделив  эти уравнения почленно, получим tgφ=v₁sinα/(v₁cosα+ v),  

или с учетом (2)            

tgφ=v₁∙sinα/(v₁∙cosα+ l/t);

φ=arctgv₁∙sinα/(v₁∙cosα+ l/t) ≈0,078 рад.

Возводя в квадрат правые и левые части уравнений (3) и складывая полученные уравнения, находим 

v₂²∙sin²φ + v₂² ∙cos²φ = v₁² sin²α+ (v₁∙cosα + v)²,

откуда  , или с учетом (2)



 

Пример 15. Тело, брошенное вертикально вверх, вернулось на землю через t=3 с. Найти высоту подъема тела и его начальную скорость.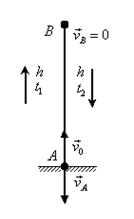



Решение. Движение тела вверх является равнозамедленным с ускорением - g и происходит в течение времени t₁, а движение вниз – равноускоренным с ускорением g и происходит в течение времени t₂.  Уравнения, описывающие движение на участках АВ и ВА, образуют систему: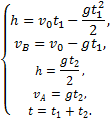 



Поскольку v_B=0, то v₀=gt₁. Подставив v₀ в первое уравнение системы, получим  . Если сравнить это выражение с третьим уравнением системы, то можно сделать вывод о том, что время подъема равно времени спуска t₁=t₂=t/2=1,5с. Начальная скорость и скорость при приземлении равны друг другу и составляют v₀=v_A=gt₁=9,8∙1,5=14,7 м/с.

Высота подъема тела



 

Пример 16. Свободно падающее тело в последнюю секунду движения прошло половину пути. Найти высоту, с которой оно брошено и время движения.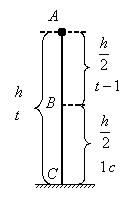



Решение. Зависимость пройденного пути от времени для свободно падающего тела  . Поскольку участок ВС, составляющие половину всего пути,  пройден за время, равное 1 с, то первая половина пути АВ пройдена за время (t-1) с. Тогда движение на участке ВС может быть описано как  .  

 Решая систему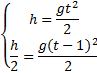



получим t²-4t+2=0. Корни этого уравнения t₁=3,41 с и t₂=0,59 с. Второй корень не подходит, т.к. время движения, исходя из условия задачи, должно превышать одну секунду. Следовательно,  тело падало в течение 3,41 с и прошло за это время путь   

 

Пример 17. С башни высотой 25 м горизонтально брошен камень со скоростью 15 м/с.

Найти: 1) сколько времени камень будет в движении, 2) на каком расстояниион упадет на землю, 3) с какой скоростью он упадет на землю, 4) какой угол составит траектория камня с горизонтом в точке его падения на землю. Сопротивление воздуха не учитывать.

Дано: Н=25 м, v_o=15 м/с

Найти: t-?  s_x- ?  v - ? φ- ?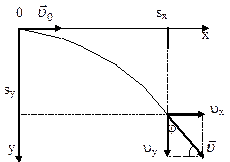



 

Решение. Перемещение брошенного горизонтально камня можно разложить на два: горизонтальное s_x и вертикальное s_y:

s_y=H=gt²/2,    

 s_x=v_ot, 

где t - время движения.

Отсюда: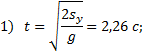    



2)  s_x=v_ot= 33,9 м;        

3)  v_y=gt=22,1м/с;

4)  sinφ= v_y/v=0,827;          

φ=55^о48’.

 

Пример 18. С башни высотой 25 м горизонтально со скоростью v_x=10 м/c брошено тело.

Найти: 1) время t падения тела, 2) на каком расстоянии l от основания башни оно упадет, 3) скорость v в конце падения, 4) угол, который составит траектория тела с землей в точке его приземления.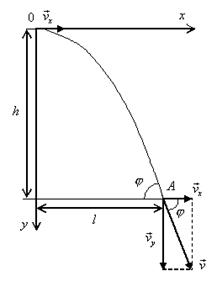



Решение. Движение тела является сложным. Оно участвует в равномерном движении по горизонтали и равноускоренном с ускорением g по вертикали. Поэтому участок АВ описывается уравнениями: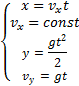



Для точки А эти уравнения принимают вид: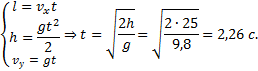



Тогдаl=10∙2,26=22,6 м, а v_y=9,8∙2,26=22,15 м/с.

Поскольку  , то  

Угол, который траектория составляет с землей, равен углу φ в треугольнике скоростей в  т. А, тангенс которого   , поэтому φ=68,7°.

 

Пример 19. Для тела, брошенного с горизонтальной скоростью v_x=10 м/с, через время t=2 с после начала движения найти: нормальное, тангенциальное и полное ускорения, а также радиус кривизны траектории в этой точке.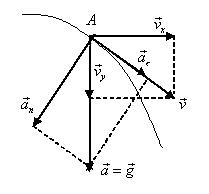



Решение. Вертикальная составляющая скорости v_y=gt=9,8∙2=19,6 м/с

Скорость в точке А:

, то  

Векторы   образуют треугольник скоростей, а векторы   - треугольник ускорений. Как видно из рисунка, эти треугольники подобны, а это означает, что их стороны пропорциональны:  .

Отсюда,  





Нормальное ускорение  , поэтому радиус кривизны траектории



 

Пример 20. Мяч бросили со скоростью 10 м/с под углом 40^о к горизонту.

Найти: 1) на какую высоту поднимется мяч; 2) на каком расстоянии от места бросания мяч упадет на землю, 3) сколько времени он будет в движении.

Дано: v_o=10 м/с, α=40^о.

Найти: s_y - ?  s_x - ?  t - ?



Решение.  1) Найдем наибольшую высоту s_y max, на которую поднимается тело, брошенное со скоростью v_o  подуглом α к горизонту. Имеем (см. рис.):               

v_y=v_o sinα – gt;                         (1)

s_y=v_ot∙sinα – gt²/2.                    (2)

В верхней точке v_y=0  и из (1) получим v_o∙sin𝛼 = gt₁, отсюда время подъема мяча t₁=v_o∙sinα/g. Подставляя t₁ в (2), получим

s_y max= v_o² ∙sin²α/(2g)= 2,1 м.

2) Найдем дальность полета s_x max  тела, брошенного под углом к горизонту.

Имеем: v_x=v_o∙cosα,                 (3)

s_x=v_xt=v_ot∙cosα.                    (4)

Тело упадет на горизонтальную плоскость через время t₂=2t₁=2v_osinα/g.

Подставляя t₂ в (4), получим  s_xmax = v_о²sin2α/g=10,0 м.

3) t₂=2t₁=2v_osinα/g=1,3 с.

 

Пример 21. Тело брошено со скоростью v₀=10 м/с² под  углом α=30° к горизонту. На какую высоту  тело поднимется. На каком расстоянии от места бросания оно упадет на землю? Какое время он будет в движении?



Решение. Горизонтальная и вертикальная составляющие начальной скорости





Движение на участке ОА можно разложить на два простых движения: равномерное по горизонтали и равнозамедленное по вертикали:



В точке А      



Тогда    и     

Если тело участвует одновременно в нескольких движениях, то в каждом из них оно участвует независимо от другого, следовательно, время движения на участке АВ определяется временем движения вниз – t₂. Время движения вверх равно времени движения вниз, а,  значит,   

При равномерном движении по горизонтали за равные промежутки времени тело проходит равные участки пути, следовательно,



Дальность полета



Высота подъема тела



 

Пример 22. Точка движется прямолинейно на плоскости по закону x=4(t-2)². Каковы начальная скорость v₀ и ускорение точки a? Найти мгновенную скорость точки v_t=5 в начале пятой секунды движения.

Решение.

1) Т.к. v=x’,  то  v₀=(4∙(t-2)²)’=(4∙(t²-4t+4))’=(4t²-16t+16)’=8t-16

       при t=0     v₀=-16 м/с.

2) Т.к. a= , то a=(8t-16)’=8 м/с.

3) При t=4, т.к. до начала 5 с прошло 4 с.

   v_t=5=8t-16=8∙4-16=32 м/с.

Ответ: Начальная скорость точки v₀=-16 м/с, ускорение a=8 м/с, скорость точки в начале пятой секунды движения v_t=5=32 м/с.

 

Пример 23. Движение материальной точки описывается уравнениями: а) s=αt³; б) s=αt²+βt. Сравните среднюю скорость   и среднеарифметическую начальной и конечной скоростей v_ср в интервале времени 0 - t. Здесь α и β - положительные постоянные.

Решение. Вспомним определения средней и мгновенной скорости:



Выражения для мгновенной скорости получаются путем дифференцирования уравнения движения.



Выражения для средней скорости находятся как отношение изменения криволинейной координаты к времени:



Получим выражения для среднеарифметической скорости:



Ответим на вопрос условия задачи. Видно, что в случае “а” средняя и среднеарифметическая скорости не совпадают, а в случае “б” - совпадают.

 

Пример 24. Материальная точка движется равномерно по криволинейной траектории. В какой точке траектории ускорение максимально?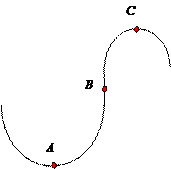



 

Решение. При движении по криволинейной траектории ускорение складывается из тангенциального и нормального. Тангенциальное ускорение характеризует быстроту изменения величины (модуля) скорости. Если величина скорости не изменяется, тангенциальное ускорение равно нулю. Нормальное ускорение зависит от радиуса кривизны траектории a_n=v²/R. Ускорение максимально в точке с наименьшим радиусом кривизны, т.е. в точке С.