Теоретическая механика. ТеорМех. Примеры. Методические рекомендации по решению задач
 Скачать 317.36 Kb.
|
|
Пример 25. Материальная точка движется согласно закону:  1) Определить начальную координату, начальную скорость и ускорение путем сравнения с законом движения с постоянным ускорением. Записать уравнение для проекции скорости. Решение. Закон движения с постоянным ускорением имеет вид  Сравнивая это уравнение с уравнением условия задачи, получаем x0 = - 1 м, v0x = 1 м/с, ax = - 0,25 м/с2. Возникает вопрос: какой смысл имеет знак “минус”? Когда проекция вектора отрицательна? Только в том случае, когда вектор направлен против оси координат. Изобразим на рисунке начальную координату, векторы скорости и ускорения.  Запишем уравнение для скорости в виде  и подставим в него полученные данные (начальные условия)  2) Найти зависимость скорости и ускорения от времени, применяя определения этих величин. Решение. Применим определения для мгновенных значений скорости и ускорения:  Производя дифференцирование, получим vx=1-0,25t, ax = - 0,25 м/с2. Видно, что ускорение не зависит от времени. 3) Построить графики vх(t) и aх(t). Охарактеризовать движение на каждом участке графика. Решение. Зависимость скорости от времени - линейная, график представляет собой прямую линию. При t = 0 vх = 1 м/с. При t = 4 с vх = 0.  Из графика видно, что на участке “а” проекция скорости положительная, а ее величина убывает, т.е. точка движется замедленно в направлении оси х. На участке “b” проекция скорости отрицательная, а ее модуль возрастает. Точка движется ускоренно в направлении, противоположном оси х. Следовательно, в точке пересечения графика с осью абсцисс происходит поворот, изменение направления движения. 4) Определить координату точки поворота и путь до поворота. Решение. Еще раз отметим, что в точке поворота скорость равна нулю. Для этого состояния из уравнений движения получаем:   Из второго уравнения получаем tпов = 4 с. (Видно, чтобы получить это значение не обязательно строить и анализировать график). Подставим это значение в первое уравнение: xпов=-1+4-42/8 = 1 м. Изобразим, как двигалась точка.  Путь до поворота, как видно из рисунка, равен изменению координаты: sпов=xпов-x0=1-(-1)=2 м. 5) В какой момент времени точка проходит через начало координат? Решение. В уравнении движения следует положить х = 0. Получаем квадратное уравнение 0=-1+t-t2/8 или t2-8t+8=0. У этого уравнения два корня:  . t1 = 1,17 с, t2 = 6,83 с. Действительно, точка проходит через начало координат два раза: при движении “туда” и “обратно”.6) Найти путь, пройденный точкой за 5 секунд после начала движения, и перемещение за это время, а также среднюю путевую скорость на этом участке пути. Решение. Прежде всего найдем координату, в которой оказалась точка после 5 секунд движения и отметим ее на рисунке. x(5)=-1+5-52/8= 0,875 м. 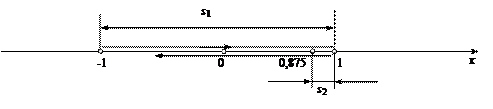 Поскольку в данном состоянии точка находится после поворота, то пройденный путь уже не равняется изменению координаты (перемещению), а складывается из двух слагаемых: пути до поворота s1 = xпов - x0 = 1 - (-1) = 2 м и после поворота s2 = xпов - x(5) = 1 - 0,875 = 0,125 м, s = s1 + s2 = 2,125 м. Перемещение точки равно sх = x(5) - x0 = 0,875 - (-1) = 1,875 м Средняя путевая скорость вычисляется по формуле  В рассмотренной задаче описан один из наиболее простых видов движения - движение с постоянным ускорением. Тем не менее, данный подход к анализу характера движения является универсальным. Пример 26. При одномерном движении с постоянным ускорением зависимости координаты и скорости частицы от времени описываются соотношениями: 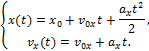 Установить связь между координатой частицы и ее скоростью. Решение. Из этих уравнений исключаем время t. Для этого используем метод подстановки. Из второго уравнения выражаем время и подставляем в первое уравнение:  Если движение начинается из начала координат (х0 =0) из состояния покоя (v0x =0), то полученная зависимость принимает вид  хорошо знакомый из школьного курса физики. Пример 27. Движение материальной точки описывается уравнением:  , где i и j - орты осей х и у, α и β - положительные постоянные. В начальный момент времени частица находилась в точке х0 =у0=0. Найти уравнение траектории частицы у(х).Решение. Условие задачи сформулировано с применением векторного способа описания движения. Перейдем к координатному способу. Коэффициенты при единичных векторах представляют собой проекции вектора скорости, а именно:  Вначале получим зависимости x(t) и y(t), решая задачу первого класса. 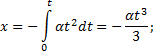 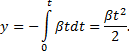   Из полученных уравнений исключим времяt. Из первого уравнения  . Из второго уравнения получаем Обратим внимание, что координата х должна быть отрицательной, что соответствует положительным значениям времени t. Пример 28. Частица движется в положительном направлении оси x так, что ее скорость меняется по закону , где α - положительная постоянная. Учитывая, что в момент времениt = 0 она находилась в начале координат (x0 = 0), найти зависимость от времени скорости частицы. Решение. Установим уравнения, связывающие v и x. По условию задачи . В тоже время можно записать . Отсюда  (ее исключить проще всего). Получилось дифференциальное уравнение с разделяющимися переменными.Разделяя переменные  и интегрируя от 0 до t и от 0 до х,  , получаем: , откуда находим зависимость координаты от времени Искомую зависимость скорости от времени можно получить, применяя любое из двух исходных уравнений. Например,  Пример 29. Частица движется в положительном направлении осиx так, что ее ускорение меняется по закону a=α-βx, где α и β - положительные постоянные. Учитывая, что в момент времени t = 0 она покоилась и находилась в начале координат (x0 = 0), найдем зависимость скорости частицы от координаты. Решение. Установим уравнения, связывающие а иx. a=α-βx, (1)   В эти три уравнения входят четыре переменных: x, v, a, t. Исключим a и t. Выразим из (2) и подставим в (3):  С учетом выражения (1) получаем дифференциальное уравнение  Разделяя переменные  и производя интегрирование 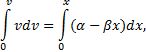 получаем  Искомая зависимость скорости от координаты имеет вид  Пример 30. С башни высотой h бросили камень со скоростью v0 под углом α к горизонту. Найти: 1) какое время камень будет в движении; 2) на каком расстоянии s он упадет на землю; 3) с какой скоростью он упадет на землю; 4) какой угол β составит траектория камня с горизонтом в точке его падения; 5) нормальное и тангенциальное ускорения камня в этой точке, а также радиус кривизны траектории; 6) наибольшую высоту подъема камня. Сопротивлением воздуха пренебречь. Решение. На примере этой задачи покажем, как в обобщенном виде можно установить приведенный алгоритм решения любой задачи данного класса. 1. В задаче рассматривается движение материальной точки (камня) в поле силы тяжести Земли. Следовательно, это движение с постоянным ускорением свободного падения g, направленным вертикально вниз. 2. Движение камня рассматривается относительно наблюдателя, находящегося на земле. Движение двумерное - по горизонтали и вертикали. Применим координатный способ описания. Начало координат поместим на поверхности земли, ось х направим горизонтально, ось у - вертикально вверх. 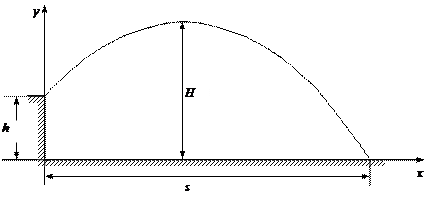 3. В условии задачи рассматривается начальное состояние, состояние А, соответствующее моменту непосредственно перед ударом камня о землю, и состояние В, соответствующее наивысшей точке траектории. Изобразим эти состояния на рисунке и нарисуем векторы скорости в каждом состоянии. Поскольку применяется координатный способ описания, каждый вектор разложим на составляющие. Как было отмечено ранее, вектор ускорения во всех состояниях одинаков и равен g.  4. Движение с постоянным ускорением описывается хорошо известными уравнениями: 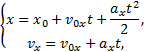 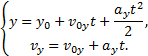 Конкретизируем их для данной задачи. По оси х камень движется из начала координат без ускорения (равномерно) со скоростью v0x. По оси y камень движется из точки с координатой h с ускорением свободного падения, направленным против оси у и с начальной скоростью v0у. Отразим эти данные в начальных условиях x0=0, v0x=v0cosα, ax=0, y0=h, v0y=v0sinα, ay=-g. и подставим их в уравнения движения. 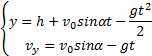  5A. Рассмотрим состояние А. В этом состоянии камень оказался спустя tA секунд после начала движения. Координаты этой точки равны хА =s, уА = 0. На рисунке указаны вектор скорости в этой точке vA (направленный по касательной к траектории) и его составляющие. Применим уравнения движения к данному состоянию:     В эти четыре уравнения входят следующие неизвестные: tA , s, vАx и vАy. 6А. Разрешим полученную систему уравнений относительно указанных неизвестных. Видно, что в уравнение (3) входит одна неизвестная величина - tA. Решим это квадратное уравнение, преобразовав его предварительно к приведенному виду: 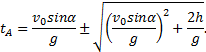  Проанализируем полученный результат. Время не может быть отрицательным, следовательно, отрицательный корень не имеет смысла. Поэтому 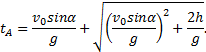 Уравнения (1), (2), (4) позволяют найти все оставшиеся величины: s, vАx и vАy. Модуль скорости выразим по теореме Пифагора  Из рисунка видно, что  Чтобы найти нормальную и тангенциальную составляющие вектора ускорения, разложим вектор g.  Из рисунка видно, что  Учитывая, что нормальное ускорение связано с модулем скорости соотношением  выразим радиус кривизны траектории в данной точке:  5В. Рассмотрим состояние В. В этом состоянии камень оказался спустя tВ секунд после начала движения. Координаты этой точки равны хВ, уВ = H. На рисунке указан вектор скорости в этой точке vВ, направленный горизонтально по оси х. Следовательно, вертикальная составляющая скорости равна нулю vВy =0. Применим уравнения движения к данному состоянию:     Время tВ найдем из уравнения (4)  а максимальную высоту подъема - из уравнения (3)   Видно, что уравнения (1) и (2) не потребовались при решении этой задачи. Пример 31. Трамвай движется прямолинейно от остановки А до следующей остановки В с ускорением, меняющимся по закону a=α-βx, где α и β - положительные постоянные, х - расстояние между трамваем и остановкой А. Найти расстояние между остановками и максимальную скорость трамвая. Решение. Решим задачу в соответствии с установленным алгоритмом. 1) Трамвай можно считать материальной точкой, которая движется по прямолинейной траектории. Отличительной чертой его движения является заданная в условии задачи зависимость ускорения от координаты. 2) Применим координатный способ описания движения. Совместим начало координат с остановкой А. Отметим положение остановки В и тоски С, в которой скорость трамвая максимальна.  3) Установим, какая информация о координатах, скоростях, ускорениях содержится в условии задачи, какую требуется определить. В начальном и конечном состояниях скорости равны нулю, а в состоянии С скорость максимальна, поэтому ускорение (производная скорости по времени) равно нулю.
4) В условии задана зависимость ускорения от координаты a=α-βx, (1) известны или требуют нахождения значения координаты и скорости в состояниях В и С. Следовательно, необходимо уравнение, связывающее v и x.  5) Применим кинематические уравнения к состоянию В. Подставим в уравнение (2) соответствующие значения координаты и скорости  Поскольку в состоянии В s≠0, то 2α-βs=0, откуда Применим кинематические уравнения к состоянию С. Подставим в уравнения (1) и (2) соответствующие значения координаты и ускорения. aC=0=α-β∙xC, (1a)  Из (1а) выразим координату точки С и подставим в уравнение (2а): 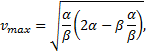 Откуда  |